User login
Number needed to treat (NNT) is a measure of clinical effect that has been called medicine’s “secret stat”(Box 1).1,2 By itself, however, the NNT provides no information about whether a trial result is probably true (statistical significance). If a NNT is statistically significant, the confidence interval (CI) can tell you the range of numbers within which the truth probably lies.
In the March 2007 issue of Current Psychiatry, we described how to use NNT to interpret and apply research data in daily practice.3 In this article, we explain the “secrets” of NNT and CI by providing sample calculations and several figures for visual learning. For illustration, we analyze data from the Clinical Antipsychotic Trials of Intervention Effectiveness (CATIE) in schizophrenia, this time focusing on phase 2E—the efficacy pathway in which patients were randomly assigned to open-label clozapine or a double-blinded second-generation antipsychotic (SGA).4
Confidence intervals: Is the NNT statistically significant?
To find out a NNT’s statistical significance, you can examine the CI. A 95% CI means that the truth lies between the interval’s lower and upper bounds with a 95% probability.
Calculating CI. Although formulas to calculate the CI appear complicated,5 they are easily inserted into a Microsoft Excel-brand spreadsheet. Useful alternatives are online calculators (seeRelated Resources), which can be downloaded to your hand-held device or pocket PC.
Time magazine recently declared NNT as medicine’s “secret stat.”1 NNT allows us to place a number on how often we would see a difference between 2 interventions.
In a handbook on essentials of evidence-based clinical practice, Guyatt et al2 define NNT as “the number of patients who must receive an intervention of therapy during a specific period of time to prevent 1 adverse outcome or produce 1 positive outcome.”
If a difference in therapeutic outcome is seen once in every 5 patients treated with 1 intervention vs another (NNT of 5), it will likely influence day-to-day practice. However, if a therapeutic difference occurs in 1 of every 100 patients (NNT of 100), the difference between 2 treatments is not usually of great concern (except, for example, in assessing immunization against a rare but very dangerous illness).
A 95% CI of 5 to 15 means we are dealing with a NNT that with 95% probability falls between 5 and 15. However, if the NNT is not statistically significant, it becomes more difficult to describe the CI.6 A non-statistically significant NNT would have a CI that includes a negative number and a positive number: When comparing intervention A with intervention B, A might be better than B or B might be better than A. One bound of the CI may be a NNT of 10 and the other may be –10. It would be tempting to describe the CI as –10 to 10, but this would be misleading.
Attributable risk. NNT is calculated by taking the reciprocal of the difference between 2 rates for a particular outcome (Box 2). This difference is known as the attributable risk (AR). We can calculate a 95% CI for the AR, and the AR is considered statistically significant if both ends of the 95% CI are positive or both ends are negative.
If the 95% CI includes zero, then the AR is considered not statistically significant.
An AR value of zero means the rates of the outcome of interest are the same for the 2 interventions (there is no difference). Translating this to NNT would mean that no matter how many patients you treat with 1 intervention versus the other, you will not see a difference on the outcome of interest. The NNT would be “infinite” (represented by the symbol “∞”). Mathematically, if we tried to calculate the NNT when AR was zero, we would be trying to calculate the reciprocal of zero.
CI in CATIE’s efficacy phase
What do NNT and CI calculations tell us about data from clinical trials such as CATIE for schizophrenia? In CATIE, 1,493 patients were randomly assigned to 1 of 5 antipsychotics—perphenazine, olanzapine, quetiapine, risperidone, or ziprasidone—for up to 18 months. Patients who received an SGA and discontinued phase 1 before 18 months could participate in phase 2:
- Those who discontinued because of poor symptom control were expected to enter the efficacy arm (2E) and receive open-label clozapine (n = 49) or an SGA not taken in phase 1 (n = 50).
- Those who discontinued phase 1 because of poor tolerability (n = 444) were expected to enter the tolerability arm (2T), and receive an SGA they had not taken in phase 1.
The investigator could choose which arm a patient entered, but many more patients entered 2T than 2E (perhaps because they were reluctant to enter a pathway in which they might receive clozapine). Those in phase 2E who were randomly assigned to clozapine knew they were receiving clozapine and that clozapine was a treatment for patients who did not have successful outcomes with other antipsychotic(s). This design may have influenced whether or not patients remained in the study.
In phase 2E, time until treatment discontinuation for any reason was statistically significantly longer for clozapine (median 10.5 months) than for quetiapine (median 3.3 months) or risperidone (median 2.8 months) but not statistically significantly longer than for olanzapine (median 2.7 months).
What is the NNT for an outcome for drug A versus drug B?
fA = frequency of outcome for drug A
fB = frequency of outcome for drug B
Attributable risk (AR) = fA-fB
NNT = 1/AR
(By convention, we round up the NNT to the next higher whole number.)
For example, let’s say drugs A and B are used to treat depression, and they result in 6-week response rates of 55% and 75%, respectively. The NNT to see a difference between drug B and drug A in terms of responders at 6 weeks can be calculated as follows:
- Difference in response rates = 0.75-0.55 = 0.20
- NNT = 1/0.20 = 5
What happens if response rates are reversed?
- Difference in response rates = 0.55–0.75 = -0.20
- NNT = 1/(–0.20) = -5
Here the NNT is –5, meaning a disadvantage for drug B, or a number needed to harm (NNH) of +5
What happens if response rates are identical?
- Difference in response rates = 0.75-0.75 = 0
- NNT = 1/0 = "infinity" (∞)
A NNT of 8 means it would take an infinite number of patients on drug A vs drug B to see a difference (in other words, no difference). This is by definition the "weakest" possible effect size.
What happens if the response rate is 100% for one intervention and zero for the other?
- Difference in response rates = 1.00–0 = 1.00
- NNT = 1/1 = 1
Theoretically, this is the "strongest" possible effect size.
Thus all possible values of NNT range from 1 to ∞, or –1 to –∞ it is not possible for a NNT to be zero.
Time to discontinuation because of inadequate therapeutic effect was significantly longer for clozapine than for olanzapine, quetiapine, or risperi-done.4 These statements give us the rank order of the tested medications’ performance and some idea of the size of the differences. We do not know, however, how often these differences will affect day-to-day patient treatment.
The question becomes “how many patients do I need to treat with clozapine instead of [olanzapine, quetiapine, or risperidone] before I see 1 extra success (defined as remaining on the medication)?” Similar questions can be asked about other outcomes, such as adverse events. NNT can convert the study results to a common language: numbers of patients.
Advantages for clozapine. NNTs for outcomes in CATIE phase 2E are shown in the Table. From the conventional analysis,4 we knew that patients randomly assigned to clozapine were more likely to stay on clozapine than patients assigned to other SGAs. The NNT comparing clozapine with quetiapine is 3, which means for every 3 patients treated with clozapine instead of quetiapine, 1 extra patient remained on the drug. A NNT of 3 is a medium to large effect size,7 similar to that seen when antidepressant treatment is compared with placebo in terms of reducing depressive symptoms by at least 50% among patients with major depressive disorder.8
The NNT comparing clozapine with risperidone was 4 and that for olanzapine was 7. The difference in all-cause discontinuation between clozapine and olanzapine was not statistically significant, however, perhaps because of a small sample size. The effectiveness analysis included
only 45 patients assigned to clozapine, 14 to quetiapine, 14 to risperidone, and 17 to olanzapine—far fewer than the 183 to 333 subjects in each arm in the phase-1 effectiveness analyses.9
Disadvantages for clozapine can be seen as “negative” NNT values in the Table. A negative NNT can be interpreted as a number needed to harm (NNH).
Tolerability. Discontinuation because of poor tolerability showed a disadvantage when clozapine was compared with risperidone, with a NNT of –9 (in other words, a NNH of 9). This means that for every 9 patients receiving clozapine instead of risperidone, 1 extra patient would discontinue because of poor tolerability.
Anticholinergic effects. Another statistically significant disadvantage is seen when clozapine was compared with olanzapine on the occurrence of urinary hesitancy, dry mouth, or constipation, with a NNT for clozapine of –5 (NNH 5). The comparison of clozapine with risperidone on this outcome, which yielded a NNT of –8, was not statistically significant. Clozapine vs quetiapine on this measure also was not statistically significant but showed an advantage for clozapine (disadvantage for quetiapine), with a NNT of 4.
Sialorrhea is a common adverse event attributed to clozapine. Here the NNTs for clozapine compared with olanzapine, risperidone, and quetiapine were –5, –5, and –4, respectively. The comparison with risperidone was not statistically significant.
Table
Using NNTs to compare clozapine’s effects in CATIE phase 2E
| Comparison | Clozapine vs olanzapine | Clozapine vs risperidone | Clozapine vs quetiapine |
|---|---|---|---|
| All cause discontinuation | 7 | 4* | 3* |
| Discontinuation because of poor efficacy | 5 | 4* | 4* |
| Discontinuation because of poor tolerability | –20 | –9* | 10 |
| Urinary hesitancy, dry mouth, constipation | –5* | –8 | 4 |
| Sialorrhea | –5* | –5 | –4* |
| *Statistically significant p<0.05 | |||
Interpreting the CI
The CI width is affected by the variability of the estimate and the sample size, not the true population effect size. This means that a larger sample size might decrease the CI width. Sometimes, narrowing the CI width will change a nonsignificant result to statistically significant. When researchers design a study, a large sample size helps minimize the chance of not finding a statistically significant difference if a true difference exists.
A CI that includes ∞ indicates a NNT that is not statistically significant, but low CI boundaries (close to 1 or –1) can suggest potentially important results and the need for more studies to provide additional data. The study might have been “under-powered” with an inadequate sample size.
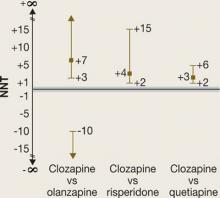
NNTs for all-cause discontinuation and their CIs when comparing clozapine with olanzapine, risperidone, or quetiapine in CATIE phase 2E are shown in Figure 1. The figure’s y-axis is centered on zero, but because a NNT must fall between 1 and ∞ (or –1 to –∞), we “grayed out” the interval around zero.
CI is easy to interpret for a statistically significant NNT. For NNT values that are not statistically significant, the CI contains 2 ranges of numbers. For the comparison of clozapine vs olanzapine, the 2 ranges are 3 to ∞ and –10 to –∞. The NNT of 7 falls within the range of 3 to ∞, but the 95% confidence interval also includes the range of –10 to –∞.
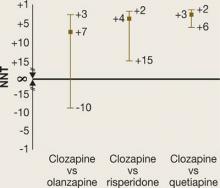
It may be easier to visualize and understand the CI by reformatting the figure so that it is centered on ∞ (Figure 2). Any CI that “crosses” ∞ represents a result that is not statistically significant. In Figure 1 and Figure 2 we also can examine the “width” of the CI. The comparison of clozapine vs quetiapine yields a NNT with a narrower CI than the comparison of clozapine vs risperidone. A narrow CI implies greater precision of our estimate of NNT and potentially its clinical importance.
Figure 1
CATIE Phase 2E: What was the advantage for clozapine?
NNTs for all-cause discontinuation and 95% confidence intervals in comparing clozapine with other SGAs. The y-axis is centered on zero, but because a NNT must fall between 1 and infinity (∞) (or –1 to –∞), the interval around zero is ‘grayed out.’
Figure 2
CATIE Phase 2E: What was the advantage for clozapine (revised)?
NNTs for all-cause discontinuation and 95% confidence intervals (CI) in comparing clozapine with other SGAs. Figure 2 shows Figure 1 reformatted to center on infinity (∞). Any CI that ‘crosses’ ∞ represents a result that is not statistically significant.Related Resources
- Confidence interval calculator. www.cebm.utoronto.ca/practise/ca/statscal.
- Guyatt G, Rennie D. Users’ guides to the medical literature: a manual for evidence-based clinical practice. Chicago, IL: AMA Press; 2001.
- Straus SE, Richardson WS, Glasziou P, et al. Evidence-based medicine: how to practice and teach EBM. 3rd ed. Edinburgh, UK: Elsevier/Churchill Livingstone; 2005.
Drug brand names
- Clozapine • Clozaril
- Olanzapine • Zyprexa
- Perphenazine • Trilafon
- Quetiapine • Seroquel
- Risperidone • Risperdal
- Ziprasidone • Geodon
Disclosures
Dr. Citrome is a consultant for, has received honoraria from, or has conducted clinical research supported by Abbott Laboratories, AstraZeneca Pharmaceuticals, Barr Laboratories, Bristol-Myers Squibb, Eli Lilly and Company, Forest Research Institute, GlaxoSmithKline, Janssen Pharmaceutica, Jazz Pharmaceuticals, and Pfizer Inc.
1. Lemonick MD. Medicine’s secret stat. Time. February 15, 2007. Available at: http://www.time.com/time/printout/0,8816,1590464,00.html. Accessed February 20, 2007.
2. Guyatt G, Cook D, Devereaux PJ, et al. Therapy. In: Guyatt G, Rennie D, eds. Users’ guides to the medical literature, chapter 1B1. Chicago, IL: AMA Press, 2002.
3. Citrome L. Dissecting clinical trials with ‘number needed to treat.’ Current Psychiatry. 2007;6(3):66-71.
4. McEvoy JP, Lieberman JA, Stroup TS, et al. Effectiveness of clozapine versus olanzapine, quetiapine, and risperidone in patients with chronic schizophrenia who did not respond to prior atypical antipsychotic treatment. Am J Psychiatry. 2006;163(4):600-10.
5. Citrome L, Stroup TS. Schizophrenia, Clinical Antipsychotic Trials of Intervention Effectiveness (CATIE), and number needed to treat: how can CATIE inform clinicians? Int J Clin Pract. 2006;60(8):933-40.
6. Altman DG. Confidence intervals for the number needed to treat. BMJ. 1998;317(7168):1309-12.
7. Kraemer HC, Kupfer DJ. Size of treatment effects and their importance to clinical research and practice. Biol Psychiatry. 2006;59(11):990-6.
8. Pinson L, Gray GE. Number needed to treat: an underused measure of treatment effect. Psychiatr Serv. 2003;54(2):145-6,154.
9. Lieberman JA, Stroup TS, McEvoy JP, et al. Clinical Antipsychotic Trials of Intervention Effectiveness (CATIE) investigators. Effectiveness of antipsychotic drugs in patients with chronic schizophrenia. N Engl J Med. 2005;353(12):1209-23.
Number needed to treat (NNT) is a measure of clinical effect that has been called medicine’s “secret stat”(Box 1).1,2 By itself, however, the NNT provides no information about whether a trial result is probably true (statistical significance). If a NNT is statistically significant, the confidence interval (CI) can tell you the range of numbers within which the truth probably lies.
In the March 2007 issue of Current Psychiatry, we described how to use NNT to interpret and apply research data in daily practice.3 In this article, we explain the “secrets” of NNT and CI by providing sample calculations and several figures for visual learning. For illustration, we analyze data from the Clinical Antipsychotic Trials of Intervention Effectiveness (CATIE) in schizophrenia, this time focusing on phase 2E—the efficacy pathway in which patients were randomly assigned to open-label clozapine or a double-blinded second-generation antipsychotic (SGA).4
Confidence intervals: Is the NNT statistically significant?
To find out a NNT’s statistical significance, you can examine the CI. A 95% CI means that the truth lies between the interval’s lower and upper bounds with a 95% probability.
Calculating CI. Although formulas to calculate the CI appear complicated,5 they are easily inserted into a Microsoft Excel-brand spreadsheet. Useful alternatives are online calculators (seeRelated Resources), which can be downloaded to your hand-held device or pocket PC.
Time magazine recently declared NNT as medicine’s “secret stat.”1 NNT allows us to place a number on how often we would see a difference between 2 interventions.
In a handbook on essentials of evidence-based clinical practice, Guyatt et al2 define NNT as “the number of patients who must receive an intervention of therapy during a specific period of time to prevent 1 adverse outcome or produce 1 positive outcome.”
If a difference in therapeutic outcome is seen once in every 5 patients treated with 1 intervention vs another (NNT of 5), it will likely influence day-to-day practice. However, if a therapeutic difference occurs in 1 of every 100 patients (NNT of 100), the difference between 2 treatments is not usually of great concern (except, for example, in assessing immunization against a rare but very dangerous illness).
A 95% CI of 5 to 15 means we are dealing with a NNT that with 95% probability falls between 5 and 15. However, if the NNT is not statistically significant, it becomes more difficult to describe the CI.6 A non-statistically significant NNT would have a CI that includes a negative number and a positive number: When comparing intervention A with intervention B, A might be better than B or B might be better than A. One bound of the CI may be a NNT of 10 and the other may be –10. It would be tempting to describe the CI as –10 to 10, but this would be misleading.
Attributable risk. NNT is calculated by taking the reciprocal of the difference between 2 rates for a particular outcome (Box 2). This difference is known as the attributable risk (AR). We can calculate a 95% CI for the AR, and the AR is considered statistically significant if both ends of the 95% CI are positive or both ends are negative.
If the 95% CI includes zero, then the AR is considered not statistically significant.
An AR value of zero means the rates of the outcome of interest are the same for the 2 interventions (there is no difference). Translating this to NNT would mean that no matter how many patients you treat with 1 intervention versus the other, you will not see a difference on the outcome of interest. The NNT would be “infinite” (represented by the symbol “∞”). Mathematically, if we tried to calculate the NNT when AR was zero, we would be trying to calculate the reciprocal of zero.
CI in CATIE’s efficacy phase
What do NNT and CI calculations tell us about data from clinical trials such as CATIE for schizophrenia? In CATIE, 1,493 patients were randomly assigned to 1 of 5 antipsychotics—perphenazine, olanzapine, quetiapine, risperidone, or ziprasidone—for up to 18 months. Patients who received an SGA and discontinued phase 1 before 18 months could participate in phase 2:
- Those who discontinued because of poor symptom control were expected to enter the efficacy arm (2E) and receive open-label clozapine (n = 49) or an SGA not taken in phase 1 (n = 50).
- Those who discontinued phase 1 because of poor tolerability (n = 444) were expected to enter the tolerability arm (2T), and receive an SGA they had not taken in phase 1.
The investigator could choose which arm a patient entered, but many more patients entered 2T than 2E (perhaps because they were reluctant to enter a pathway in which they might receive clozapine). Those in phase 2E who were randomly assigned to clozapine knew they were receiving clozapine and that clozapine was a treatment for patients who did not have successful outcomes with other antipsychotic(s). This design may have influenced whether or not patients remained in the study.
In phase 2E, time until treatment discontinuation for any reason was statistically significantly longer for clozapine (median 10.5 months) than for quetiapine (median 3.3 months) or risperidone (median 2.8 months) but not statistically significantly longer than for olanzapine (median 2.7 months).
What is the NNT for an outcome for drug A versus drug B?
fA = frequency of outcome for drug A
fB = frequency of outcome for drug B
Attributable risk (AR) = fA-fB
NNT = 1/AR
(By convention, we round up the NNT to the next higher whole number.)
For example, let’s say drugs A and B are used to treat depression, and they result in 6-week response rates of 55% and 75%, respectively. The NNT to see a difference between drug B and drug A in terms of responders at 6 weeks can be calculated as follows:
- Difference in response rates = 0.75-0.55 = 0.20
- NNT = 1/0.20 = 5
What happens if response rates are reversed?
- Difference in response rates = 0.55–0.75 = -0.20
- NNT = 1/(–0.20) = -5
Here the NNT is –5, meaning a disadvantage for drug B, or a number needed to harm (NNH) of +5
What happens if response rates are identical?
- Difference in response rates = 0.75-0.75 = 0
- NNT = 1/0 = "infinity" (∞)
A NNT of 8 means it would take an infinite number of patients on drug A vs drug B to see a difference (in other words, no difference). This is by definition the "weakest" possible effect size.
What happens if the response rate is 100% for one intervention and zero for the other?
- Difference in response rates = 1.00–0 = 1.00
- NNT = 1/1 = 1
Theoretically, this is the "strongest" possible effect size.
Thus all possible values of NNT range from 1 to ∞, or –1 to –∞ it is not possible for a NNT to be zero.
Time to discontinuation because of inadequate therapeutic effect was significantly longer for clozapine than for olanzapine, quetiapine, or risperi-done.4 These statements give us the rank order of the tested medications’ performance and some idea of the size of the differences. We do not know, however, how often these differences will affect day-to-day patient treatment.
The question becomes “how many patients do I need to treat with clozapine instead of [olanzapine, quetiapine, or risperidone] before I see 1 extra success (defined as remaining on the medication)?” Similar questions can be asked about other outcomes, such as adverse events. NNT can convert the study results to a common language: numbers of patients.
Advantages for clozapine. NNTs for outcomes in CATIE phase 2E are shown in the Table. From the conventional analysis,4 we knew that patients randomly assigned to clozapine were more likely to stay on clozapine than patients assigned to other SGAs. The NNT comparing clozapine with quetiapine is 3, which means for every 3 patients treated with clozapine instead of quetiapine, 1 extra patient remained on the drug. A NNT of 3 is a medium to large effect size,7 similar to that seen when antidepressant treatment is compared with placebo in terms of reducing depressive symptoms by at least 50% among patients with major depressive disorder.8
The NNT comparing clozapine with risperidone was 4 and that for olanzapine was 7. The difference in all-cause discontinuation between clozapine and olanzapine was not statistically significant, however, perhaps because of a small sample size. The effectiveness analysis included
only 45 patients assigned to clozapine, 14 to quetiapine, 14 to risperidone, and 17 to olanzapine—far fewer than the 183 to 333 subjects in each arm in the phase-1 effectiveness analyses.9
Disadvantages for clozapine can be seen as “negative” NNT values in the Table. A negative NNT can be interpreted as a number needed to harm (NNH).
Tolerability. Discontinuation because of poor tolerability showed a disadvantage when clozapine was compared with risperidone, with a NNT of –9 (in other words, a NNH of 9). This means that for every 9 patients receiving clozapine instead of risperidone, 1 extra patient would discontinue because of poor tolerability.
Anticholinergic effects. Another statistically significant disadvantage is seen when clozapine was compared with olanzapine on the occurrence of urinary hesitancy, dry mouth, or constipation, with a NNT for clozapine of –5 (NNH 5). The comparison of clozapine with risperidone on this outcome, which yielded a NNT of –8, was not statistically significant. Clozapine vs quetiapine on this measure also was not statistically significant but showed an advantage for clozapine (disadvantage for quetiapine), with a NNT of 4.
Sialorrhea is a common adverse event attributed to clozapine. Here the NNTs for clozapine compared with olanzapine, risperidone, and quetiapine were –5, –5, and –4, respectively. The comparison with risperidone was not statistically significant.
Table
Using NNTs to compare clozapine’s effects in CATIE phase 2E
| Comparison | Clozapine vs olanzapine | Clozapine vs risperidone | Clozapine vs quetiapine |
|---|---|---|---|
| All cause discontinuation | 7 | 4* | 3* |
| Discontinuation because of poor efficacy | 5 | 4* | 4* |
| Discontinuation because of poor tolerability | –20 | –9* | 10 |
| Urinary hesitancy, dry mouth, constipation | –5* | –8 | 4 |
| Sialorrhea | –5* | –5 | –4* |
| *Statistically significant p<0.05 | |||
Interpreting the CI
The CI width is affected by the variability of the estimate and the sample size, not the true population effect size. This means that a larger sample size might decrease the CI width. Sometimes, narrowing the CI width will change a nonsignificant result to statistically significant. When researchers design a study, a large sample size helps minimize the chance of not finding a statistically significant difference if a true difference exists.
A CI that includes ∞ indicates a NNT that is not statistically significant, but low CI boundaries (close to 1 or –1) can suggest potentially important results and the need for more studies to provide additional data. The study might have been “under-powered” with an inadequate sample size.
NNTs for all-cause discontinuation and their CIs when comparing clozapine with olanzapine, risperidone, or quetiapine in CATIE phase 2E are shown in Figure 1. The figure’s y-axis is centered on zero, but because a NNT must fall between 1 and ∞ (or –1 to –∞), we “grayed out” the interval around zero.
CI is easy to interpret for a statistically significant NNT. For NNT values that are not statistically significant, the CI contains 2 ranges of numbers. For the comparison of clozapine vs olanzapine, the 2 ranges are 3 to ∞ and –10 to –∞. The NNT of 7 falls within the range of 3 to ∞, but the 95% confidence interval also includes the range of –10 to –∞.
It may be easier to visualize and understand the CI by reformatting the figure so that it is centered on ∞ (Figure 2). Any CI that “crosses” ∞ represents a result that is not statistically significant. In Figure 1 and Figure 2 we also can examine the “width” of the CI. The comparison of clozapine vs quetiapine yields a NNT with a narrower CI than the comparison of clozapine vs risperidone. A narrow CI implies greater precision of our estimate of NNT and potentially its clinical importance.
Figure 1
CATIE Phase 2E: What was the advantage for clozapine?
NNTs for all-cause discontinuation and 95% confidence intervals in comparing clozapine with other SGAs. The y-axis is centered on zero, but because a NNT must fall between 1 and infinity (∞) (or –1 to –∞), the interval around zero is ‘grayed out.’
Figure 2
CATIE Phase 2E: What was the advantage for clozapine (revised)?
NNTs for all-cause discontinuation and 95% confidence intervals (CI) in comparing clozapine with other SGAs. Figure 2 shows Figure 1 reformatted to center on infinity (∞). Any CI that ‘crosses’ ∞ represents a result that is not statistically significant.Related Resources
- Confidence interval calculator. www.cebm.utoronto.ca/practise/ca/statscal.
- Guyatt G, Rennie D. Users’ guides to the medical literature: a manual for evidence-based clinical practice. Chicago, IL: AMA Press; 2001.
- Straus SE, Richardson WS, Glasziou P, et al. Evidence-based medicine: how to practice and teach EBM. 3rd ed. Edinburgh, UK: Elsevier/Churchill Livingstone; 2005.
Drug brand names
- Clozapine • Clozaril
- Olanzapine • Zyprexa
- Perphenazine • Trilafon
- Quetiapine • Seroquel
- Risperidone • Risperdal
- Ziprasidone • Geodon
Disclosures
Dr. Citrome is a consultant for, has received honoraria from, or has conducted clinical research supported by Abbott Laboratories, AstraZeneca Pharmaceuticals, Barr Laboratories, Bristol-Myers Squibb, Eli Lilly and Company, Forest Research Institute, GlaxoSmithKline, Janssen Pharmaceutica, Jazz Pharmaceuticals, and Pfizer Inc.
Number needed to treat (NNT) is a measure of clinical effect that has been called medicine’s “secret stat”(Box 1).1,2 By itself, however, the NNT provides no information about whether a trial result is probably true (statistical significance). If a NNT is statistically significant, the confidence interval (CI) can tell you the range of numbers within which the truth probably lies.
In the March 2007 issue of Current Psychiatry, we described how to use NNT to interpret and apply research data in daily practice.3 In this article, we explain the “secrets” of NNT and CI by providing sample calculations and several figures for visual learning. For illustration, we analyze data from the Clinical Antipsychotic Trials of Intervention Effectiveness (CATIE) in schizophrenia, this time focusing on phase 2E—the efficacy pathway in which patients were randomly assigned to open-label clozapine or a double-blinded second-generation antipsychotic (SGA).4
Confidence intervals: Is the NNT statistically significant?
To find out a NNT’s statistical significance, you can examine the CI. A 95% CI means that the truth lies between the interval’s lower and upper bounds with a 95% probability.
Calculating CI. Although formulas to calculate the CI appear complicated,5 they are easily inserted into a Microsoft Excel-brand spreadsheet. Useful alternatives are online calculators (seeRelated Resources), which can be downloaded to your hand-held device or pocket PC.
Time magazine recently declared NNT as medicine’s “secret stat.”1 NNT allows us to place a number on how often we would see a difference between 2 interventions.
In a handbook on essentials of evidence-based clinical practice, Guyatt et al2 define NNT as “the number of patients who must receive an intervention of therapy during a specific period of time to prevent 1 adverse outcome or produce 1 positive outcome.”
If a difference in therapeutic outcome is seen once in every 5 patients treated with 1 intervention vs another (NNT of 5), it will likely influence day-to-day practice. However, if a therapeutic difference occurs in 1 of every 100 patients (NNT of 100), the difference between 2 treatments is not usually of great concern (except, for example, in assessing immunization against a rare but very dangerous illness).
A 95% CI of 5 to 15 means we are dealing with a NNT that with 95% probability falls between 5 and 15. However, if the NNT is not statistically significant, it becomes more difficult to describe the CI.6 A non-statistically significant NNT would have a CI that includes a negative number and a positive number: When comparing intervention A with intervention B, A might be better than B or B might be better than A. One bound of the CI may be a NNT of 10 and the other may be –10. It would be tempting to describe the CI as –10 to 10, but this would be misleading.
Attributable risk. NNT is calculated by taking the reciprocal of the difference between 2 rates for a particular outcome (Box 2). This difference is known as the attributable risk (AR). We can calculate a 95% CI for the AR, and the AR is considered statistically significant if both ends of the 95% CI are positive or both ends are negative.
If the 95% CI includes zero, then the AR is considered not statistically significant.
An AR value of zero means the rates of the outcome of interest are the same for the 2 interventions (there is no difference). Translating this to NNT would mean that no matter how many patients you treat with 1 intervention versus the other, you will not see a difference on the outcome of interest. The NNT would be “infinite” (represented by the symbol “∞”). Mathematically, if we tried to calculate the NNT when AR was zero, we would be trying to calculate the reciprocal of zero.
CI in CATIE’s efficacy phase
What do NNT and CI calculations tell us about data from clinical trials such as CATIE for schizophrenia? In CATIE, 1,493 patients were randomly assigned to 1 of 5 antipsychotics—perphenazine, olanzapine, quetiapine, risperidone, or ziprasidone—for up to 18 months. Patients who received an SGA and discontinued phase 1 before 18 months could participate in phase 2:
- Those who discontinued because of poor symptom control were expected to enter the efficacy arm (2E) and receive open-label clozapine (n = 49) or an SGA not taken in phase 1 (n = 50).
- Those who discontinued phase 1 because of poor tolerability (n = 444) were expected to enter the tolerability arm (2T), and receive an SGA they had not taken in phase 1.
The investigator could choose which arm a patient entered, but many more patients entered 2T than 2E (perhaps because they were reluctant to enter a pathway in which they might receive clozapine). Those in phase 2E who were randomly assigned to clozapine knew they were receiving clozapine and that clozapine was a treatment for patients who did not have successful outcomes with other antipsychotic(s). This design may have influenced whether or not patients remained in the study.
In phase 2E, time until treatment discontinuation for any reason was statistically significantly longer for clozapine (median 10.5 months) than for quetiapine (median 3.3 months) or risperidone (median 2.8 months) but not statistically significantly longer than for olanzapine (median 2.7 months).
What is the NNT for an outcome for drug A versus drug B?
fA = frequency of outcome for drug A
fB = frequency of outcome for drug B
Attributable risk (AR) = fA-fB
NNT = 1/AR
(By convention, we round up the NNT to the next higher whole number.)
For example, let’s say drugs A and B are used to treat depression, and they result in 6-week response rates of 55% and 75%, respectively. The NNT to see a difference between drug B and drug A in terms of responders at 6 weeks can be calculated as follows:
- Difference in response rates = 0.75-0.55 = 0.20
- NNT = 1/0.20 = 5
What happens if response rates are reversed?
- Difference in response rates = 0.55–0.75 = -0.20
- NNT = 1/(–0.20) = -5
Here the NNT is –5, meaning a disadvantage for drug B, or a number needed to harm (NNH) of +5
What happens if response rates are identical?
- Difference in response rates = 0.75-0.75 = 0
- NNT = 1/0 = "infinity" (∞)
A NNT of 8 means it would take an infinite number of patients on drug A vs drug B to see a difference (in other words, no difference). This is by definition the "weakest" possible effect size.
What happens if the response rate is 100% for one intervention and zero for the other?
- Difference in response rates = 1.00–0 = 1.00
- NNT = 1/1 = 1
Theoretically, this is the "strongest" possible effect size.
Thus all possible values of NNT range from 1 to ∞, or –1 to –∞ it is not possible for a NNT to be zero.
Time to discontinuation because of inadequate therapeutic effect was significantly longer for clozapine than for olanzapine, quetiapine, or risperi-done.4 These statements give us the rank order of the tested medications’ performance and some idea of the size of the differences. We do not know, however, how often these differences will affect day-to-day patient treatment.
The question becomes “how many patients do I need to treat with clozapine instead of [olanzapine, quetiapine, or risperidone] before I see 1 extra success (defined as remaining on the medication)?” Similar questions can be asked about other outcomes, such as adverse events. NNT can convert the study results to a common language: numbers of patients.
Advantages for clozapine. NNTs for outcomes in CATIE phase 2E are shown in the Table. From the conventional analysis,4 we knew that patients randomly assigned to clozapine were more likely to stay on clozapine than patients assigned to other SGAs. The NNT comparing clozapine with quetiapine is 3, which means for every 3 patients treated with clozapine instead of quetiapine, 1 extra patient remained on the drug. A NNT of 3 is a medium to large effect size,7 similar to that seen when antidepressant treatment is compared with placebo in terms of reducing depressive symptoms by at least 50% among patients with major depressive disorder.8
The NNT comparing clozapine with risperidone was 4 and that for olanzapine was 7. The difference in all-cause discontinuation between clozapine and olanzapine was not statistically significant, however, perhaps because of a small sample size. The effectiveness analysis included
only 45 patients assigned to clozapine, 14 to quetiapine, 14 to risperidone, and 17 to olanzapine—far fewer than the 183 to 333 subjects in each arm in the phase-1 effectiveness analyses.9
Disadvantages for clozapine can be seen as “negative” NNT values in the Table. A negative NNT can be interpreted as a number needed to harm (NNH).
Tolerability. Discontinuation because of poor tolerability showed a disadvantage when clozapine was compared with risperidone, with a NNT of –9 (in other words, a NNH of 9). This means that for every 9 patients receiving clozapine instead of risperidone, 1 extra patient would discontinue because of poor tolerability.
Anticholinergic effects. Another statistically significant disadvantage is seen when clozapine was compared with olanzapine on the occurrence of urinary hesitancy, dry mouth, or constipation, with a NNT for clozapine of –5 (NNH 5). The comparison of clozapine with risperidone on this outcome, which yielded a NNT of –8, was not statistically significant. Clozapine vs quetiapine on this measure also was not statistically significant but showed an advantage for clozapine (disadvantage for quetiapine), with a NNT of 4.
Sialorrhea is a common adverse event attributed to clozapine. Here the NNTs for clozapine compared with olanzapine, risperidone, and quetiapine were –5, –5, and –4, respectively. The comparison with risperidone was not statistically significant.
Table
Using NNTs to compare clozapine’s effects in CATIE phase 2E
| Comparison | Clozapine vs olanzapine | Clozapine vs risperidone | Clozapine vs quetiapine |
|---|---|---|---|
| All cause discontinuation | 7 | 4* | 3* |
| Discontinuation because of poor efficacy | 5 | 4* | 4* |
| Discontinuation because of poor tolerability | –20 | –9* | 10 |
| Urinary hesitancy, dry mouth, constipation | –5* | –8 | 4 |
| Sialorrhea | –5* | –5 | –4* |
| *Statistically significant p<0.05 | |||
Interpreting the CI
The CI width is affected by the variability of the estimate and the sample size, not the true population effect size. This means that a larger sample size might decrease the CI width. Sometimes, narrowing the CI width will change a nonsignificant result to statistically significant. When researchers design a study, a large sample size helps minimize the chance of not finding a statistically significant difference if a true difference exists.
A CI that includes ∞ indicates a NNT that is not statistically significant, but low CI boundaries (close to 1 or –1) can suggest potentially important results and the need for more studies to provide additional data. The study might have been “under-powered” with an inadequate sample size.
NNTs for all-cause discontinuation and their CIs when comparing clozapine with olanzapine, risperidone, or quetiapine in CATIE phase 2E are shown in Figure 1. The figure’s y-axis is centered on zero, but because a NNT must fall between 1 and ∞ (or –1 to –∞), we “grayed out” the interval around zero.
CI is easy to interpret for a statistically significant NNT. For NNT values that are not statistically significant, the CI contains 2 ranges of numbers. For the comparison of clozapine vs olanzapine, the 2 ranges are 3 to ∞ and –10 to –∞. The NNT of 7 falls within the range of 3 to ∞, but the 95% confidence interval also includes the range of –10 to –∞.
It may be easier to visualize and understand the CI by reformatting the figure so that it is centered on ∞ (Figure 2). Any CI that “crosses” ∞ represents a result that is not statistically significant. In Figure 1 and Figure 2 we also can examine the “width” of the CI. The comparison of clozapine vs quetiapine yields a NNT with a narrower CI than the comparison of clozapine vs risperidone. A narrow CI implies greater precision of our estimate of NNT and potentially its clinical importance.
Figure 1
CATIE Phase 2E: What was the advantage for clozapine?
NNTs for all-cause discontinuation and 95% confidence intervals in comparing clozapine with other SGAs. The y-axis is centered on zero, but because a NNT must fall between 1 and infinity (∞) (or –1 to –∞), the interval around zero is ‘grayed out.’
Figure 2
CATIE Phase 2E: What was the advantage for clozapine (revised)?
NNTs for all-cause discontinuation and 95% confidence intervals (CI) in comparing clozapine with other SGAs. Figure 2 shows Figure 1 reformatted to center on infinity (∞). Any CI that ‘crosses’ ∞ represents a result that is not statistically significant.Related Resources
- Confidence interval calculator. www.cebm.utoronto.ca/practise/ca/statscal.
- Guyatt G, Rennie D. Users’ guides to the medical literature: a manual for evidence-based clinical practice. Chicago, IL: AMA Press; 2001.
- Straus SE, Richardson WS, Glasziou P, et al. Evidence-based medicine: how to practice and teach EBM. 3rd ed. Edinburgh, UK: Elsevier/Churchill Livingstone; 2005.
Drug brand names
- Clozapine • Clozaril
- Olanzapine • Zyprexa
- Perphenazine • Trilafon
- Quetiapine • Seroquel
- Risperidone • Risperdal
- Ziprasidone • Geodon
Disclosures
Dr. Citrome is a consultant for, has received honoraria from, or has conducted clinical research supported by Abbott Laboratories, AstraZeneca Pharmaceuticals, Barr Laboratories, Bristol-Myers Squibb, Eli Lilly and Company, Forest Research Institute, GlaxoSmithKline, Janssen Pharmaceutica, Jazz Pharmaceuticals, and Pfizer Inc.
1. Lemonick MD. Medicine’s secret stat. Time. February 15, 2007. Available at: http://www.time.com/time/printout/0,8816,1590464,00.html. Accessed February 20, 2007.
2. Guyatt G, Cook D, Devereaux PJ, et al. Therapy. In: Guyatt G, Rennie D, eds. Users’ guides to the medical literature, chapter 1B1. Chicago, IL: AMA Press, 2002.
3. Citrome L. Dissecting clinical trials with ‘number needed to treat.’ Current Psychiatry. 2007;6(3):66-71.
4. McEvoy JP, Lieberman JA, Stroup TS, et al. Effectiveness of clozapine versus olanzapine, quetiapine, and risperidone in patients with chronic schizophrenia who did not respond to prior atypical antipsychotic treatment. Am J Psychiatry. 2006;163(4):600-10.
5. Citrome L, Stroup TS. Schizophrenia, Clinical Antipsychotic Trials of Intervention Effectiveness (CATIE), and number needed to treat: how can CATIE inform clinicians? Int J Clin Pract. 2006;60(8):933-40.
6. Altman DG. Confidence intervals for the number needed to treat. BMJ. 1998;317(7168):1309-12.
7. Kraemer HC, Kupfer DJ. Size of treatment effects and their importance to clinical research and practice. Biol Psychiatry. 2006;59(11):990-6.
8. Pinson L, Gray GE. Number needed to treat: an underused measure of treatment effect. Psychiatr Serv. 2003;54(2):145-6,154.
9. Lieberman JA, Stroup TS, McEvoy JP, et al. Clinical Antipsychotic Trials of Intervention Effectiveness (CATIE) investigators. Effectiveness of antipsychotic drugs in patients with chronic schizophrenia. N Engl J Med. 2005;353(12):1209-23.
1. Lemonick MD. Medicine’s secret stat. Time. February 15, 2007. Available at: http://www.time.com/time/printout/0,8816,1590464,00.html. Accessed February 20, 2007.
2. Guyatt G, Cook D, Devereaux PJ, et al. Therapy. In: Guyatt G, Rennie D, eds. Users’ guides to the medical literature, chapter 1B1. Chicago, IL: AMA Press, 2002.
3. Citrome L. Dissecting clinical trials with ‘number needed to treat.’ Current Psychiatry. 2007;6(3):66-71.
4. McEvoy JP, Lieberman JA, Stroup TS, et al. Effectiveness of clozapine versus olanzapine, quetiapine, and risperidone in patients with chronic schizophrenia who did not respond to prior atypical antipsychotic treatment. Am J Psychiatry. 2006;163(4):600-10.
5. Citrome L, Stroup TS. Schizophrenia, Clinical Antipsychotic Trials of Intervention Effectiveness (CATIE), and number needed to treat: how can CATIE inform clinicians? Int J Clin Pract. 2006;60(8):933-40.
6. Altman DG. Confidence intervals for the number needed to treat. BMJ. 1998;317(7168):1309-12.
7. Kraemer HC, Kupfer DJ. Size of treatment effects and their importance to clinical research and practice. Biol Psychiatry. 2006;59(11):990-6.
8. Pinson L, Gray GE. Number needed to treat: an underused measure of treatment effect. Psychiatr Serv. 2003;54(2):145-6,154.
9. Lieberman JA, Stroup TS, McEvoy JP, et al. Clinical Antipsychotic Trials of Intervention Effectiveness (CATIE) investigators. Effectiveness of antipsychotic drugs in patients with chronic schizophrenia. N Engl J Med. 2005;353(12):1209-23.