User login
In addition to treating patients, physicians frequently have other time commitments that could include administrative, teaching, research, and family duties. Inpatient medicine is particularly unforgiving to these nonclinical duties since patients have to be assessed on a daily basis. Because of this characteristic, it is not uncommon for inpatient care responsibility to be switched between physicians to create time for nonclinical duties and personal health.
In contrast to the ambulatory setting, the influence of physician continuity of care on inpatient outcomes has not been studied frequently. Studies of inpatient continuity have primarily focused on patient discharge (likely because of its objective nature) over the weekends (likely because weekend cross-coverage is common) and have reported conflicting results.1-3 However, discontinuity of care is not isolated to the weekend since hospitalist-switches can occur at any time. In addition, expressing hospitalist continuity of care as a dichotomous variable (Was there weekend cross-coverage?) could incompletely express continuity since discharge likelihood might change with the consecutive number of days that a hospitalist is on service. This study measured the influence of hospitalist continuity throughout the patient’s hospitalization (rather than just the weekend) on daily patient discharge.
METHODS
Study Setting and Databases Used for Analysis
The study was conducted at The Ottawa Hospital, Ontario, Canada, a 1000-bed teaching hospital with 2 campuses and the primary referral center in our region. The division of general internal medicine has 6 patient services (or “teams”) at two campuses led by a staff hospitalist (exclusively general internists), a senior medical resident (2nd year of training), and various numbers of interns and medical students. Staff hospitalists do not treat more than one patient service even on the weekends.
Patients are admitted to each service on a daily basis and almost exclusively from the emergency room. Assignment of patients is essentially random since all services have the same clinical expertise. At a particular campus, the number of patients assigned daily to each service is usually equivalent between teams. Patients almost never switch between teams but may be transferred to another specialty. The study was approved by our local research ethics board.
The Patient Registry Database records for each patient the date and time of admissions (defined as the moment that a patient’s admission request is entered into the database), death or discharge from hospital (defined as the time when the patient’s discharge from hospital was entered into the database), or transfer to another specialty. It also records emergency visits, patient demographics, and location during admission. The Laboratory Database records all laboratory tests and their results.
Study Cohort
The Patient Registry Database was used to identify all individuals who were admitted to the general medicine services between January 1 and December 31, 2015. This time frame was selected to ensure that data were complete and current. General medicine services were analyzed because they are collectively the largest inpatient specialty in the hospital.
Study Outcome
The primary outcome was discharge from hospital as determined from the Patient Registry Database. Patients who died or were transferred to another service were not counted as outcomes.
Covariables
The primary exposure variable was the consecutive number of days (including weekends) that a particular hospitalist rounded on patients on a particular general medicine service. This was measured using call schedules. Other covariates included tomorrow’s expected number of discharges (TEND) daily discharge probability and its components. The TEND model4 used patient factors (age, Laboratory Abnormality Physiological Score [LAPS]5 calculated at admission) and hospitalization factors (hospital campus and service, admission urgency, day of the week, ICU status) to predict the daily discharge probability. In a validation population, these daily discharge probabilities (when summed over a particular day) strongly predicted the daily number of discharges (adjusted R2 of 89.2% [P < .001], median relative difference between observed and expected number of discharges of only 1.4% [Interquartile range,IQR: −5.5% to 7.1%]). The expected annual death risk was determined using the HOMR-now! model.6 This model used routinely collected data available at patient admission regarding the patient (sex, life-table-estimated 1-year death risk, Charlson score, current living location, previous cancer clinic status, and number of emergency department visits in the previous year) and the hospitalization (urgency, service, and LAPS score). The model explained more than half of the total variability in death likelihood of death (Nagelkirke’s R2 value of 0.53),7 was highly discriminative (C-statistic 0.92), and accurately predicted death risk (calibration slope 0.98).
Analysis
Logistic generalized estimating equation (GEE) methods were used to model the adjusted daily discharge probability.8 Data in the analytical dataset were expressed in a patient-day format (each dataset row represented one day for a particular patient). This permitted the inclusion of time-dependent covariates and allowed the GEE model to cluster hospitalization days within patients.
Model construction started with the TEND daily discharge probability and the HOMR-now! expected annual death risk (both expressed as log-odds). Then, hospitalist continuity was entered as a time-dependent covariate (ie, its value changed every day). Linear, square root, and natural logarithm forms of physician continuity were examined to determine the best fit (determined using the QIC statistic9). Finally, individual components of the TEND model were also offered to the model with those which significantly improving fit kept in the model. The GEE model used an independent correlation structure since this minimized the QIC statistic in the base model. All covariates in the final daily discharge probability model were used in the hospital death model. Analyses were conducted using SAS 9.4 (Cary, NC).
RESULTS
There were 6,405 general medicine admissions involving 5208 patients and 38,967 patient-days between January 1 and December 31, 2015 (Appendix A). Patients were elderly and were evenly divided in terms of gender, with 85% of them being admitted from the community. Comorbidities were common (median coded Charlson score was 2), with 6.0% of patients known to our cancer clinic. The median length of stay was 4 days (IQR, 2–7), with 378 admissions (5.9%) ending in death and 121 admissions (1.9%) ending in a transfer to another service.
There were 41 different staff people having at least 1 day on service. The median total service by physicians was 9 weeks (IQR 1.8–10.9 weeks). Changes in hospitalist coverage were common; hospitalizations had a median of 1 (IQR 1–2) physician switches and a median of 1 (IQR 1–2) different physicians. However, patients spent a median of 100% (IQR 66.7%–100%] of their total hospitalization with their primary hospitalist. The median duration of individual physician “stints” on service was 5 days (IQR 2–7, range 1–42).
The TEND model accurately estimated daily discharge probability for the entire cohort with 5833 and 5718.6 observed and expected discharges, respectively, during 38,967 patient-days (O/E 1.02, 95% CI 0.99–1.05). Discharge probability increased as hospitalist continuity increased, but this was statistically significant only when hospitalist continuity exceeded 4 days. Other covariables also significantly influenced discharge probability (Appendix B).
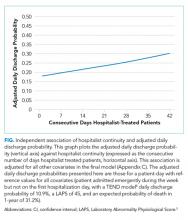
After adjusting for important covariables (Appendix C), hospitalist continuity was significantly associated with daily discharge probability (Figure). Discharge probability increased linearly with increasing consecutive days that hospitalists treated patients. For each additional consecutive day with the same hospitalist, the adjusted daily odds increased by 2% (Adj-odds ratio [OR] 1.02, 95% CI 1.01–1.02, Appendix C). When the consecutive number of days that hospitalists remained on service increased from 1 to 28 days, the adjusted discharge probability for the average patient increased from 18.1% to 25.7%, respectively. Discharge was significantly influenced by other factors (Appendix C). Continuity did not influence the risk of death in hospital (Appendix D).
DISCUSSION
In a general medicine service at a large teaching hospital, this study found that greater hospitalist continuity was associated with a significantly increased adjusted daily discharge probability, increasing (in the average patient) from 18.1% to 25.7% when the consecutive number of hospitalist days on service increased from 1 to 28 days, respectively.
The study demonstrated some interesting findings. First, it shows that shifting patient care between physicians can significantly influence patient outcomes. This could be a function of incomplete transfer of knowledge between physicians, a phenomenon that should be expected given the extensive amount of information–both explicit and implicit–that physicians collect about particular patients during their hospitalization. Second, continuity of care could increase a physician’s and a patient’s confidence in clinical decision-making. Perhaps physicians are subconsciously more trusting of their instincts (and the decisions based on those instincts) when they have been on service for a while. It is also possible that patients more readily trust recommendations of a physician they have had throughout their stay. Finally, people wishing to decrease patient length of stay might consider minimizing the extent that hospitalists sign over patient care to colleagues.
Several issues should be noted when interpreting the results of the study. First, the study examined only patient discharge and death. These are by no means the only or the most important outcomes that might be influenced by hospitalist continuity. Second, this study was limited to a single service at a single center. Third, the analysis did not account for house-staff continuity. Since hospitalist and house-staff at the study hospital invariably switched at different times, it is unlikely that hospitalist continuity was a surrogate for house-staff continuity.
Disclosures
This study was supported by the Department of Medicine, University of Ottawa, Ottawa, Ontario, Canada. The author has nothing to disclose.
1. Ali NA, Hammersley J, Hoffmann SP et al. Continuity of care in intensive care units: a cluster-randomized trial of intensivist staffing. Am J Respir Crit Care Med. 2011;184(7):803-808. PubMed
2. Epstein K, Juarez E, Epstein A, Loya K, Singer A. The impact of fragmentation of hospitalist care on length of stay. J Hosp Med. 2010;5(6):335-338. PubMed
3. Blecker S, Shine D, Park N et al. Association of weekend continuity of care with hospital length of stay. Int J Qual Health Care. 2014;26(5):530-537. PubMed
4. van Walraven C, Forster AJ. The TEND (Tomorrow’s Expected Number of Discharges) model accurately predicted the number of patients who were discharged from the hospital in the next day. J Hosp Med. In press. PubMed
5. Escobar GJ, Greene JD, Scheirer P, Gardner MN, Draper D, Kipnis P. Risk-adjusting hospital inpatient mortality using automated inpatient, outpatient, and laboratory databases. Med Care. 2008;46(3):232-239. PubMed
6. van Walraven C, Forster AJ. HOMR-now! A modification of the HOMR score that predicts 1-year death risk for hospitalized patients using data immediately available at patient admission. Am J Med. In press. PubMed
7. Nagelkerke NJ. A note on a general definition of the coefficient of determination. Biometrika. 1991;78(3):691-692.
8. Stokes ME, Davis CS, Koch GG. Generalized estimating equations. Categorical Data Analysis Using the SAS System. 2nd ed. Cary, NC: SAS Institute Inc; 2000;469-549.
9. Pan W. Akaike’s information criterion in generalized estimating equations. Biometrics. 2001;57(1):120-125. PubMed
In addition to treating patients, physicians frequently have other time commitments that could include administrative, teaching, research, and family duties. Inpatient medicine is particularly unforgiving to these nonclinical duties since patients have to be assessed on a daily basis. Because of this characteristic, it is not uncommon for inpatient care responsibility to be switched between physicians to create time for nonclinical duties and personal health.
In contrast to the ambulatory setting, the influence of physician continuity of care on inpatient outcomes has not been studied frequently. Studies of inpatient continuity have primarily focused on patient discharge (likely because of its objective nature) over the weekends (likely because weekend cross-coverage is common) and have reported conflicting results.1-3 However, discontinuity of care is not isolated to the weekend since hospitalist-switches can occur at any time. In addition, expressing hospitalist continuity of care as a dichotomous variable (Was there weekend cross-coverage?) could incompletely express continuity since discharge likelihood might change with the consecutive number of days that a hospitalist is on service. This study measured the influence of hospitalist continuity throughout the patient’s hospitalization (rather than just the weekend) on daily patient discharge.
METHODS
Study Setting and Databases Used for Analysis
The study was conducted at The Ottawa Hospital, Ontario, Canada, a 1000-bed teaching hospital with 2 campuses and the primary referral center in our region. The division of general internal medicine has 6 patient services (or “teams”) at two campuses led by a staff hospitalist (exclusively general internists), a senior medical resident (2nd year of training), and various numbers of interns and medical students. Staff hospitalists do not treat more than one patient service even on the weekends.
Patients are admitted to each service on a daily basis and almost exclusively from the emergency room. Assignment of patients is essentially random since all services have the same clinical expertise. At a particular campus, the number of patients assigned daily to each service is usually equivalent between teams. Patients almost never switch between teams but may be transferred to another specialty. The study was approved by our local research ethics board.
The Patient Registry Database records for each patient the date and time of admissions (defined as the moment that a patient’s admission request is entered into the database), death or discharge from hospital (defined as the time when the patient’s discharge from hospital was entered into the database), or transfer to another specialty. It also records emergency visits, patient demographics, and location during admission. The Laboratory Database records all laboratory tests and their results.
Study Cohort
The Patient Registry Database was used to identify all individuals who were admitted to the general medicine services between January 1 and December 31, 2015. This time frame was selected to ensure that data were complete and current. General medicine services were analyzed because they are collectively the largest inpatient specialty in the hospital.
Study Outcome
The primary outcome was discharge from hospital as determined from the Patient Registry Database. Patients who died or were transferred to another service were not counted as outcomes.
Covariables
The primary exposure variable was the consecutive number of days (including weekends) that a particular hospitalist rounded on patients on a particular general medicine service. This was measured using call schedules. Other covariates included tomorrow’s expected number of discharges (TEND) daily discharge probability and its components. The TEND model4 used patient factors (age, Laboratory Abnormality Physiological Score [LAPS]5 calculated at admission) and hospitalization factors (hospital campus and service, admission urgency, day of the week, ICU status) to predict the daily discharge probability. In a validation population, these daily discharge probabilities (when summed over a particular day) strongly predicted the daily number of discharges (adjusted R2 of 89.2% [P < .001], median relative difference between observed and expected number of discharges of only 1.4% [Interquartile range,IQR: −5.5% to 7.1%]). The expected annual death risk was determined using the HOMR-now! model.6 This model used routinely collected data available at patient admission regarding the patient (sex, life-table-estimated 1-year death risk, Charlson score, current living location, previous cancer clinic status, and number of emergency department visits in the previous year) and the hospitalization (urgency, service, and LAPS score). The model explained more than half of the total variability in death likelihood of death (Nagelkirke’s R2 value of 0.53),7 was highly discriminative (C-statistic 0.92), and accurately predicted death risk (calibration slope 0.98).
Analysis
Logistic generalized estimating equation (GEE) methods were used to model the adjusted daily discharge probability.8 Data in the analytical dataset were expressed in a patient-day format (each dataset row represented one day for a particular patient). This permitted the inclusion of time-dependent covariates and allowed the GEE model to cluster hospitalization days within patients.
Model construction started with the TEND daily discharge probability and the HOMR-now! expected annual death risk (both expressed as log-odds). Then, hospitalist continuity was entered as a time-dependent covariate (ie, its value changed every day). Linear, square root, and natural logarithm forms of physician continuity were examined to determine the best fit (determined using the QIC statistic9). Finally, individual components of the TEND model were also offered to the model with those which significantly improving fit kept in the model. The GEE model used an independent correlation structure since this minimized the QIC statistic in the base model. All covariates in the final daily discharge probability model were used in the hospital death model. Analyses were conducted using SAS 9.4 (Cary, NC).
RESULTS
There were 6,405 general medicine admissions involving 5208 patients and 38,967 patient-days between January 1 and December 31, 2015 (Appendix A). Patients were elderly and were evenly divided in terms of gender, with 85% of them being admitted from the community. Comorbidities were common (median coded Charlson score was 2), with 6.0% of patients known to our cancer clinic. The median length of stay was 4 days (IQR, 2–7), with 378 admissions (5.9%) ending in death and 121 admissions (1.9%) ending in a transfer to another service.
There were 41 different staff people having at least 1 day on service. The median total service by physicians was 9 weeks (IQR 1.8–10.9 weeks). Changes in hospitalist coverage were common; hospitalizations had a median of 1 (IQR 1–2) physician switches and a median of 1 (IQR 1–2) different physicians. However, patients spent a median of 100% (IQR 66.7%–100%] of their total hospitalization with their primary hospitalist. The median duration of individual physician “stints” on service was 5 days (IQR 2–7, range 1–42).
The TEND model accurately estimated daily discharge probability for the entire cohort with 5833 and 5718.6 observed and expected discharges, respectively, during 38,967 patient-days (O/E 1.02, 95% CI 0.99–1.05). Discharge probability increased as hospitalist continuity increased, but this was statistically significant only when hospitalist continuity exceeded 4 days. Other covariables also significantly influenced discharge probability (Appendix B).
After adjusting for important covariables (Appendix C), hospitalist continuity was significantly associated with daily discharge probability (Figure). Discharge probability increased linearly with increasing consecutive days that hospitalists treated patients. For each additional consecutive day with the same hospitalist, the adjusted daily odds increased by 2% (Adj-odds ratio [OR] 1.02, 95% CI 1.01–1.02, Appendix C). When the consecutive number of days that hospitalists remained on service increased from 1 to 28 days, the adjusted discharge probability for the average patient increased from 18.1% to 25.7%, respectively. Discharge was significantly influenced by other factors (Appendix C). Continuity did not influence the risk of death in hospital (Appendix D).
DISCUSSION
In a general medicine service at a large teaching hospital, this study found that greater hospitalist continuity was associated with a significantly increased adjusted daily discharge probability, increasing (in the average patient) from 18.1% to 25.7% when the consecutive number of hospitalist days on service increased from 1 to 28 days, respectively.
The study demonstrated some interesting findings. First, it shows that shifting patient care between physicians can significantly influence patient outcomes. This could be a function of incomplete transfer of knowledge between physicians, a phenomenon that should be expected given the extensive amount of information–both explicit and implicit–that physicians collect about particular patients during their hospitalization. Second, continuity of care could increase a physician’s and a patient’s confidence in clinical decision-making. Perhaps physicians are subconsciously more trusting of their instincts (and the decisions based on those instincts) when they have been on service for a while. It is also possible that patients more readily trust recommendations of a physician they have had throughout their stay. Finally, people wishing to decrease patient length of stay might consider minimizing the extent that hospitalists sign over patient care to colleagues.
Several issues should be noted when interpreting the results of the study. First, the study examined only patient discharge and death. These are by no means the only or the most important outcomes that might be influenced by hospitalist continuity. Second, this study was limited to a single service at a single center. Third, the analysis did not account for house-staff continuity. Since hospitalist and house-staff at the study hospital invariably switched at different times, it is unlikely that hospitalist continuity was a surrogate for house-staff continuity.
Disclosures
This study was supported by the Department of Medicine, University of Ottawa, Ottawa, Ontario, Canada. The author has nothing to disclose.
In addition to treating patients, physicians frequently have other time commitments that could include administrative, teaching, research, and family duties. Inpatient medicine is particularly unforgiving to these nonclinical duties since patients have to be assessed on a daily basis. Because of this characteristic, it is not uncommon for inpatient care responsibility to be switched between physicians to create time for nonclinical duties and personal health.
In contrast to the ambulatory setting, the influence of physician continuity of care on inpatient outcomes has not been studied frequently. Studies of inpatient continuity have primarily focused on patient discharge (likely because of its objective nature) over the weekends (likely because weekend cross-coverage is common) and have reported conflicting results.1-3 However, discontinuity of care is not isolated to the weekend since hospitalist-switches can occur at any time. In addition, expressing hospitalist continuity of care as a dichotomous variable (Was there weekend cross-coverage?) could incompletely express continuity since discharge likelihood might change with the consecutive number of days that a hospitalist is on service. This study measured the influence of hospitalist continuity throughout the patient’s hospitalization (rather than just the weekend) on daily patient discharge.
METHODS
Study Setting and Databases Used for Analysis
The study was conducted at The Ottawa Hospital, Ontario, Canada, a 1000-bed teaching hospital with 2 campuses and the primary referral center in our region. The division of general internal medicine has 6 patient services (or “teams”) at two campuses led by a staff hospitalist (exclusively general internists), a senior medical resident (2nd year of training), and various numbers of interns and medical students. Staff hospitalists do not treat more than one patient service even on the weekends.
Patients are admitted to each service on a daily basis and almost exclusively from the emergency room. Assignment of patients is essentially random since all services have the same clinical expertise. At a particular campus, the number of patients assigned daily to each service is usually equivalent between teams. Patients almost never switch between teams but may be transferred to another specialty. The study was approved by our local research ethics board.
The Patient Registry Database records for each patient the date and time of admissions (defined as the moment that a patient’s admission request is entered into the database), death or discharge from hospital (defined as the time when the patient’s discharge from hospital was entered into the database), or transfer to another specialty. It also records emergency visits, patient demographics, and location during admission. The Laboratory Database records all laboratory tests and their results.
Study Cohort
The Patient Registry Database was used to identify all individuals who were admitted to the general medicine services between January 1 and December 31, 2015. This time frame was selected to ensure that data were complete and current. General medicine services were analyzed because they are collectively the largest inpatient specialty in the hospital.
Study Outcome
The primary outcome was discharge from hospital as determined from the Patient Registry Database. Patients who died or were transferred to another service were not counted as outcomes.
Covariables
The primary exposure variable was the consecutive number of days (including weekends) that a particular hospitalist rounded on patients on a particular general medicine service. This was measured using call schedules. Other covariates included tomorrow’s expected number of discharges (TEND) daily discharge probability and its components. The TEND model4 used patient factors (age, Laboratory Abnormality Physiological Score [LAPS]5 calculated at admission) and hospitalization factors (hospital campus and service, admission urgency, day of the week, ICU status) to predict the daily discharge probability. In a validation population, these daily discharge probabilities (when summed over a particular day) strongly predicted the daily number of discharges (adjusted R2 of 89.2% [P < .001], median relative difference between observed and expected number of discharges of only 1.4% [Interquartile range,IQR: −5.5% to 7.1%]). The expected annual death risk was determined using the HOMR-now! model.6 This model used routinely collected data available at patient admission regarding the patient (sex, life-table-estimated 1-year death risk, Charlson score, current living location, previous cancer clinic status, and number of emergency department visits in the previous year) and the hospitalization (urgency, service, and LAPS score). The model explained more than half of the total variability in death likelihood of death (Nagelkirke’s R2 value of 0.53),7 was highly discriminative (C-statistic 0.92), and accurately predicted death risk (calibration slope 0.98).
Analysis
Logistic generalized estimating equation (GEE) methods were used to model the adjusted daily discharge probability.8 Data in the analytical dataset were expressed in a patient-day format (each dataset row represented one day for a particular patient). This permitted the inclusion of time-dependent covariates and allowed the GEE model to cluster hospitalization days within patients.
Model construction started with the TEND daily discharge probability and the HOMR-now! expected annual death risk (both expressed as log-odds). Then, hospitalist continuity was entered as a time-dependent covariate (ie, its value changed every day). Linear, square root, and natural logarithm forms of physician continuity were examined to determine the best fit (determined using the QIC statistic9). Finally, individual components of the TEND model were also offered to the model with those which significantly improving fit kept in the model. The GEE model used an independent correlation structure since this minimized the QIC statistic in the base model. All covariates in the final daily discharge probability model were used in the hospital death model. Analyses were conducted using SAS 9.4 (Cary, NC).
RESULTS
There were 6,405 general medicine admissions involving 5208 patients and 38,967 patient-days between January 1 and December 31, 2015 (Appendix A). Patients were elderly and were evenly divided in terms of gender, with 85% of them being admitted from the community. Comorbidities were common (median coded Charlson score was 2), with 6.0% of patients known to our cancer clinic. The median length of stay was 4 days (IQR, 2–7), with 378 admissions (5.9%) ending in death and 121 admissions (1.9%) ending in a transfer to another service.
There were 41 different staff people having at least 1 day on service. The median total service by physicians was 9 weeks (IQR 1.8–10.9 weeks). Changes in hospitalist coverage were common; hospitalizations had a median of 1 (IQR 1–2) physician switches and a median of 1 (IQR 1–2) different physicians. However, patients spent a median of 100% (IQR 66.7%–100%] of their total hospitalization with their primary hospitalist. The median duration of individual physician “stints” on service was 5 days (IQR 2–7, range 1–42).
The TEND model accurately estimated daily discharge probability for the entire cohort with 5833 and 5718.6 observed and expected discharges, respectively, during 38,967 patient-days (O/E 1.02, 95% CI 0.99–1.05). Discharge probability increased as hospitalist continuity increased, but this was statistically significant only when hospitalist continuity exceeded 4 days. Other covariables also significantly influenced discharge probability (Appendix B).
After adjusting for important covariables (Appendix C), hospitalist continuity was significantly associated with daily discharge probability (Figure). Discharge probability increased linearly with increasing consecutive days that hospitalists treated patients. For each additional consecutive day with the same hospitalist, the adjusted daily odds increased by 2% (Adj-odds ratio [OR] 1.02, 95% CI 1.01–1.02, Appendix C). When the consecutive number of days that hospitalists remained on service increased from 1 to 28 days, the adjusted discharge probability for the average patient increased from 18.1% to 25.7%, respectively. Discharge was significantly influenced by other factors (Appendix C). Continuity did not influence the risk of death in hospital (Appendix D).
DISCUSSION
In a general medicine service at a large teaching hospital, this study found that greater hospitalist continuity was associated with a significantly increased adjusted daily discharge probability, increasing (in the average patient) from 18.1% to 25.7% when the consecutive number of hospitalist days on service increased from 1 to 28 days, respectively.
The study demonstrated some interesting findings. First, it shows that shifting patient care between physicians can significantly influence patient outcomes. This could be a function of incomplete transfer of knowledge between physicians, a phenomenon that should be expected given the extensive amount of information–both explicit and implicit–that physicians collect about particular patients during their hospitalization. Second, continuity of care could increase a physician’s and a patient’s confidence in clinical decision-making. Perhaps physicians are subconsciously more trusting of their instincts (and the decisions based on those instincts) when they have been on service for a while. It is also possible that patients more readily trust recommendations of a physician they have had throughout their stay. Finally, people wishing to decrease patient length of stay might consider minimizing the extent that hospitalists sign over patient care to colleagues.
Several issues should be noted when interpreting the results of the study. First, the study examined only patient discharge and death. These are by no means the only or the most important outcomes that might be influenced by hospitalist continuity. Second, this study was limited to a single service at a single center. Third, the analysis did not account for house-staff continuity. Since hospitalist and house-staff at the study hospital invariably switched at different times, it is unlikely that hospitalist continuity was a surrogate for house-staff continuity.
Disclosures
This study was supported by the Department of Medicine, University of Ottawa, Ottawa, Ontario, Canada. The author has nothing to disclose.
1. Ali NA, Hammersley J, Hoffmann SP et al. Continuity of care in intensive care units: a cluster-randomized trial of intensivist staffing. Am J Respir Crit Care Med. 2011;184(7):803-808. PubMed
2. Epstein K, Juarez E, Epstein A, Loya K, Singer A. The impact of fragmentation of hospitalist care on length of stay. J Hosp Med. 2010;5(6):335-338. PubMed
3. Blecker S, Shine D, Park N et al. Association of weekend continuity of care with hospital length of stay. Int J Qual Health Care. 2014;26(5):530-537. PubMed
4. van Walraven C, Forster AJ. The TEND (Tomorrow’s Expected Number of Discharges) model accurately predicted the number of patients who were discharged from the hospital in the next day. J Hosp Med. In press. PubMed
5. Escobar GJ, Greene JD, Scheirer P, Gardner MN, Draper D, Kipnis P. Risk-adjusting hospital inpatient mortality using automated inpatient, outpatient, and laboratory databases. Med Care. 2008;46(3):232-239. PubMed
6. van Walraven C, Forster AJ. HOMR-now! A modification of the HOMR score that predicts 1-year death risk for hospitalized patients using data immediately available at patient admission. Am J Med. In press. PubMed
7. Nagelkerke NJ. A note on a general definition of the coefficient of determination. Biometrika. 1991;78(3):691-692.
8. Stokes ME, Davis CS, Koch GG. Generalized estimating equations. Categorical Data Analysis Using the SAS System. 2nd ed. Cary, NC: SAS Institute Inc; 2000;469-549.
9. Pan W. Akaike’s information criterion in generalized estimating equations. Biometrics. 2001;57(1):120-125. PubMed
1. Ali NA, Hammersley J, Hoffmann SP et al. Continuity of care in intensive care units: a cluster-randomized trial of intensivist staffing. Am J Respir Crit Care Med. 2011;184(7):803-808. PubMed
2. Epstein K, Juarez E, Epstein A, Loya K, Singer A. The impact of fragmentation of hospitalist care on length of stay. J Hosp Med. 2010;5(6):335-338. PubMed
3. Blecker S, Shine D, Park N et al. Association of weekend continuity of care with hospital length of stay. Int J Qual Health Care. 2014;26(5):530-537. PubMed
4. van Walraven C, Forster AJ. The TEND (Tomorrow’s Expected Number of Discharges) model accurately predicted the number of patients who were discharged from the hospital in the next day. J Hosp Med. In press. PubMed
5. Escobar GJ, Greene JD, Scheirer P, Gardner MN, Draper D, Kipnis P. Risk-adjusting hospital inpatient mortality using automated inpatient, outpatient, and laboratory databases. Med Care. 2008;46(3):232-239. PubMed
6. van Walraven C, Forster AJ. HOMR-now! A modification of the HOMR score that predicts 1-year death risk for hospitalized patients using data immediately available at patient admission. Am J Med. In press. PubMed
7. Nagelkerke NJ. A note on a general definition of the coefficient of determination. Biometrika. 1991;78(3):691-692.
8. Stokes ME, Davis CS, Koch GG. Generalized estimating equations. Categorical Data Analysis Using the SAS System. 2nd ed. Cary, NC: SAS Institute Inc; 2000;469-549.
9. Pan W. Akaike’s information criterion in generalized estimating equations. Biometrics. 2001;57(1):120-125. PubMed
© 2018 Society of Hospital Medicine