User login
The Influence of Hospitalist Continuity on the Likelihood of Patient Discharge in General Medicine Patients
In addition to treating patients, physicians frequently have other time commitments that could include administrative, teaching, research, and family duties. Inpatient medicine is particularly unforgiving to these nonclinical duties since patients have to be assessed on a daily basis. Because of this characteristic, it is not uncommon for inpatient care responsibility to be switched between physicians to create time for nonclinical duties and personal health.
In contrast to the ambulatory setting, the influence of physician continuity of care on inpatient outcomes has not been studied frequently. Studies of inpatient continuity have primarily focused on patient discharge (likely because of its objective nature) over the weekends (likely because weekend cross-coverage is common) and have reported conflicting results.1-3 However, discontinuity of care is not isolated to the weekend since hospitalist-switches can occur at any time. In addition, expressing hospitalist continuity of care as a dichotomous variable (Was there weekend cross-coverage?) could incompletely express continuity since discharge likelihood might change with the consecutive number of days that a hospitalist is on service. This study measured the influence of hospitalist continuity throughout the patient’s hospitalization (rather than just the weekend) on daily patient discharge.
METHODS
Study Setting and Databases Used for Analysis
The study was conducted at The Ottawa Hospital, Ontario, Canada, a 1000-bed teaching hospital with 2 campuses and the primary referral center in our region. The division of general internal medicine has 6 patient services (or “teams”) at two campuses led by a staff hospitalist (exclusively general internists), a senior medical resident (2nd year of training), and various numbers of interns and medical students. Staff hospitalists do not treat more than one patient service even on the weekends.
Patients are admitted to each service on a daily basis and almost exclusively from the emergency room. Assignment of patients is essentially random since all services have the same clinical expertise. At a particular campus, the number of patients assigned daily to each service is usually equivalent between teams. Patients almost never switch between teams but may be transferred to another specialty. The study was approved by our local research ethics board.
The Patient Registry Database records for each patient the date and time of admissions (defined as the moment that a patient’s admission request is entered into the database), death or discharge from hospital (defined as the time when the patient’s discharge from hospital was entered into the database), or transfer to another specialty. It also records emergency visits, patient demographics, and location during admission. The Laboratory Database records all laboratory tests and their results.
Study Cohort
The Patient Registry Database was used to identify all individuals who were admitted to the general medicine services between January 1 and December 31, 2015. This time frame was selected to ensure that data were complete and current. General medicine services were analyzed because they are collectively the largest inpatient specialty in the hospital.
Study Outcome
The primary outcome was discharge from hospital as determined from the Patient Registry Database. Patients who died or were transferred to another service were not counted as outcomes.
Covariables
The primary exposure variable was the consecutive number of days (including weekends) that a particular hospitalist rounded on patients on a particular general medicine service. This was measured using call schedules. Other covariates included tomorrow’s expected number of discharges (TEND) daily discharge probability and its components. The TEND model4 used patient factors (age, Laboratory Abnormality Physiological Score [LAPS]5 calculated at admission) and hospitalization factors (hospital campus and service, admission urgency, day of the week, ICU status) to predict the daily discharge probability. In a validation population, these daily discharge probabilities (when summed over a particular day) strongly predicted the daily number of discharges (adjusted R2 of 89.2% [P < .001], median relative difference between observed and expected number of discharges of only 1.4% [Interquartile range,IQR: −5.5% to 7.1%]). The expected annual death risk was determined using the HOMR-now! model.6 This model used routinely collected data available at patient admission regarding the patient (sex, life-table-estimated 1-year death risk, Charlson score, current living location, previous cancer clinic status, and number of emergency department visits in the previous year) and the hospitalization (urgency, service, and LAPS score). The model explained more than half of the total variability in death likelihood of death (Nagelkirke’s R2 value of 0.53),7 was highly discriminative (C-statistic 0.92), and accurately predicted death risk (calibration slope 0.98).
Analysis
Logistic generalized estimating equation (GEE) methods were used to model the adjusted daily discharge probability.8 Data in the analytical dataset were expressed in a patient-day format (each dataset row represented one day for a particular patient). This permitted the inclusion of time-dependent covariates and allowed the GEE model to cluster hospitalization days within patients.
Model construction started with the TEND daily discharge probability and the HOMR-now! expected annual death risk (both expressed as log-odds). Then, hospitalist continuity was entered as a time-dependent covariate (ie, its value changed every day). Linear, square root, and natural logarithm forms of physician continuity were examined to determine the best fit (determined using the QIC statistic9). Finally, individual components of the TEND model were also offered to the model with those which significantly improving fit kept in the model. The GEE model used an independent correlation structure since this minimized the QIC statistic in the base model. All covariates in the final daily discharge probability model were used in the hospital death model. Analyses were conducted using SAS 9.4 (Cary, NC).
RESULTS
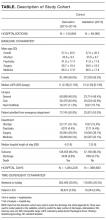
There were 6,405 general medicine admissions involving 5208 patients and 38,967 patient-days between January 1 and December 31, 2015 (Appendix A). Patients were elderly and were evenly divided in terms of gender, with 85% of them being admitted from the community. Comorbidities were common (median coded Charlson score was 2), with 6.0% of patients known to our cancer clinic. The median length of stay was 4 days (IQR, 2–7), with 378 admissions (5.9%) ending in death and 121 admissions (1.9%) ending in a transfer to another service.
There were 41 different staff people having at least 1 day on service. The median total service by physicians was 9 weeks (IQR 1.8–10.9 weeks). Changes in hospitalist coverage were common; hospitalizations had a median of 1 (IQR 1–2) physician switches and a median of 1 (IQR 1–2) different physicians. However, patients spent a median of 100% (IQR 66.7%–100%] of their total hospitalization with their primary hospitalist. The median duration of individual physician “stints” on service was 5 days (IQR 2–7, range 1–42).
The TEND model accurately estimated daily discharge probability for the entire cohort with 5833 and 5718.6 observed and expected discharges, respectively, during 38,967 patient-days (O/E 1.02, 95% CI 0.99–1.05). Discharge probability increased as hospitalist continuity increased, but this was statistically significant only when hospitalist continuity exceeded 4 days. Other covariables also significantly influenced discharge probability (Appendix B).
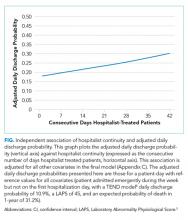
After adjusting for important covariables (Appendix C), hospitalist continuity was significantly associated with daily discharge probability (Figure). Discharge probability increased linearly with increasing consecutive days that hospitalists treated patients. For each additional consecutive day with the same hospitalist, the adjusted daily odds increased by 2% (Adj-odds ratio [OR] 1.02, 95% CI 1.01–1.02, Appendix C). When the consecutive number of days that hospitalists remained on service increased from 1 to 28 days, the adjusted discharge probability for the average patient increased from 18.1% to 25.7%, respectively. Discharge was significantly influenced by other factors (Appendix C). Continuity did not influence the risk of death in hospital (Appendix D).
DISCUSSION
In a general medicine service at a large teaching hospital, this study found that greater hospitalist continuity was associated with a significantly increased adjusted daily discharge probability, increasing (in the average patient) from 18.1% to 25.7% when the consecutive number of hospitalist days on service increased from 1 to 28 days, respectively.
The study demonstrated some interesting findings. First, it shows that shifting patient care between physicians can significantly influence patient outcomes. This could be a function of incomplete transfer of knowledge between physicians, a phenomenon that should be expected given the extensive amount of information–both explicit and implicit–that physicians collect about particular patients during their hospitalization. Second, continuity of care could increase a physician’s and a patient’s confidence in clinical decision-making. Perhaps physicians are subconsciously more trusting of their instincts (and the decisions based on those instincts) when they have been on service for a while. It is also possible that patients more readily trust recommendations of a physician they have had throughout their stay. Finally, people wishing to decrease patient length of stay might consider minimizing the extent that hospitalists sign over patient care to colleagues.
Several issues should be noted when interpreting the results of the study. First, the study examined only patient discharge and death. These are by no means the only or the most important outcomes that might be influenced by hospitalist continuity. Second, this study was limited to a single service at a single center. Third, the analysis did not account for house-staff continuity. Since hospitalist and house-staff at the study hospital invariably switched at different times, it is unlikely that hospitalist continuity was a surrogate for house-staff continuity.
Disclosures
This study was supported by the Department of Medicine, University of Ottawa, Ottawa, Ontario, Canada. The author has nothing to disclose.
1. Ali NA, Hammersley J, Hoffmann SP et al. Continuity of care in intensive care units: a cluster-randomized trial of intensivist staffing. Am J Respir Crit Care Med. 2011;184(7):803-808. PubMed
2. Epstein K, Juarez E, Epstein A, Loya K, Singer A. The impact of fragmentation of hospitalist care on length of stay. J Hosp Med. 2010;5(6):335-338. PubMed
3. Blecker S, Shine D, Park N et al. Association of weekend continuity of care with hospital length of stay. Int J Qual Health Care. 2014;26(5):530-537. PubMed
4. van Walraven C, Forster AJ. The TEND (Tomorrow’s Expected Number of Discharges) model accurately predicted the number of patients who were discharged from the hospital in the next day. J Hosp Med. In press. PubMed
5. Escobar GJ, Greene JD, Scheirer P, Gardner MN, Draper D, Kipnis P. Risk-adjusting hospital inpatient mortality using automated inpatient, outpatient, and laboratory databases. Med Care. 2008;46(3):232-239. PubMed
6. van Walraven C, Forster AJ. HOMR-now! A modification of the HOMR score that predicts 1-year death risk for hospitalized patients using data immediately available at patient admission. Am J Med. In press. PubMed
7. Nagelkerke NJ. A note on a general definition of the coefficient of determination. Biometrika. 1991;78(3):691-692.
8. Stokes ME, Davis CS, Koch GG. Generalized estimating equations. Categorical Data Analysis Using the SAS System. 2nd ed. Cary, NC: SAS Institute Inc; 2000;469-549.
9. Pan W. Akaike’s information criterion in generalized estimating equations. Biometrics. 2001;57(1):120-125. PubMed
In addition to treating patients, physicians frequently have other time commitments that could include administrative, teaching, research, and family duties. Inpatient medicine is particularly unforgiving to these nonclinical duties since patients have to be assessed on a daily basis. Because of this characteristic, it is not uncommon for inpatient care responsibility to be switched between physicians to create time for nonclinical duties and personal health.
In contrast to the ambulatory setting, the influence of physician continuity of care on inpatient outcomes has not been studied frequently. Studies of inpatient continuity have primarily focused on patient discharge (likely because of its objective nature) over the weekends (likely because weekend cross-coverage is common) and have reported conflicting results.1-3 However, discontinuity of care is not isolated to the weekend since hospitalist-switches can occur at any time. In addition, expressing hospitalist continuity of care as a dichotomous variable (Was there weekend cross-coverage?) could incompletely express continuity since discharge likelihood might change with the consecutive number of days that a hospitalist is on service. This study measured the influence of hospitalist continuity throughout the patient’s hospitalization (rather than just the weekend) on daily patient discharge.
METHODS
Study Setting and Databases Used for Analysis
The study was conducted at The Ottawa Hospital, Ontario, Canada, a 1000-bed teaching hospital with 2 campuses and the primary referral center in our region. The division of general internal medicine has 6 patient services (or “teams”) at two campuses led by a staff hospitalist (exclusively general internists), a senior medical resident (2nd year of training), and various numbers of interns and medical students. Staff hospitalists do not treat more than one patient service even on the weekends.
Patients are admitted to each service on a daily basis and almost exclusively from the emergency room. Assignment of patients is essentially random since all services have the same clinical expertise. At a particular campus, the number of patients assigned daily to each service is usually equivalent between teams. Patients almost never switch between teams but may be transferred to another specialty. The study was approved by our local research ethics board.
The Patient Registry Database records for each patient the date and time of admissions (defined as the moment that a patient’s admission request is entered into the database), death or discharge from hospital (defined as the time when the patient’s discharge from hospital was entered into the database), or transfer to another specialty. It also records emergency visits, patient demographics, and location during admission. The Laboratory Database records all laboratory tests and their results.
Study Cohort
The Patient Registry Database was used to identify all individuals who were admitted to the general medicine services between January 1 and December 31, 2015. This time frame was selected to ensure that data were complete and current. General medicine services were analyzed because they are collectively the largest inpatient specialty in the hospital.
Study Outcome
The primary outcome was discharge from hospital as determined from the Patient Registry Database. Patients who died or were transferred to another service were not counted as outcomes.
Covariables
The primary exposure variable was the consecutive number of days (including weekends) that a particular hospitalist rounded on patients on a particular general medicine service. This was measured using call schedules. Other covariates included tomorrow’s expected number of discharges (TEND) daily discharge probability and its components. The TEND model4 used patient factors (age, Laboratory Abnormality Physiological Score [LAPS]5 calculated at admission) and hospitalization factors (hospital campus and service, admission urgency, day of the week, ICU status) to predict the daily discharge probability. In a validation population, these daily discharge probabilities (when summed over a particular day) strongly predicted the daily number of discharges (adjusted R2 of 89.2% [P < .001], median relative difference between observed and expected number of discharges of only 1.4% [Interquartile range,IQR: −5.5% to 7.1%]). The expected annual death risk was determined using the HOMR-now! model.6 This model used routinely collected data available at patient admission regarding the patient (sex, life-table-estimated 1-year death risk, Charlson score, current living location, previous cancer clinic status, and number of emergency department visits in the previous year) and the hospitalization (urgency, service, and LAPS score). The model explained more than half of the total variability in death likelihood of death (Nagelkirke’s R2 value of 0.53),7 was highly discriminative (C-statistic 0.92), and accurately predicted death risk (calibration slope 0.98).
Analysis
Logistic generalized estimating equation (GEE) methods were used to model the adjusted daily discharge probability.8 Data in the analytical dataset were expressed in a patient-day format (each dataset row represented one day for a particular patient). This permitted the inclusion of time-dependent covariates and allowed the GEE model to cluster hospitalization days within patients.
Model construction started with the TEND daily discharge probability and the HOMR-now! expected annual death risk (both expressed as log-odds). Then, hospitalist continuity was entered as a time-dependent covariate (ie, its value changed every day). Linear, square root, and natural logarithm forms of physician continuity were examined to determine the best fit (determined using the QIC statistic9). Finally, individual components of the TEND model were also offered to the model with those which significantly improving fit kept in the model. The GEE model used an independent correlation structure since this minimized the QIC statistic in the base model. All covariates in the final daily discharge probability model were used in the hospital death model. Analyses were conducted using SAS 9.4 (Cary, NC).
RESULTS
There were 6,405 general medicine admissions involving 5208 patients and 38,967 patient-days between January 1 and December 31, 2015 (Appendix A). Patients were elderly and were evenly divided in terms of gender, with 85% of them being admitted from the community. Comorbidities were common (median coded Charlson score was 2), with 6.0% of patients known to our cancer clinic. The median length of stay was 4 days (IQR, 2–7), with 378 admissions (5.9%) ending in death and 121 admissions (1.9%) ending in a transfer to another service.
There were 41 different staff people having at least 1 day on service. The median total service by physicians was 9 weeks (IQR 1.8–10.9 weeks). Changes in hospitalist coverage were common; hospitalizations had a median of 1 (IQR 1–2) physician switches and a median of 1 (IQR 1–2) different physicians. However, patients spent a median of 100% (IQR 66.7%–100%] of their total hospitalization with their primary hospitalist. The median duration of individual physician “stints” on service was 5 days (IQR 2–7, range 1–42).
The TEND model accurately estimated daily discharge probability for the entire cohort with 5833 and 5718.6 observed and expected discharges, respectively, during 38,967 patient-days (O/E 1.02, 95% CI 0.99–1.05). Discharge probability increased as hospitalist continuity increased, but this was statistically significant only when hospitalist continuity exceeded 4 days. Other covariables also significantly influenced discharge probability (Appendix B).
After adjusting for important covariables (Appendix C), hospitalist continuity was significantly associated with daily discharge probability (Figure). Discharge probability increased linearly with increasing consecutive days that hospitalists treated patients. For each additional consecutive day with the same hospitalist, the adjusted daily odds increased by 2% (Adj-odds ratio [OR] 1.02, 95% CI 1.01–1.02, Appendix C). When the consecutive number of days that hospitalists remained on service increased from 1 to 28 days, the adjusted discharge probability for the average patient increased from 18.1% to 25.7%, respectively. Discharge was significantly influenced by other factors (Appendix C). Continuity did not influence the risk of death in hospital (Appendix D).
DISCUSSION
In a general medicine service at a large teaching hospital, this study found that greater hospitalist continuity was associated with a significantly increased adjusted daily discharge probability, increasing (in the average patient) from 18.1% to 25.7% when the consecutive number of hospitalist days on service increased from 1 to 28 days, respectively.
The study demonstrated some interesting findings. First, it shows that shifting patient care between physicians can significantly influence patient outcomes. This could be a function of incomplete transfer of knowledge between physicians, a phenomenon that should be expected given the extensive amount of information–both explicit and implicit–that physicians collect about particular patients during their hospitalization. Second, continuity of care could increase a physician’s and a patient’s confidence in clinical decision-making. Perhaps physicians are subconsciously more trusting of their instincts (and the decisions based on those instincts) when they have been on service for a while. It is also possible that patients more readily trust recommendations of a physician they have had throughout their stay. Finally, people wishing to decrease patient length of stay might consider minimizing the extent that hospitalists sign over patient care to colleagues.
Several issues should be noted when interpreting the results of the study. First, the study examined only patient discharge and death. These are by no means the only or the most important outcomes that might be influenced by hospitalist continuity. Second, this study was limited to a single service at a single center. Third, the analysis did not account for house-staff continuity. Since hospitalist and house-staff at the study hospital invariably switched at different times, it is unlikely that hospitalist continuity was a surrogate for house-staff continuity.
Disclosures
This study was supported by the Department of Medicine, University of Ottawa, Ottawa, Ontario, Canada. The author has nothing to disclose.
In addition to treating patients, physicians frequently have other time commitments that could include administrative, teaching, research, and family duties. Inpatient medicine is particularly unforgiving to these nonclinical duties since patients have to be assessed on a daily basis. Because of this characteristic, it is not uncommon for inpatient care responsibility to be switched between physicians to create time for nonclinical duties and personal health.
In contrast to the ambulatory setting, the influence of physician continuity of care on inpatient outcomes has not been studied frequently. Studies of inpatient continuity have primarily focused on patient discharge (likely because of its objective nature) over the weekends (likely because weekend cross-coverage is common) and have reported conflicting results.1-3 However, discontinuity of care is not isolated to the weekend since hospitalist-switches can occur at any time. In addition, expressing hospitalist continuity of care as a dichotomous variable (Was there weekend cross-coverage?) could incompletely express continuity since discharge likelihood might change with the consecutive number of days that a hospitalist is on service. This study measured the influence of hospitalist continuity throughout the patient’s hospitalization (rather than just the weekend) on daily patient discharge.
METHODS
Study Setting and Databases Used for Analysis
The study was conducted at The Ottawa Hospital, Ontario, Canada, a 1000-bed teaching hospital with 2 campuses and the primary referral center in our region. The division of general internal medicine has 6 patient services (or “teams”) at two campuses led by a staff hospitalist (exclusively general internists), a senior medical resident (2nd year of training), and various numbers of interns and medical students. Staff hospitalists do not treat more than one patient service even on the weekends.
Patients are admitted to each service on a daily basis and almost exclusively from the emergency room. Assignment of patients is essentially random since all services have the same clinical expertise. At a particular campus, the number of patients assigned daily to each service is usually equivalent between teams. Patients almost never switch between teams but may be transferred to another specialty. The study was approved by our local research ethics board.
The Patient Registry Database records for each patient the date and time of admissions (defined as the moment that a patient’s admission request is entered into the database), death or discharge from hospital (defined as the time when the patient’s discharge from hospital was entered into the database), or transfer to another specialty. It also records emergency visits, patient demographics, and location during admission. The Laboratory Database records all laboratory tests and their results.
Study Cohort
The Patient Registry Database was used to identify all individuals who were admitted to the general medicine services between January 1 and December 31, 2015. This time frame was selected to ensure that data were complete and current. General medicine services were analyzed because they are collectively the largest inpatient specialty in the hospital.
Study Outcome
The primary outcome was discharge from hospital as determined from the Patient Registry Database. Patients who died or were transferred to another service were not counted as outcomes.
Covariables
The primary exposure variable was the consecutive number of days (including weekends) that a particular hospitalist rounded on patients on a particular general medicine service. This was measured using call schedules. Other covariates included tomorrow’s expected number of discharges (TEND) daily discharge probability and its components. The TEND model4 used patient factors (age, Laboratory Abnormality Physiological Score [LAPS]5 calculated at admission) and hospitalization factors (hospital campus and service, admission urgency, day of the week, ICU status) to predict the daily discharge probability. In a validation population, these daily discharge probabilities (when summed over a particular day) strongly predicted the daily number of discharges (adjusted R2 of 89.2% [P < .001], median relative difference between observed and expected number of discharges of only 1.4% [Interquartile range,IQR: −5.5% to 7.1%]). The expected annual death risk was determined using the HOMR-now! model.6 This model used routinely collected data available at patient admission regarding the patient (sex, life-table-estimated 1-year death risk, Charlson score, current living location, previous cancer clinic status, and number of emergency department visits in the previous year) and the hospitalization (urgency, service, and LAPS score). The model explained more than half of the total variability in death likelihood of death (Nagelkirke’s R2 value of 0.53),7 was highly discriminative (C-statistic 0.92), and accurately predicted death risk (calibration slope 0.98).
Analysis
Logistic generalized estimating equation (GEE) methods were used to model the adjusted daily discharge probability.8 Data in the analytical dataset were expressed in a patient-day format (each dataset row represented one day for a particular patient). This permitted the inclusion of time-dependent covariates and allowed the GEE model to cluster hospitalization days within patients.
Model construction started with the TEND daily discharge probability and the HOMR-now! expected annual death risk (both expressed as log-odds). Then, hospitalist continuity was entered as a time-dependent covariate (ie, its value changed every day). Linear, square root, and natural logarithm forms of physician continuity were examined to determine the best fit (determined using the QIC statistic9). Finally, individual components of the TEND model were also offered to the model with those which significantly improving fit kept in the model. The GEE model used an independent correlation structure since this minimized the QIC statistic in the base model. All covariates in the final daily discharge probability model were used in the hospital death model. Analyses were conducted using SAS 9.4 (Cary, NC).
RESULTS
There were 6,405 general medicine admissions involving 5208 patients and 38,967 patient-days between January 1 and December 31, 2015 (Appendix A). Patients were elderly and were evenly divided in terms of gender, with 85% of them being admitted from the community. Comorbidities were common (median coded Charlson score was 2), with 6.0% of patients known to our cancer clinic. The median length of stay was 4 days (IQR, 2–7), with 378 admissions (5.9%) ending in death and 121 admissions (1.9%) ending in a transfer to another service.
There were 41 different staff people having at least 1 day on service. The median total service by physicians was 9 weeks (IQR 1.8–10.9 weeks). Changes in hospitalist coverage were common; hospitalizations had a median of 1 (IQR 1–2) physician switches and a median of 1 (IQR 1–2) different physicians. However, patients spent a median of 100% (IQR 66.7%–100%] of their total hospitalization with their primary hospitalist. The median duration of individual physician “stints” on service was 5 days (IQR 2–7, range 1–42).
The TEND model accurately estimated daily discharge probability for the entire cohort with 5833 and 5718.6 observed and expected discharges, respectively, during 38,967 patient-days (O/E 1.02, 95% CI 0.99–1.05). Discharge probability increased as hospitalist continuity increased, but this was statistically significant only when hospitalist continuity exceeded 4 days. Other covariables also significantly influenced discharge probability (Appendix B).
After adjusting for important covariables (Appendix C), hospitalist continuity was significantly associated with daily discharge probability (Figure). Discharge probability increased linearly with increasing consecutive days that hospitalists treated patients. For each additional consecutive day with the same hospitalist, the adjusted daily odds increased by 2% (Adj-odds ratio [OR] 1.02, 95% CI 1.01–1.02, Appendix C). When the consecutive number of days that hospitalists remained on service increased from 1 to 28 days, the adjusted discharge probability for the average patient increased from 18.1% to 25.7%, respectively. Discharge was significantly influenced by other factors (Appendix C). Continuity did not influence the risk of death in hospital (Appendix D).
DISCUSSION
In a general medicine service at a large teaching hospital, this study found that greater hospitalist continuity was associated with a significantly increased adjusted daily discharge probability, increasing (in the average patient) from 18.1% to 25.7% when the consecutive number of hospitalist days on service increased from 1 to 28 days, respectively.
The study demonstrated some interesting findings. First, it shows that shifting patient care between physicians can significantly influence patient outcomes. This could be a function of incomplete transfer of knowledge between physicians, a phenomenon that should be expected given the extensive amount of information–both explicit and implicit–that physicians collect about particular patients during their hospitalization. Second, continuity of care could increase a physician’s and a patient’s confidence in clinical decision-making. Perhaps physicians are subconsciously more trusting of their instincts (and the decisions based on those instincts) when they have been on service for a while. It is also possible that patients more readily trust recommendations of a physician they have had throughout their stay. Finally, people wishing to decrease patient length of stay might consider minimizing the extent that hospitalists sign over patient care to colleagues.
Several issues should be noted when interpreting the results of the study. First, the study examined only patient discharge and death. These are by no means the only or the most important outcomes that might be influenced by hospitalist continuity. Second, this study was limited to a single service at a single center. Third, the analysis did not account for house-staff continuity. Since hospitalist and house-staff at the study hospital invariably switched at different times, it is unlikely that hospitalist continuity was a surrogate for house-staff continuity.
Disclosures
This study was supported by the Department of Medicine, University of Ottawa, Ottawa, Ontario, Canada. The author has nothing to disclose.
1. Ali NA, Hammersley J, Hoffmann SP et al. Continuity of care in intensive care units: a cluster-randomized trial of intensivist staffing. Am J Respir Crit Care Med. 2011;184(7):803-808. PubMed
2. Epstein K, Juarez E, Epstein A, Loya K, Singer A. The impact of fragmentation of hospitalist care on length of stay. J Hosp Med. 2010;5(6):335-338. PubMed
3. Blecker S, Shine D, Park N et al. Association of weekend continuity of care with hospital length of stay. Int J Qual Health Care. 2014;26(5):530-537. PubMed
4. van Walraven C, Forster AJ. The TEND (Tomorrow’s Expected Number of Discharges) model accurately predicted the number of patients who were discharged from the hospital in the next day. J Hosp Med. In press. PubMed
5. Escobar GJ, Greene JD, Scheirer P, Gardner MN, Draper D, Kipnis P. Risk-adjusting hospital inpatient mortality using automated inpatient, outpatient, and laboratory databases. Med Care. 2008;46(3):232-239. PubMed
6. van Walraven C, Forster AJ. HOMR-now! A modification of the HOMR score that predicts 1-year death risk for hospitalized patients using data immediately available at patient admission. Am J Med. In press. PubMed
7. Nagelkerke NJ. A note on a general definition of the coefficient of determination. Biometrika. 1991;78(3):691-692.
8. Stokes ME, Davis CS, Koch GG. Generalized estimating equations. Categorical Data Analysis Using the SAS System. 2nd ed. Cary, NC: SAS Institute Inc; 2000;469-549.
9. Pan W. Akaike’s information criterion in generalized estimating equations. Biometrics. 2001;57(1):120-125. PubMed
1. Ali NA, Hammersley J, Hoffmann SP et al. Continuity of care in intensive care units: a cluster-randomized trial of intensivist staffing. Am J Respir Crit Care Med. 2011;184(7):803-808. PubMed
2. Epstein K, Juarez E, Epstein A, Loya K, Singer A. The impact of fragmentation of hospitalist care on length of stay. J Hosp Med. 2010;5(6):335-338. PubMed
3. Blecker S, Shine D, Park N et al. Association of weekend continuity of care with hospital length of stay. Int J Qual Health Care. 2014;26(5):530-537. PubMed
4. van Walraven C, Forster AJ. The TEND (Tomorrow’s Expected Number of Discharges) model accurately predicted the number of patients who were discharged from the hospital in the next day. J Hosp Med. In press. PubMed
5. Escobar GJ, Greene JD, Scheirer P, Gardner MN, Draper D, Kipnis P. Risk-adjusting hospital inpatient mortality using automated inpatient, outpatient, and laboratory databases. Med Care. 2008;46(3):232-239. PubMed
6. van Walraven C, Forster AJ. HOMR-now! A modification of the HOMR score that predicts 1-year death risk for hospitalized patients using data immediately available at patient admission. Am J Med. In press. PubMed
7. Nagelkerke NJ. A note on a general definition of the coefficient of determination. Biometrika. 1991;78(3):691-692.
8. Stokes ME, Davis CS, Koch GG. Generalized estimating equations. Categorical Data Analysis Using the SAS System. 2nd ed. Cary, NC: SAS Institute Inc; 2000;469-549.
9. Pan W. Akaike’s information criterion in generalized estimating equations. Biometrics. 2001;57(1):120-125. PubMed
© 2018 Society of Hospital Medicine
The TEND (Tomorrow’s Expected Number of Discharges) Model Accurately Predicted the Number of Patients Who Were Discharged from the Hospital the Next Day
Hospitals typically allocate beds based on historical patient volumes. If funding decreases, hospitals will usually try to maximize resource utilization by allocating beds to attain occupancies close to 100% for significant periods of time. This will invariably cause days in which hospital occupancy exceeds capacity, at which time critical entry points (such as the emergency department and operating room) will become blocked. This creates significant concerns over the patient quality of care.
Hospital administrators have very few options when hospital occupancy exceeds 100%. They could postpone admissions for “planned” cases, bring in additional staff to increase capacity, or instigate additional methods to increase hospital discharges such as expanding care resources in the community. All options are costly, bothersome, or cannot be actioned immediately. The need for these options could be minimized by enabling hospital administrators to make more informed decisions regarding hospital bed management by knowing the likely number of discharges in the next 24 hours.
Predicting the number of people who will be discharged in the next day can be approached in several ways. One approach would be to calculate each patient’s expected length of stay and then use the variation around that estimate to calculate each day’s discharge probability. Several studies have attempted to model hospital length of stay using a broad assortment of methodologies, but a mechanism to accurately predict this outcome has been elusive1,2 (with Verburg et al.3 concluding in their study’s abstract that “…it is difficult to predict length of stay…”). A second approach would be to use survival analysis methods to generate each patient’s hazard of discharge over time, which could be directly converted to an expected daily risk of discharge. However, this approach is complicated by the concurrent need to include time-dependent covariates and consider the competing risk of death in hospital, which can complicate survival modeling.4,5 A third approach would be the implementation of a longitudinal analysis using marginal models to predict the daily probability of discharge,6 but this method quickly overwhelms computer resources when large datasets are present.
In this study, we decided to use nonparametric models to predict the daily number of hospital discharges. We first identified patient groups with distinct discharge patterns. We then calculated the conditional daily discharge probability of patients in each of these groups. Finally, these conditional daily discharge probabilities were then summed for each hospital day to generate the expected number of discharges in the next 24 hours. This paper details the methods we used to create our model and the accuracy of its predictions.
METHODS
Study Setting and Databases Used for Analysis
The study took place at The Ottawa Hospital, a 1000-bed teaching hospital with 3 campuses that is the primary referral center in our region. The study was approved by our local research ethics board.
The Patient Registry Database records the date and time of admission for each patient (defined as the moment that a patient’s admission request is registered in the patient registration) and discharge (defined as the time when the patient’s discharge from hospital was entered into the patient registration) for hospital encounters. Emergency department encounters were also identified in the Patient Registry Database along with admission service, patient age and sex, and patient location throughout the admission. The Laboratory Database records all laboratory studies and results on all patients at the hospital.
Study Cohort
We used the Patient Registry Database to identify all people aged 1 year or more who were admitted to the hospital between January 1, 2013, and December 31, 2015. This time frame was selected to (i) ensure that data were complete; and (ii) complete calendar years of data were available for both derivation (patient-days in 2013-2014) and validation (2015) cohorts. Patients who were observed in the emergency room without admission to hospital were not included.
Study Outcome
The study outcome was the number of patients discharged from the hospital each day. For the analysis, the reference point for each day was 1 second past midnight; therefore, values for time-dependent covariates up to and including midnight were used to predict the number of discharges in the next 24 hours.
Study Covariates
Baseline (ie, time-independent) covariates included patient age and sex, admission service, hospital campus, whether or not the patient was admitted from the emergency department (all determined from the Patient Registry Database), and the Laboratory-based Acute Physiological Score (LAPS). The latter, which was calculated with the Laboratory Database using results for 14 tests (arterial pH, PaCO2, PaO2, anion gap, hematocrit, total white blood cell count, serum albumin, total bilirubin, creatinine, urea nitrogen, glucose, sodium, bicarbonate, and troponin I) measured in the 24-hour time frame preceding hospitalization, was derived by Escobar and colleagues7 to measure severity of illness and was subsequently validated in our hospital.8 The independent association of each laboratory perturbation with risk of death in hospital is reflected by the number of points assigned to each lab value with the total LAPS being the sum of these values. Time-dependent covariates included weekday in hospital and whether or not patients were in the intensive care unit.
Analysis
We used 3 stages to create a model to predict the daily expected number of discharges: we identified discharge risk strata containing patients having similar discharge patterns using data from patients in the derivation cohort (first stage); then, we generated the preliminary probability of discharge by determining the daily discharge probability in each discharge risk strata (second stage); finally, we modified the probability from the second stage based on the weekday and admission service and summed these probabilities to create the expected number of discharges on a particular date (third stage).
The first stage identified discharge risk strata based on the covariates listed above. This was determined by using a survival tree approach9 with proportional hazard regression models to generate the “splits.” These models were offered all covariates listed in the Study Covariates section. Admission service was clustered within 4 departments (obstetrics/gynecology, psychiatry, surgery, and medicine) and day of week was “binarized” into weekday/weekend-holiday (because the use of categorical variables with large numbers of groups can “stunt” regression trees due to small numbers of patients—and, therefore, statistical power—in each subgroup). The proportional hazards model identified the covariate having the strongest association with time to discharge (based on the Wald X2 value divided by the degrees of freedom). This variable was then used to split the cohort into subgroups (with continuous covariates being categorized into quartiles). The proportional hazards model was then repeated in each subgroup (with the previous splitting variable[s] excluded from the model). This process continued until no variable was associated with time to discharge with a P value less than .0001. This survival-tree was then used to cluster all patients into distinct discharge risk strata.
In the second stage, we generated the preliminary probability of discharge for a specific date. This was calculated by assigning all patients in hospital to their discharge risk strata (Appendix). We then measured the probability of discharge on each hospitalization day in all discharge risk strata using data from the previous 180 days (we only used the prior 180 days of data to account for temporal changes in hospital discharge patterns). For example, consider a 75-year-old patient on her third hospital day under obstetrics/gynecology on December 19, 2015 (a Saturday). This patient would be assigned to risk stratum #133 (Appendix A). We then measured the probability of discharge of all patients in this discharge risk stratum hospitalized in the previous 6 months (ie, between June 22, 2015, and December 18, 2015) on each hospital day. For risk stratum #133, the probability of discharge on hospital day 3 was 0.1111; therefore, our sample patient’s preliminary expected discharge probability was 0.1111.
To attain stable daily discharge probability estimates, a minimum of 50 patients per discharge risk stratum-hospitalization day combination was required. If there were less than 50 patients for a particular hospitalization day in a particular discharge risk stratum, we grouped hospitalization days in that risk stratum together until the minimum of 50 patients was collected.
The third (and final) stage accounted for the lack of granularity when we created the discharge risk strata in the first stage. As we mentioned above, admission service was clustered into 4 departments and the day of week was clustered into weekend/weekday. However, important variations in discharge probabilities could still exist within departments and between particular days of the week.10 Therefore, we created a correction factor to adjust the preliminary expected number of discharges based on the admission division and day of week. This correction factor used data from the 180 days prior to the analysis date within which the expected daily number of discharges was calculated (using the methods above). The correction factor was the relative difference between the observed and expected number of discharges within each division-day of week grouping.
For example, to calculate the correction factor for our sample patient presented above (75-year-old patient on hospital day 3 under gynecology on Saturday, December 19, 2015), we measured the observed number of discharges from gynecology on Saturdays between June 22, 2015, and December 18, 2015, (n = 206) and the expected number of discharges (n = 195.255) resulting in a correction factor of (observed-expected)/expected = (195.255-206)/195.206 = 0.05503. Therefore, the final expected discharge probability for our sample patient was 0.1111+0.1111*0.05503=0.1172. The expected number of discharges on a particular date was the preliminary expected number of discharges on that date (generated in the second stage) multiplied by the correction factor for the corresponding division-day or week group.
RESULTS
There were 192,859 admissions involving patients more than 1 year of age that spent at least part of their hospitalization between January 1, 2013, and December 31, 2015 (Table). Patients were middle-aged and slightly female predominant, with about half being admitted from the emergency department. Approximately 80% of admissions were to surgical or medical services. More than 95% of admissions ended with a discharge from the hospital with the remainder ending in a death. Almost 30% of hospitalization days occurred on weekends or holidays. Hospitalizations in the derivation (2013-2014) and validation (2015) group were essentially the same, except there was a slight drop in hospital length of stay (from a median of 4 days to 3 days) between the 2 periods.
Patient and hospital covariates importantly influenced the daily conditional probability of discharge (Figure 1). Patients admitted to the obstetrics/gynecology department were notably more likely to be discharged from hospital with no influence from the day of week. In contrast, the probability of discharge decreased notably on the weekends in the other departments. Patients on the ward were much more likely to be discharged than those in the intensive care unit, with increasing age associated with a decreased discharge likelihood in the former but not the latter patients. Finally, discharge probabilities varied only slightly between campuses at our hospital with discharge risk decreasing as severity of illness (as measured by LAPS) increased.
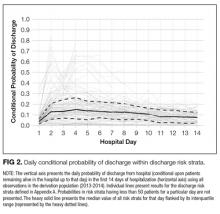
The TEND model contained 142 discharge risk strata (Appendix A). Weekend-holiday status had the strongest association with discharge probability (ie, it was the first splitting variable). The most complex discharge risk strata contained 6 covariates. The daily conditional probability of discharge during the first 2 weeks of hospitalization varied extensively between discharge risk strata (Figure 2). Overall, the conditional discharge probability increased from the first to the second day, remained relatively stable for several days, and then slowly decreased over time. However, this pattern and day-to-day variability differed extensively between risk strata.
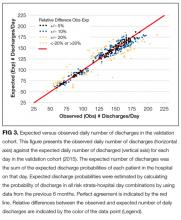
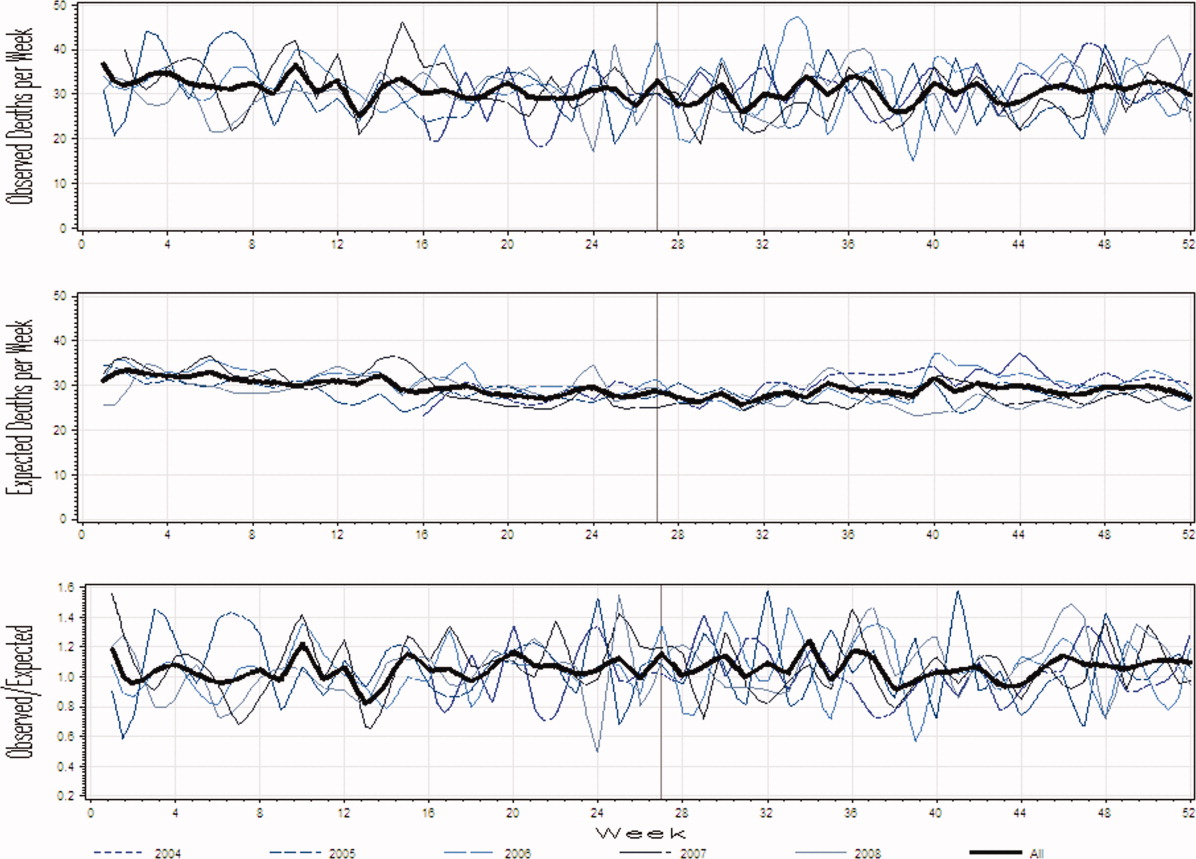
The observed daily number of discharges in the validation cohort varied extensively (median 139; interquartile range [IQR] 95-160; range 39-214). The TEND model accurately predicted the daily number of discharges with the expected daily number being strongly associated with the observed number (adjusted R2 = 89.2%; P < 0.0001; Figure 3). Calibration decreased but remained significant when we limited the analyses by hospital campus (General: R2 = 46.3%; P < 0.0001; Civic: R2 = 47.9%; P < 0.0001; Heart Institute: R2 = 18.1%; P < 0.0001). The expected number of daily discharges was an unbiased estimator of the observed number of discharges (its parameter estimate in a linear regression model with the observed number of discharges as the outcome variable was 1.0005; 95% confidence interval, 0.9647-1.0363). The absolute difference in the observed and expected daily number of discharges was small (median 1.6; IQR −6.8 to 9.4; range −37 to 63.4) as was the relative difference (median 1.4%; IQR −5.5% to 7.1%; range −40.9% to 43.4%). The expected number of discharges was within 20% of the observed number of discharges in 95.1% of days in 2015.
DISCUSSION
Knowing how many patients will soon be discharged from the hospital should greatly facilitate hospital planning. This study showed that the TEND model used simple patient and hospitalization covariates to accurately predict the number of patients who will be discharged from hospital in the next day.
We believe that this study has several notable findings. First, we think that using a nonparametric approach to predicting the daily number of discharges importantly increased accuracy. This approach allowed us to generate expected likelihoods based on actual discharge probabilities at our hospital in the most recent 6 months of hospitalization-days within patients having discharge patterns that were very similar to the patient in question (ie, discharge risk strata, Appendix A). This ensured that trends in hospitalization habits were accounted for without the need of a period variable in our model. In addition, the lack of parameters in the model will make it easier to transplant it to other hospitals. Second, we think that the accuracy of the predictions were remarkable given the relative “crudeness” of our predictors. By using relatively simple factors, the TEND model was able to output accurate predictions for the number of daily discharges (Figure 3).
This study joins several others that have attempted to accomplish the difficult task of predicting the number of hospital discharges by using digitized data. Barnes et al.11 created a model using regression random forest methods in a single medical service within a hospital to predict the daily number of discharges with impressive accuracy (mean daily number of discharges observed 8.29, expected 8.51). Interestingly, the model in this study was more accurate at predicting discharge likelihood than physicians. Levin et al.12 derived a model using discrete time logistic regression to predict the likelihood of discharge from a pediatric intensive care unit, finding that physician orders (captured via electronic order entry) could be categorized and used to significantly increase the accuracy of discharge likelihood. This study demonstrates the potential opportunities within health-related data from hospital data warehouses to improve prediction. We believe that continued work in this field will result in the increased use of digital data to help hospital administrators manage patient beds more efficiently and effectively than currently used resource intensive manual methods.13,14
Several issues should be kept in mind when interpreting our findings. First, our analysis is limited to a single institution in Canada. It will be important to determine if the TEND model methodology generalizes to other hospitals in different jurisdictions. Such an external validation, especially in multiple hospitals, will be important to show that the TEND model methodology works in other facilities. Hospitals could implement the TEND model if they are able to record daily values for each of the variables required to assign patients to a discharge risk stratum (Appendix A) and calculate within each the daily probability of discharge. Hospitals could derive their own discharge risk strata to account for covariates, which we did not include in our study but could be influential, such as insurance status. These discharge risk estimates could also be incorporated into the electronic medical record or hospital dashboards (as long as the data required to generate the estimates are available). These interventions would permit the expected number of hospital discharges (and even the patient-level probability of discharge) to be calculated on a daily basis. Second, 2 potential biases could have influenced the identification of our discharge risk strata (Appendix A). In this process, we used survival tree methods to separate patient-days into clusters having progressively more homogenous discharge patterns. Each split was determined by using a proportional hazards model that ignored the competing risks of death in hospital. In addition, the model expressed age and LAPS as continuous variables, whereas these covariates had to be categorized to create our risk strata groupings. The strength of a covariate’s association with an outcome will decrease when a continuous variable is categorized.15 Both of these issues might have biased our final risk strata categorization (Appendix A). Third, we limited our model to include simple covariates whose values could be determined relatively easily within most hospital administrative data systems. While this increases the generalizability to other hospital information systems, we believe that the introduction of other covariates to the model—such as daily vital signs, laboratory results, medications, or time from operations—could increase prediction accuracy. Finally, it is uncertain whether or not knowing the predicted number of discharges will improve the efficiency of bed management within the hospital. It seems logical that an accurate prediction of the number of beds that will be made available in the next day should improve decisions regarding the number of patients who could be admitted electively to the hospital. It remains to be seen, however, whether this truly happens.
In summary, we found that the TEND model used a handful of patient and hospitalization factors to accurately predict the expected number of discharges from hospital in the next day. Further work is required to implement this model into our institution’s data warehouse and then determine whether this prediction will improve the efficiency of bed management at our hospital.
Disclosure: CvW is supported by a University of Ottawa Department of Medicine Clinician Scientist Chair. The authors have no conflicts of interest
1. Austin PC, Rothwell DM, Tu JV. A comparison of statistical modeling strategies for analyzing length of stay after CABG surgery. Health Serv Outcomes Res Methodol. 2002;3:107-133.
2. Moran JL, Solomon PJ. A review of statistical estimators for risk-adjusted length of stay: analysis of the Australian and new Zealand intensive care adult patient data-base, 2008-2009. BMC Med Res Methodol. 2012;12:68. PubMed
3. Verburg IWM, de Keizer NF, de Jonge E, Peek N. Comparison of regression methods for modeling intensive care length of stay. PLoS One. 2014;9:e109684. PubMed
4. Beyersmann J, Schumacher M. Time-dependent covariates in the proportional subdistribution hazards model for competing risks. Biostatistics. 2008;9:765-776. PubMed
5. Latouche A, Porcher R, Chevret S. A note on including time-dependent covariate in regression model for competing risks data. Biom J. 2005;47:807-814. PubMed
6. Fitzmaurice GM, Laird NM, Ware JH. Marginal models: generalized estimating equations. Applied Longitudinal Analysis. 2nd ed. John Wiley & Sons; 2011;353-394.
7. Escobar GJ, Greene JD, Scheirer P, Gardner MN, Draper D, Kipnis P. Risk-adjusting hospital inpatient mortality using automated inpatient, outpatient, and laboratory databases. Med Care. 2008;46:232-239. PubMed
8. van Walraven C, Escobar GJ, Greene JD, Forster AJ. The Kaiser Permanente inpatient risk adjustment methodology was valid in an external patient population. J Clin Epidemiol. 2010;63:798-803. PubMed
9. Bou-Hamad I, Larocque D, Ben-Ameur H. A review of survival trees. Statist Surv. 2011;44-71.
10. van Walraven C, Bell CM. Risk of death or readmission among people discharged from hospital on Fridays. CMAJ. 2002;166:1672-1673. PubMed
11. Barnes S, Hamrock E, Toerper M, Siddiqui S, Levin S. Real-time prediction of inpatient length of stay for discharge prioritization. J Am Med Inform Assoc. 2016;23:e2-e10. PubMed
12. Levin SRP, Harley ETB, Fackler JCM, et al. Real-time forecasting of pediatric intensive care unit length of stay using computerized provider orders. Crit Care Med. 2012;40:3058-3064. PubMed
13. Resar R, Nolan K, Kaczynski D, Jensen K. Using real-time demand capacity management to improve hospitalwide patient flow. Jt Comm J Qual Patient Saf. 2011;37:217-227. PubMed
14. de Grood A, Blades K, Pendharkar SR. A review of discharge prediction processes in acute care hospitals. Healthc Policy. 2016;12:105-115. PubMed
15. van Walraven C, Hart RG. Leave ‘em alone - why continuous variables should be analyzed as such. Neuroepidemiology 2008;30:138-139. PubMed
Hospitals typically allocate beds based on historical patient volumes. If funding decreases, hospitals will usually try to maximize resource utilization by allocating beds to attain occupancies close to 100% for significant periods of time. This will invariably cause days in which hospital occupancy exceeds capacity, at which time critical entry points (such as the emergency department and operating room) will become blocked. This creates significant concerns over the patient quality of care.
Hospital administrators have very few options when hospital occupancy exceeds 100%. They could postpone admissions for “planned” cases, bring in additional staff to increase capacity, or instigate additional methods to increase hospital discharges such as expanding care resources in the community. All options are costly, bothersome, or cannot be actioned immediately. The need for these options could be minimized by enabling hospital administrators to make more informed decisions regarding hospital bed management by knowing the likely number of discharges in the next 24 hours.
Predicting the number of people who will be discharged in the next day can be approached in several ways. One approach would be to calculate each patient’s expected length of stay and then use the variation around that estimate to calculate each day’s discharge probability. Several studies have attempted to model hospital length of stay using a broad assortment of methodologies, but a mechanism to accurately predict this outcome has been elusive1,2 (with Verburg et al.3 concluding in their study’s abstract that “…it is difficult to predict length of stay…”). A second approach would be to use survival analysis methods to generate each patient’s hazard of discharge over time, which could be directly converted to an expected daily risk of discharge. However, this approach is complicated by the concurrent need to include time-dependent covariates and consider the competing risk of death in hospital, which can complicate survival modeling.4,5 A third approach would be the implementation of a longitudinal analysis using marginal models to predict the daily probability of discharge,6 but this method quickly overwhelms computer resources when large datasets are present.
In this study, we decided to use nonparametric models to predict the daily number of hospital discharges. We first identified patient groups with distinct discharge patterns. We then calculated the conditional daily discharge probability of patients in each of these groups. Finally, these conditional daily discharge probabilities were then summed for each hospital day to generate the expected number of discharges in the next 24 hours. This paper details the methods we used to create our model and the accuracy of its predictions.
METHODS
Study Setting and Databases Used for Analysis
The study took place at The Ottawa Hospital, a 1000-bed teaching hospital with 3 campuses that is the primary referral center in our region. The study was approved by our local research ethics board.
The Patient Registry Database records the date and time of admission for each patient (defined as the moment that a patient’s admission request is registered in the patient registration) and discharge (defined as the time when the patient’s discharge from hospital was entered into the patient registration) for hospital encounters. Emergency department encounters were also identified in the Patient Registry Database along with admission service, patient age and sex, and patient location throughout the admission. The Laboratory Database records all laboratory studies and results on all patients at the hospital.
Study Cohort
We used the Patient Registry Database to identify all people aged 1 year or more who were admitted to the hospital between January 1, 2013, and December 31, 2015. This time frame was selected to (i) ensure that data were complete; and (ii) complete calendar years of data were available for both derivation (patient-days in 2013-2014) and validation (2015) cohorts. Patients who were observed in the emergency room without admission to hospital were not included.
Study Outcome
The study outcome was the number of patients discharged from the hospital each day. For the analysis, the reference point for each day was 1 second past midnight; therefore, values for time-dependent covariates up to and including midnight were used to predict the number of discharges in the next 24 hours.
Study Covariates
Baseline (ie, time-independent) covariates included patient age and sex, admission service, hospital campus, whether or not the patient was admitted from the emergency department (all determined from the Patient Registry Database), and the Laboratory-based Acute Physiological Score (LAPS). The latter, which was calculated with the Laboratory Database using results for 14 tests (arterial pH, PaCO2, PaO2, anion gap, hematocrit, total white blood cell count, serum albumin, total bilirubin, creatinine, urea nitrogen, glucose, sodium, bicarbonate, and troponin I) measured in the 24-hour time frame preceding hospitalization, was derived by Escobar and colleagues7 to measure severity of illness and was subsequently validated in our hospital.8 The independent association of each laboratory perturbation with risk of death in hospital is reflected by the number of points assigned to each lab value with the total LAPS being the sum of these values. Time-dependent covariates included weekday in hospital and whether or not patients were in the intensive care unit.
Analysis
We used 3 stages to create a model to predict the daily expected number of discharges: we identified discharge risk strata containing patients having similar discharge patterns using data from patients in the derivation cohort (first stage); then, we generated the preliminary probability of discharge by determining the daily discharge probability in each discharge risk strata (second stage); finally, we modified the probability from the second stage based on the weekday and admission service and summed these probabilities to create the expected number of discharges on a particular date (third stage).
The first stage identified discharge risk strata based on the covariates listed above. This was determined by using a survival tree approach9 with proportional hazard regression models to generate the “splits.” These models were offered all covariates listed in the Study Covariates section. Admission service was clustered within 4 departments (obstetrics/gynecology, psychiatry, surgery, and medicine) and day of week was “binarized” into weekday/weekend-holiday (because the use of categorical variables with large numbers of groups can “stunt” regression trees due to small numbers of patients—and, therefore, statistical power—in each subgroup). The proportional hazards model identified the covariate having the strongest association with time to discharge (based on the Wald X2 value divided by the degrees of freedom). This variable was then used to split the cohort into subgroups (with continuous covariates being categorized into quartiles). The proportional hazards model was then repeated in each subgroup (with the previous splitting variable[s] excluded from the model). This process continued until no variable was associated with time to discharge with a P value less than .0001. This survival-tree was then used to cluster all patients into distinct discharge risk strata.
In the second stage, we generated the preliminary probability of discharge for a specific date. This was calculated by assigning all patients in hospital to their discharge risk strata (Appendix). We then measured the probability of discharge on each hospitalization day in all discharge risk strata using data from the previous 180 days (we only used the prior 180 days of data to account for temporal changes in hospital discharge patterns). For example, consider a 75-year-old patient on her third hospital day under obstetrics/gynecology on December 19, 2015 (a Saturday). This patient would be assigned to risk stratum #133 (Appendix A). We then measured the probability of discharge of all patients in this discharge risk stratum hospitalized in the previous 6 months (ie, between June 22, 2015, and December 18, 2015) on each hospital day. For risk stratum #133, the probability of discharge on hospital day 3 was 0.1111; therefore, our sample patient’s preliminary expected discharge probability was 0.1111.
To attain stable daily discharge probability estimates, a minimum of 50 patients per discharge risk stratum-hospitalization day combination was required. If there were less than 50 patients for a particular hospitalization day in a particular discharge risk stratum, we grouped hospitalization days in that risk stratum together until the minimum of 50 patients was collected.
The third (and final) stage accounted for the lack of granularity when we created the discharge risk strata in the first stage. As we mentioned above, admission service was clustered into 4 departments and the day of week was clustered into weekend/weekday. However, important variations in discharge probabilities could still exist within departments and between particular days of the week.10 Therefore, we created a correction factor to adjust the preliminary expected number of discharges based on the admission division and day of week. This correction factor used data from the 180 days prior to the analysis date within which the expected daily number of discharges was calculated (using the methods above). The correction factor was the relative difference between the observed and expected number of discharges within each division-day of week grouping.
For example, to calculate the correction factor for our sample patient presented above (75-year-old patient on hospital day 3 under gynecology on Saturday, December 19, 2015), we measured the observed number of discharges from gynecology on Saturdays between June 22, 2015, and December 18, 2015, (n = 206) and the expected number of discharges (n = 195.255) resulting in a correction factor of (observed-expected)/expected = (195.255-206)/195.206 = 0.05503. Therefore, the final expected discharge probability for our sample patient was 0.1111+0.1111*0.05503=0.1172. The expected number of discharges on a particular date was the preliminary expected number of discharges on that date (generated in the second stage) multiplied by the correction factor for the corresponding division-day or week group.
RESULTS
There were 192,859 admissions involving patients more than 1 year of age that spent at least part of their hospitalization between January 1, 2013, and December 31, 2015 (Table). Patients were middle-aged and slightly female predominant, with about half being admitted from the emergency department. Approximately 80% of admissions were to surgical or medical services. More than 95% of admissions ended with a discharge from the hospital with the remainder ending in a death. Almost 30% of hospitalization days occurred on weekends or holidays. Hospitalizations in the derivation (2013-2014) and validation (2015) group were essentially the same, except there was a slight drop in hospital length of stay (from a median of 4 days to 3 days) between the 2 periods.
Patient and hospital covariates importantly influenced the daily conditional probability of discharge (Figure 1). Patients admitted to the obstetrics/gynecology department were notably more likely to be discharged from hospital with no influence from the day of week. In contrast, the probability of discharge decreased notably on the weekends in the other departments. Patients on the ward were much more likely to be discharged than those in the intensive care unit, with increasing age associated with a decreased discharge likelihood in the former but not the latter patients. Finally, discharge probabilities varied only slightly between campuses at our hospital with discharge risk decreasing as severity of illness (as measured by LAPS) increased.
The TEND model contained 142 discharge risk strata (Appendix A). Weekend-holiday status had the strongest association with discharge probability (ie, it was the first splitting variable). The most complex discharge risk strata contained 6 covariates. The daily conditional probability of discharge during the first 2 weeks of hospitalization varied extensively between discharge risk strata (Figure 2). Overall, the conditional discharge probability increased from the first to the second day, remained relatively stable for several days, and then slowly decreased over time. However, this pattern and day-to-day variability differed extensively between risk strata.
The observed daily number of discharges in the validation cohort varied extensively (median 139; interquartile range [IQR] 95-160; range 39-214). The TEND model accurately predicted the daily number of discharges with the expected daily number being strongly associated with the observed number (adjusted R2 = 89.2%; P < 0.0001; Figure 3). Calibration decreased but remained significant when we limited the analyses by hospital campus (General: R2 = 46.3%; P < 0.0001; Civic: R2 = 47.9%; P < 0.0001; Heart Institute: R2 = 18.1%; P < 0.0001). The expected number of daily discharges was an unbiased estimator of the observed number of discharges (its parameter estimate in a linear regression model with the observed number of discharges as the outcome variable was 1.0005; 95% confidence interval, 0.9647-1.0363). The absolute difference in the observed and expected daily number of discharges was small (median 1.6; IQR −6.8 to 9.4; range −37 to 63.4) as was the relative difference (median 1.4%; IQR −5.5% to 7.1%; range −40.9% to 43.4%). The expected number of discharges was within 20% of the observed number of discharges in 95.1% of days in 2015.
DISCUSSION
Knowing how many patients will soon be discharged from the hospital should greatly facilitate hospital planning. This study showed that the TEND model used simple patient and hospitalization covariates to accurately predict the number of patients who will be discharged from hospital in the next day.
We believe that this study has several notable findings. First, we think that using a nonparametric approach to predicting the daily number of discharges importantly increased accuracy. This approach allowed us to generate expected likelihoods based on actual discharge probabilities at our hospital in the most recent 6 months of hospitalization-days within patients having discharge patterns that were very similar to the patient in question (ie, discharge risk strata, Appendix A). This ensured that trends in hospitalization habits were accounted for without the need of a period variable in our model. In addition, the lack of parameters in the model will make it easier to transplant it to other hospitals. Second, we think that the accuracy of the predictions were remarkable given the relative “crudeness” of our predictors. By using relatively simple factors, the TEND model was able to output accurate predictions for the number of daily discharges (Figure 3).
This study joins several others that have attempted to accomplish the difficult task of predicting the number of hospital discharges by using digitized data. Barnes et al.11 created a model using regression random forest methods in a single medical service within a hospital to predict the daily number of discharges with impressive accuracy (mean daily number of discharges observed 8.29, expected 8.51). Interestingly, the model in this study was more accurate at predicting discharge likelihood than physicians. Levin et al.12 derived a model using discrete time logistic regression to predict the likelihood of discharge from a pediatric intensive care unit, finding that physician orders (captured via electronic order entry) could be categorized and used to significantly increase the accuracy of discharge likelihood. This study demonstrates the potential opportunities within health-related data from hospital data warehouses to improve prediction. We believe that continued work in this field will result in the increased use of digital data to help hospital administrators manage patient beds more efficiently and effectively than currently used resource intensive manual methods.13,14
Several issues should be kept in mind when interpreting our findings. First, our analysis is limited to a single institution in Canada. It will be important to determine if the TEND model methodology generalizes to other hospitals in different jurisdictions. Such an external validation, especially in multiple hospitals, will be important to show that the TEND model methodology works in other facilities. Hospitals could implement the TEND model if they are able to record daily values for each of the variables required to assign patients to a discharge risk stratum (Appendix A) and calculate within each the daily probability of discharge. Hospitals could derive their own discharge risk strata to account for covariates, which we did not include in our study but could be influential, such as insurance status. These discharge risk estimates could also be incorporated into the electronic medical record or hospital dashboards (as long as the data required to generate the estimates are available). These interventions would permit the expected number of hospital discharges (and even the patient-level probability of discharge) to be calculated on a daily basis. Second, 2 potential biases could have influenced the identification of our discharge risk strata (Appendix A). In this process, we used survival tree methods to separate patient-days into clusters having progressively more homogenous discharge patterns. Each split was determined by using a proportional hazards model that ignored the competing risks of death in hospital. In addition, the model expressed age and LAPS as continuous variables, whereas these covariates had to be categorized to create our risk strata groupings. The strength of a covariate’s association with an outcome will decrease when a continuous variable is categorized.15 Both of these issues might have biased our final risk strata categorization (Appendix A). Third, we limited our model to include simple covariates whose values could be determined relatively easily within most hospital administrative data systems. While this increases the generalizability to other hospital information systems, we believe that the introduction of other covariates to the model—such as daily vital signs, laboratory results, medications, or time from operations—could increase prediction accuracy. Finally, it is uncertain whether or not knowing the predicted number of discharges will improve the efficiency of bed management within the hospital. It seems logical that an accurate prediction of the number of beds that will be made available in the next day should improve decisions regarding the number of patients who could be admitted electively to the hospital. It remains to be seen, however, whether this truly happens.
In summary, we found that the TEND model used a handful of patient and hospitalization factors to accurately predict the expected number of discharges from hospital in the next day. Further work is required to implement this model into our institution’s data warehouse and then determine whether this prediction will improve the efficiency of bed management at our hospital.
Disclosure: CvW is supported by a University of Ottawa Department of Medicine Clinician Scientist Chair. The authors have no conflicts of interest
Hospitals typically allocate beds based on historical patient volumes. If funding decreases, hospitals will usually try to maximize resource utilization by allocating beds to attain occupancies close to 100% for significant periods of time. This will invariably cause days in which hospital occupancy exceeds capacity, at which time critical entry points (such as the emergency department and operating room) will become blocked. This creates significant concerns over the patient quality of care.
Hospital administrators have very few options when hospital occupancy exceeds 100%. They could postpone admissions for “planned” cases, bring in additional staff to increase capacity, or instigate additional methods to increase hospital discharges such as expanding care resources in the community. All options are costly, bothersome, or cannot be actioned immediately. The need for these options could be minimized by enabling hospital administrators to make more informed decisions regarding hospital bed management by knowing the likely number of discharges in the next 24 hours.
Predicting the number of people who will be discharged in the next day can be approached in several ways. One approach would be to calculate each patient’s expected length of stay and then use the variation around that estimate to calculate each day’s discharge probability. Several studies have attempted to model hospital length of stay using a broad assortment of methodologies, but a mechanism to accurately predict this outcome has been elusive1,2 (with Verburg et al.3 concluding in their study’s abstract that “…it is difficult to predict length of stay…”). A second approach would be to use survival analysis methods to generate each patient’s hazard of discharge over time, which could be directly converted to an expected daily risk of discharge. However, this approach is complicated by the concurrent need to include time-dependent covariates and consider the competing risk of death in hospital, which can complicate survival modeling.4,5 A third approach would be the implementation of a longitudinal analysis using marginal models to predict the daily probability of discharge,6 but this method quickly overwhelms computer resources when large datasets are present.
In this study, we decided to use nonparametric models to predict the daily number of hospital discharges. We first identified patient groups with distinct discharge patterns. We then calculated the conditional daily discharge probability of patients in each of these groups. Finally, these conditional daily discharge probabilities were then summed for each hospital day to generate the expected number of discharges in the next 24 hours. This paper details the methods we used to create our model and the accuracy of its predictions.
METHODS
Study Setting and Databases Used for Analysis
The study took place at The Ottawa Hospital, a 1000-bed teaching hospital with 3 campuses that is the primary referral center in our region. The study was approved by our local research ethics board.
The Patient Registry Database records the date and time of admission for each patient (defined as the moment that a patient’s admission request is registered in the patient registration) and discharge (defined as the time when the patient’s discharge from hospital was entered into the patient registration) for hospital encounters. Emergency department encounters were also identified in the Patient Registry Database along with admission service, patient age and sex, and patient location throughout the admission. The Laboratory Database records all laboratory studies and results on all patients at the hospital.
Study Cohort
We used the Patient Registry Database to identify all people aged 1 year or more who were admitted to the hospital between January 1, 2013, and December 31, 2015. This time frame was selected to (i) ensure that data were complete; and (ii) complete calendar years of data were available for both derivation (patient-days in 2013-2014) and validation (2015) cohorts. Patients who were observed in the emergency room without admission to hospital were not included.
Study Outcome
The study outcome was the number of patients discharged from the hospital each day. For the analysis, the reference point for each day was 1 second past midnight; therefore, values for time-dependent covariates up to and including midnight were used to predict the number of discharges in the next 24 hours.
Study Covariates
Baseline (ie, time-independent) covariates included patient age and sex, admission service, hospital campus, whether or not the patient was admitted from the emergency department (all determined from the Patient Registry Database), and the Laboratory-based Acute Physiological Score (LAPS). The latter, which was calculated with the Laboratory Database using results for 14 tests (arterial pH, PaCO2, PaO2, anion gap, hematocrit, total white blood cell count, serum albumin, total bilirubin, creatinine, urea nitrogen, glucose, sodium, bicarbonate, and troponin I) measured in the 24-hour time frame preceding hospitalization, was derived by Escobar and colleagues7 to measure severity of illness and was subsequently validated in our hospital.8 The independent association of each laboratory perturbation with risk of death in hospital is reflected by the number of points assigned to each lab value with the total LAPS being the sum of these values. Time-dependent covariates included weekday in hospital and whether or not patients were in the intensive care unit.
Analysis
We used 3 stages to create a model to predict the daily expected number of discharges: we identified discharge risk strata containing patients having similar discharge patterns using data from patients in the derivation cohort (first stage); then, we generated the preliminary probability of discharge by determining the daily discharge probability in each discharge risk strata (second stage); finally, we modified the probability from the second stage based on the weekday and admission service and summed these probabilities to create the expected number of discharges on a particular date (third stage).
The first stage identified discharge risk strata based on the covariates listed above. This was determined by using a survival tree approach9 with proportional hazard regression models to generate the “splits.” These models were offered all covariates listed in the Study Covariates section. Admission service was clustered within 4 departments (obstetrics/gynecology, psychiatry, surgery, and medicine) and day of week was “binarized” into weekday/weekend-holiday (because the use of categorical variables with large numbers of groups can “stunt” regression trees due to small numbers of patients—and, therefore, statistical power—in each subgroup). The proportional hazards model identified the covariate having the strongest association with time to discharge (based on the Wald X2 value divided by the degrees of freedom). This variable was then used to split the cohort into subgroups (with continuous covariates being categorized into quartiles). The proportional hazards model was then repeated in each subgroup (with the previous splitting variable[s] excluded from the model). This process continued until no variable was associated with time to discharge with a P value less than .0001. This survival-tree was then used to cluster all patients into distinct discharge risk strata.
In the second stage, we generated the preliminary probability of discharge for a specific date. This was calculated by assigning all patients in hospital to their discharge risk strata (Appendix). We then measured the probability of discharge on each hospitalization day in all discharge risk strata using data from the previous 180 days (we only used the prior 180 days of data to account for temporal changes in hospital discharge patterns). For example, consider a 75-year-old patient on her third hospital day under obstetrics/gynecology on December 19, 2015 (a Saturday). This patient would be assigned to risk stratum #133 (Appendix A). We then measured the probability of discharge of all patients in this discharge risk stratum hospitalized in the previous 6 months (ie, between June 22, 2015, and December 18, 2015) on each hospital day. For risk stratum #133, the probability of discharge on hospital day 3 was 0.1111; therefore, our sample patient’s preliminary expected discharge probability was 0.1111.
To attain stable daily discharge probability estimates, a minimum of 50 patients per discharge risk stratum-hospitalization day combination was required. If there were less than 50 patients for a particular hospitalization day in a particular discharge risk stratum, we grouped hospitalization days in that risk stratum together until the minimum of 50 patients was collected.
The third (and final) stage accounted for the lack of granularity when we created the discharge risk strata in the first stage. As we mentioned above, admission service was clustered into 4 departments and the day of week was clustered into weekend/weekday. However, important variations in discharge probabilities could still exist within departments and between particular days of the week.10 Therefore, we created a correction factor to adjust the preliminary expected number of discharges based on the admission division and day of week. This correction factor used data from the 180 days prior to the analysis date within which the expected daily number of discharges was calculated (using the methods above). The correction factor was the relative difference between the observed and expected number of discharges within each division-day of week grouping.
For example, to calculate the correction factor for our sample patient presented above (75-year-old patient on hospital day 3 under gynecology on Saturday, December 19, 2015), we measured the observed number of discharges from gynecology on Saturdays between June 22, 2015, and December 18, 2015, (n = 206) and the expected number of discharges (n = 195.255) resulting in a correction factor of (observed-expected)/expected = (195.255-206)/195.206 = 0.05503. Therefore, the final expected discharge probability for our sample patient was 0.1111+0.1111*0.05503=0.1172. The expected number of discharges on a particular date was the preliminary expected number of discharges on that date (generated in the second stage) multiplied by the correction factor for the corresponding division-day or week group.
RESULTS
There were 192,859 admissions involving patients more than 1 year of age that spent at least part of their hospitalization between January 1, 2013, and December 31, 2015 (Table). Patients were middle-aged and slightly female predominant, with about half being admitted from the emergency department. Approximately 80% of admissions were to surgical or medical services. More than 95% of admissions ended with a discharge from the hospital with the remainder ending in a death. Almost 30% of hospitalization days occurred on weekends or holidays. Hospitalizations in the derivation (2013-2014) and validation (2015) group were essentially the same, except there was a slight drop in hospital length of stay (from a median of 4 days to 3 days) between the 2 periods.
Patient and hospital covariates importantly influenced the daily conditional probability of discharge (Figure 1). Patients admitted to the obstetrics/gynecology department were notably more likely to be discharged from hospital with no influence from the day of week. In contrast, the probability of discharge decreased notably on the weekends in the other departments. Patients on the ward were much more likely to be discharged than those in the intensive care unit, with increasing age associated with a decreased discharge likelihood in the former but not the latter patients. Finally, discharge probabilities varied only slightly between campuses at our hospital with discharge risk decreasing as severity of illness (as measured by LAPS) increased.
The TEND model contained 142 discharge risk strata (Appendix A). Weekend-holiday status had the strongest association with discharge probability (ie, it was the first splitting variable). The most complex discharge risk strata contained 6 covariates. The daily conditional probability of discharge during the first 2 weeks of hospitalization varied extensively between discharge risk strata (Figure 2). Overall, the conditional discharge probability increased from the first to the second day, remained relatively stable for several days, and then slowly decreased over time. However, this pattern and day-to-day variability differed extensively between risk strata.
The observed daily number of discharges in the validation cohort varied extensively (median 139; interquartile range [IQR] 95-160; range 39-214). The TEND model accurately predicted the daily number of discharges with the expected daily number being strongly associated with the observed number (adjusted R2 = 89.2%; P < 0.0001; Figure 3). Calibration decreased but remained significant when we limited the analyses by hospital campus (General: R2 = 46.3%; P < 0.0001; Civic: R2 = 47.9%; P < 0.0001; Heart Institute: R2 = 18.1%; P < 0.0001). The expected number of daily discharges was an unbiased estimator of the observed number of discharges (its parameter estimate in a linear regression model with the observed number of discharges as the outcome variable was 1.0005; 95% confidence interval, 0.9647-1.0363). The absolute difference in the observed and expected daily number of discharges was small (median 1.6; IQR −6.8 to 9.4; range −37 to 63.4) as was the relative difference (median 1.4%; IQR −5.5% to 7.1%; range −40.9% to 43.4%). The expected number of discharges was within 20% of the observed number of discharges in 95.1% of days in 2015.
DISCUSSION
Knowing how many patients will soon be discharged from the hospital should greatly facilitate hospital planning. This study showed that the TEND model used simple patient and hospitalization covariates to accurately predict the number of patients who will be discharged from hospital in the next day.
We believe that this study has several notable findings. First, we think that using a nonparametric approach to predicting the daily number of discharges importantly increased accuracy. This approach allowed us to generate expected likelihoods based on actual discharge probabilities at our hospital in the most recent 6 months of hospitalization-days within patients having discharge patterns that were very similar to the patient in question (ie, discharge risk strata, Appendix A). This ensured that trends in hospitalization habits were accounted for without the need of a period variable in our model. In addition, the lack of parameters in the model will make it easier to transplant it to other hospitals. Second, we think that the accuracy of the predictions were remarkable given the relative “crudeness” of our predictors. By using relatively simple factors, the TEND model was able to output accurate predictions for the number of daily discharges (Figure 3).
This study joins several others that have attempted to accomplish the difficult task of predicting the number of hospital discharges by using digitized data. Barnes et al.11 created a model using regression random forest methods in a single medical service within a hospital to predict the daily number of discharges with impressive accuracy (mean daily number of discharges observed 8.29, expected 8.51). Interestingly, the model in this study was more accurate at predicting discharge likelihood than physicians. Levin et al.12 derived a model using discrete time logistic regression to predict the likelihood of discharge from a pediatric intensive care unit, finding that physician orders (captured via electronic order entry) could be categorized and used to significantly increase the accuracy of discharge likelihood. This study demonstrates the potential opportunities within health-related data from hospital data warehouses to improve prediction. We believe that continued work in this field will result in the increased use of digital data to help hospital administrators manage patient beds more efficiently and effectively than currently used resource intensive manual methods.13,14
Several issues should be kept in mind when interpreting our findings. First, our analysis is limited to a single institution in Canada. It will be important to determine if the TEND model methodology generalizes to other hospitals in different jurisdictions. Such an external validation, especially in multiple hospitals, will be important to show that the TEND model methodology works in other facilities. Hospitals could implement the TEND model if they are able to record daily values for each of the variables required to assign patients to a discharge risk stratum (Appendix A) and calculate within each the daily probability of discharge. Hospitals could derive their own discharge risk strata to account for covariates, which we did not include in our study but could be influential, such as insurance status. These discharge risk estimates could also be incorporated into the electronic medical record or hospital dashboards (as long as the data required to generate the estimates are available). These interventions would permit the expected number of hospital discharges (and even the patient-level probability of discharge) to be calculated on a daily basis. Second, 2 potential biases could have influenced the identification of our discharge risk strata (Appendix A). In this process, we used survival tree methods to separate patient-days into clusters having progressively more homogenous discharge patterns. Each split was determined by using a proportional hazards model that ignored the competing risks of death in hospital. In addition, the model expressed age and LAPS as continuous variables, whereas these covariates had to be categorized to create our risk strata groupings. The strength of a covariate’s association with an outcome will decrease when a continuous variable is categorized.15 Both of these issues might have biased our final risk strata categorization (Appendix A). Third, we limited our model to include simple covariates whose values could be determined relatively easily within most hospital administrative data systems. While this increases the generalizability to other hospital information systems, we believe that the introduction of other covariates to the model—such as daily vital signs, laboratory results, medications, or time from operations—could increase prediction accuracy. Finally, it is uncertain whether or not knowing the predicted number of discharges will improve the efficiency of bed management within the hospital. It seems logical that an accurate prediction of the number of beds that will be made available in the next day should improve decisions regarding the number of patients who could be admitted electively to the hospital. It remains to be seen, however, whether this truly happens.
In summary, we found that the TEND model used a handful of patient and hospitalization factors to accurately predict the expected number of discharges from hospital in the next day. Further work is required to implement this model into our institution’s data warehouse and then determine whether this prediction will improve the efficiency of bed management at our hospital.
Disclosure: CvW is supported by a University of Ottawa Department of Medicine Clinician Scientist Chair. The authors have no conflicts of interest
1. Austin PC, Rothwell DM, Tu JV. A comparison of statistical modeling strategies for analyzing length of stay after CABG surgery. Health Serv Outcomes Res Methodol. 2002;3:107-133.
2. Moran JL, Solomon PJ. A review of statistical estimators for risk-adjusted length of stay: analysis of the Australian and new Zealand intensive care adult patient data-base, 2008-2009. BMC Med Res Methodol. 2012;12:68. PubMed
3. Verburg IWM, de Keizer NF, de Jonge E, Peek N. Comparison of regression methods for modeling intensive care length of stay. PLoS One. 2014;9:e109684. PubMed
4. Beyersmann J, Schumacher M. Time-dependent covariates in the proportional subdistribution hazards model for competing risks. Biostatistics. 2008;9:765-776. PubMed
5. Latouche A, Porcher R, Chevret S. A note on including time-dependent covariate in regression model for competing risks data. Biom J. 2005;47:807-814. PubMed
6. Fitzmaurice GM, Laird NM, Ware JH. Marginal models: generalized estimating equations. Applied Longitudinal Analysis. 2nd ed. John Wiley & Sons; 2011;353-394.
7. Escobar GJ, Greene JD, Scheirer P, Gardner MN, Draper D, Kipnis P. Risk-adjusting hospital inpatient mortality using automated inpatient, outpatient, and laboratory databases. Med Care. 2008;46:232-239. PubMed
8. van Walraven C, Escobar GJ, Greene JD, Forster AJ. The Kaiser Permanente inpatient risk adjustment methodology was valid in an external patient population. J Clin Epidemiol. 2010;63:798-803. PubMed
9. Bou-Hamad I, Larocque D, Ben-Ameur H. A review of survival trees. Statist Surv. 2011;44-71.
10. van Walraven C, Bell CM. Risk of death or readmission among people discharged from hospital on Fridays. CMAJ. 2002;166:1672-1673. PubMed
11. Barnes S, Hamrock E, Toerper M, Siddiqui S, Levin S. Real-time prediction of inpatient length of stay for discharge prioritization. J Am Med Inform Assoc. 2016;23:e2-e10. PubMed
12. Levin SRP, Harley ETB, Fackler JCM, et al. Real-time forecasting of pediatric intensive care unit length of stay using computerized provider orders. Crit Care Med. 2012;40:3058-3064. PubMed
13. Resar R, Nolan K, Kaczynski D, Jensen K. Using real-time demand capacity management to improve hospitalwide patient flow. Jt Comm J Qual Patient Saf. 2011;37:217-227. PubMed
14. de Grood A, Blades K, Pendharkar SR. A review of discharge prediction processes in acute care hospitals. Healthc Policy. 2016;12:105-115. PubMed
15. van Walraven C, Hart RG. Leave ‘em alone - why continuous variables should be analyzed as such. Neuroepidemiology 2008;30:138-139. PubMed
1. Austin PC, Rothwell DM, Tu JV. A comparison of statistical modeling strategies for analyzing length of stay after CABG surgery. Health Serv Outcomes Res Methodol. 2002;3:107-133.
2. Moran JL, Solomon PJ. A review of statistical estimators for risk-adjusted length of stay: analysis of the Australian and new Zealand intensive care adult patient data-base, 2008-2009. BMC Med Res Methodol. 2012;12:68. PubMed
3. Verburg IWM, de Keizer NF, de Jonge E, Peek N. Comparison of regression methods for modeling intensive care length of stay. PLoS One. 2014;9:e109684. PubMed
4. Beyersmann J, Schumacher M. Time-dependent covariates in the proportional subdistribution hazards model for competing risks. Biostatistics. 2008;9:765-776. PubMed
5. Latouche A, Porcher R, Chevret S. A note on including time-dependent covariate in regression model for competing risks data. Biom J. 2005;47:807-814. PubMed
6. Fitzmaurice GM, Laird NM, Ware JH. Marginal models: generalized estimating equations. Applied Longitudinal Analysis. 2nd ed. John Wiley & Sons; 2011;353-394.
7. Escobar GJ, Greene JD, Scheirer P, Gardner MN, Draper D, Kipnis P. Risk-adjusting hospital inpatient mortality using automated inpatient, outpatient, and laboratory databases. Med Care. 2008;46:232-239. PubMed
8. van Walraven C, Escobar GJ, Greene JD, Forster AJ. The Kaiser Permanente inpatient risk adjustment methodology was valid in an external patient population. J Clin Epidemiol. 2010;63:798-803. PubMed
9. Bou-Hamad I, Larocque D, Ben-Ameur H. A review of survival trees. Statist Surv. 2011;44-71.
10. van Walraven C, Bell CM. Risk of death or readmission among people discharged from hospital on Fridays. CMAJ. 2002;166:1672-1673. PubMed
11. Barnes S, Hamrock E, Toerper M, Siddiqui S, Levin S. Real-time prediction of inpatient length of stay for discharge prioritization. J Am Med Inform Assoc. 2016;23:e2-e10. PubMed
12. Levin SRP, Harley ETB, Fackler JCM, et al. Real-time forecasting of pediatric intensive care unit length of stay using computerized provider orders. Crit Care Med. 2012;40:3058-3064. PubMed
13. Resar R, Nolan K, Kaczynski D, Jensen K. Using real-time demand capacity management to improve hospitalwide patient flow. Jt Comm J Qual Patient Saf. 2011;37:217-227. PubMed
14. de Grood A, Blades K, Pendharkar SR. A review of discharge prediction processes in acute care hospitals. Healthc Policy. 2016;12:105-115. PubMed
15. van Walraven C, Hart RG. Leave ‘em alone - why continuous variables should be analyzed as such. Neuroepidemiology 2008;30:138-139. PubMed
© 2018 Society of Hospital Medicine
“July Phenomenon” Revisited
The July Phenomenon is a commonly used term referring to poor hospital‐patient outcomes when inexperienced house‐staff start their postgraduate training in July. In addition to being an interesting observation, the validity of July Phenomenon has policy implications for teaching hospitals and residency training programs.
Twenty‐three published studies have tried to determine whether the arrival of new house‐staff is associated with increased patient mortality (see Supporting Appendix A in the online version of this article).123 While those studies make an important attempt to determine the validity of the July Phenomenon, they have some notable limitations. All but four of these studies2, 4, 6, 16 limited their analysis to patients with a specific diagnosis, within a particular hospital unit, or treated by a particular specialty. Many studies limited data to those from a single hospital.1, 3, 4, 10, 11, 14, 15, 20, 22 Nine studies did not include data from the entire year in their analyses,4, 6, 7, 10, 13, 1517, 23 and one did not include data from multiple years.22 One study conducted its analysis on death counts alone and did not account for the number of hospitalized people at risk.6 Finally, the analysis of several studies controlled for no severity of illness markers,6, 10, 21 whereas that from several other studies contained only crude measures of comorbidity and severity of illness.14
In this study, we analyzed data at our teaching hospital to determine if evidence exists for the July Phenomenon at our center. We used a highly discriminative and well‐calibrated multivariate model to calculate the risk of dying in hospital, and quantify the ratio of observed to expected number of hospital deaths. Using this as our outcome statistic, we determined whether or not our hospital experiences a July Phenomenon.
METHODS
This study was approved by The Ottawa Hospital (TOH) Research Ethics Board.
Study Setting
TOH is a tertiary‐care teaching hospital with two inpatient campuses. The hospital operates within a publicly funded health care system, serves a population of approximately 1.5 million people in Ottawa and Eastern Ontario, treats all major trauma patients for the region, and provides most of the oncological care in the region.
TOH is the primary medical teaching hospital at the University of Ottawa. In 2010, there were 197 residents starting their first year of postgraduate training in one of 29 programs.
Inclusion Criteria
The study period extended from April 15, 2004 to December 31, 2008. We used this start time because our hospital switched to new coding systems for procedures and diagnoses in April 2002. Since these new coding systems contributed to our outcome statistic, we used a very long period (ie, two years) for coding patterns to stabilize to ensure that any changes seen were not a function of coding patterns. We ended our study in December 2008 because this was the last date of complete data at the time we started the analysis.
We included all medical, surgical, and obstetrical patients admitted to TOH during this time except those who were: younger than 15 years old; transferred to or from another acute care hospital; or obstetrical patients hospitalized for routine childbirth. These patients were excluded because they were not part of the multivariate model that we used to calculate risk of death in hospital (discussed below).24 These exclusions accounted for 25.4% of all admissions during the study period (36,820less than 15 years old; 12,931transferred to or from the hospital; and 44,220uncomplicated admission for childbirth).
All data used in this study came from The Ottawa Hospital Data Warehouse (TOHDW). This is a repository of clinical, laboratory, and administrative data originating from the hospital's major operational information systems. TOHDW contains information on patient demographics and diagnoses, as well as procedures and patient transfers between different units or hospital services during the admission.
Primary OutcomeRatio of Observed to Expected Number of Deaths per Week
For each study day, we measured the number of hospital deaths from the patient registration table in TOHDW. This statistic was collated for each week to ensure numeric stability, especially in our subgroup analyses.
We calculated the weekly expected number of hospital deaths using an extension of the Escobar model.24 The Escobar is a logistic regression model that estimated the probability of death in hospital that was derived and internally validated on almost 260,000 hospitalizations at 17 hospitals in the Kaiser Permanente Health Plan. It included six covariates that were measurable at admission including: patient age; patient sex; admission urgency (ie, elective or emergent) and service (ie, medical or surgical); admission diagnosis; severity of acute illness as measured by the Laboratory‐based Acute Physiology Score (LAPS); and chronic comorbidities as measured by the COmorbidity Point Score (COPS). Hospitalizations were grouped by admission diagnosis. The final model had excellent discrimination (c‐statistic 0.88) and calibration (P value of Hosmer Lemeshow statistic for entire cohort 0.66). This model was externally validated in our center with a c‐statistic of 0.901.25
We extended the Escobar model in several ways (Wong et al., Derivation and validation of a model to predict the daily risk of death in hospital, 2010, unpublished work). First, we modified it into a survival (rather than a logistic) model so it could estimate a daily probability of death in hospital. Second, we included the same covariates as Escobar except that we expressed LAPS as a time‐dependent covariate (meaning that the model accounted for changes in its value during the hospitalization). Finally, we included other time‐dependent covariates including: admission to intensive care unit; undergoing significant procedures; and awaiting long‐term care. This model had excellent discrimination (concordance probability of 0.895, 95% confidence interval [CI] 0.8890.902) and calibration.
We used this survival model to estimate the daily risk of death for all patients in the hospital each day. Summing these risks over hospital patients on each day returned the daily number of expected hospital deaths. This was collated per week.
The outcome statistic for this study was the ratio of the observed to expected weekly number of hospital deaths. Ratios exceeding 1 indicate that more deaths were observed than were expected (given the distribution of important covariates in those people during that week). This outcome statistic has several advantages. First, it accounts for the number of patients in the hospital each day. This is important because the number of hospital deaths will increase as the number of people in hospital increase. Second, it accounts for the severity of illness in each patient on each hospital day. This accounts for daily changes in risk of patient death, because calculation of the expected number of deaths per day was done using a multivariate survival model that included time‐dependent covariates. Therefore, each individual's predicted hazard of death (which was summed over the entire hospital to calculate the total expected number of deaths in hospital each day) took into account the latest values of these covariates. Previous analyses only accounted for risk of death at admission.
Expressing Physician Experience
The latent measure26 in all July Phenomenon studies is collective house‐staff physician experience. This is quantified by a surrogate date variable in which July 1the date that new house‐staff start their training in North Americarepresents minimal experience and June 30 represents maximal experience. We expressed collective physician experience on a scale from 0 (minimum experience) on July 1 to 1 (maximum experience) on June 30. A similar approach has been used previously13 and has advantages over the other methods used to capture collective house‐staff experience. In the stratified, incomplete approach,47, 911, 13, 1517 periods with inexperienced house‐staff (eg, July and August) are grouped together and compared to times with experienced house‐staff (eg, May and June), while ignoring all other data. The specification of cut‐points for this stratification is arbitrary and the method ignores large amounts of data. In the stratified, complete approach, periods with inexperienced house‐staff (eg, July and August) are grouped together and compared to all other times of the year.8, 12, 14, 1820, 22 This is potentially less biased because there are no lost data. However, the cut‐point for determining when house‐staff transition from inexperienced to experienced is arbitrary, and the model assumes that the transition is sudden. This is suboptimal because acquisition of experience is a gradual, constant process.
The pattern by which collective physician experience changes between July 1st and June 30th is unknown. We therefore expressed this evolution using five different patterns varying from a linear change to a natural logarithmic change (see Supporting Appendix B in the online version of this article).
Analysis
We first examined for autocorrelation in our outcome variable using Ljung‐Box statistics at lag 6 and 12 in PROC ARIMA (SAS 9.2, Cary, NC). If significant autocorrelation was absent in our data, linear regression modeling was used to associate the ratio of the observed to expected number of weekly deaths (the outcome variable) with the collective first year physician experience (the predictor variable). Time‐series methodology was to be used if significant autocorrelation was present.
In our baseline analysis, we included all hospitalizations together. In stratified analyses, we categorized hospitalizations by admission status (emergent vs elective) and admission service (medicine vs surgery).
RESULTS
Between April 15, 2004 and December 31, 2008, The Ottawa Hospital had a total of 152,017 inpatient admissions and 107,731 same day surgeries (an annual rate of 32,222 and 22,835, respectively; an average daily rate of 88 and 63, respectively) that met our study's inclusion criteria. These 259,748 encounters included 164,318 people. Table 1 provides an overall description of the study population.
| Characteristic | |
|---|---|
| |
| Patients/hospitalizations, n | 164,318/259,748 |
| Deaths in‐hospital, n (%) | 7,679 (3.0) |
| Length of admission in days, median (IQR) | 2 (16) |
| Male, n (%) | 124,848 (48.1) |
| Age at admission, median (IQR) | 60 (4674) |
| Admission type, n (%) | |
| Elective surgical | 136,406 (52.5) |
| Elective nonsurgical | 20,104 (7.7) |
| Emergent surgical | 32,046 (12.3) |
| Emergent nonsurgical | 71,192 (27.4) |
| Elixhauser score, median (IQR) | 0 (04) |
| LAPS at admission, median (IQR) | 0 (015) |
| At least one admission to intensive care unit, n (%) | 7,779 (3.0) |
| At least one alternative level of care episode, n (%) | 6,971 (2.7) |
| At least one PIMR procedure, n (%) | 47,288 (18.2) |
| First PIMR score,* median (IQR) | 2 (52) |
Weekly Deaths: Observed, Expected, and Ratio
Figure 1A presents the observed weekly number of deaths during the study period. There was an average of 31 deaths per week (range 1551). Some large fluctuations in the weekly number of deaths were seen; in 2007, for example, the number of observed deaths went from 21 in week 13 up to 46 in week 15. However, no obvious seasonal trends in the observed weekly number of deaths were seen (Figure 1A, heavy line) nor were trends between years obvious.
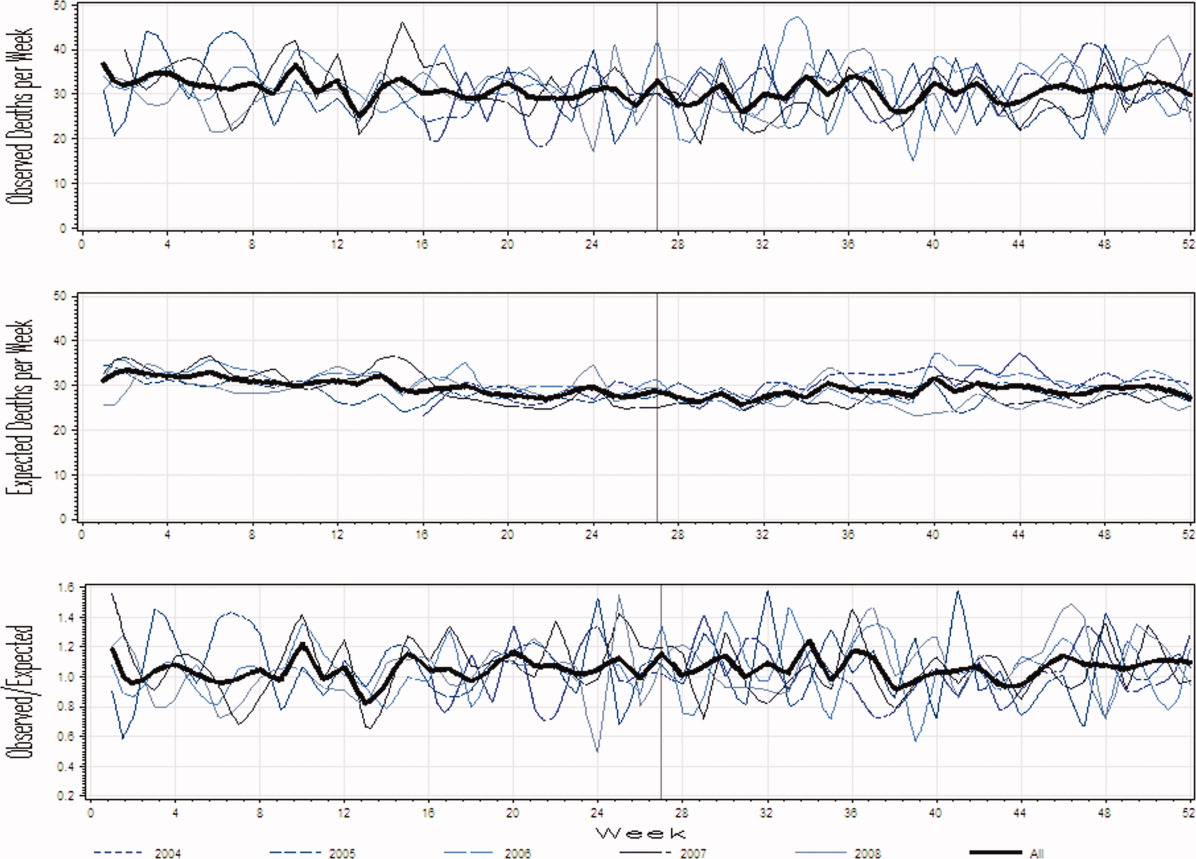
Figure 1B presents the expected weekly number of deaths during the study period. The expected weekly number of deaths averaged 29.6 (range 22.238.7). The expected weekly number of deaths was notably less variable than the observed number of deaths. However, important variations in the expected number of deaths were seen; for example, in 2005, the expected number of deaths increased from 24.1 in week 41 to 29.6 in week 44. Again, we saw no obvious seasonal trends in the expected weekly number of deaths (Figure 1B, heavy line).
Figure 1C illustrates the ratio of observed to the expected weekly number of deaths. The average observed to expected ratio slightly exceeded unity (1.05) and ranged from 0.488 (week 24, in 2008) to 1.821 (week 51, in 2008). We saw no obvious seasonal trends in the ratio of the observed to expected number of weekly deaths. In addition, obvious trends in this ratio were absent over the study period.
Association Between House‐Staff Experience and Death in Hospital
We found no evidence of autocorrelation in the ratio of observed to expected weekly number of deaths. The ratio of observed to expected number of hospital deaths was not significantly associated with house‐staff physician experience (Table 2). This conclusion did not change regardless of which house‐staff physician experience pattern was used in the linear model (Table 2). In addition, our analysis found no significant association between physician experience and patient mortality when analyses were stratified by admission service or admission status (Table 2).
| Patient Population | House‐Staff Experience Pattern (95% CI) | ||||
|---|---|---|---|---|---|
| Linear | Square | Square Root | Cubic | Natural Logarithm | |
| |||||
| All | 0.03 (0.11, 0.06) | 0.02 (0.10, 0.07) | 0.04 (0.15, 0.07) | 0.01 (0.10, 0.08) | 0.05 (0.16, 0.07) |
| Admitting service | |||||
| Medicine | 0.0004 (0.09, 0.10) | 0.01 (0.08, 0.10) | 0.01 (0.13, 0.11) | 0.02 (0.07, 0.11) | 0.03 (0.15, 0.09) |
| Surgery | 0.10 (0.30, 0.10) | 0.11 (0.30, 0.08) | 0.12 (0.37, 0.14) | 0.11 (0.31, 0.08) | 0.09 (0.35, 0.17) |
| Admission status | |||||
| Elective | 0.09 (0.53, 0.35) | 0.10 (0.51, 0.32) | 0.11 (0.66, 0.44) | 0.10 (0.53, 0.33) | 0.11 (0.68, 0.45) |
| Emergent | 0.02 (0.11, 0.07) | 0.01 (0.09, 0.08) | 0.03 (0.14, 0.08) | 0.003 (0.09, 0.09) | 0.04 (0.16, 0.08) |
DISCUSSION
It is natural to suspect that physician experience influences patient outcomes. The commonly discussed July Phenomenon explores changes in teaching‐hospital patient outcomes by time of the academic year. This serves as an ecological surrogate for the latent variable of overall house‐staff experience. Our study used a detailed outcomethe ratio of observed to the expected number of weekly hospital deathsthat adjusted for patient severity of illness. We also modeled collective physician experience using a broad range of patterns. We found no significant variation in mortality rates during the academic year; therefore, the risk of death in hospital does not vary by house‐staff experience at our hospital. This is no evidence of a July Phenomenon for mortality at our center.
We were not surprised that the arrival of inexperienced house‐staff did not significantly change patient mortality for several reasons. First year residents are but one group of treating physicians in a teaching hospital. They are surrounded by many other, more experienced physicians who also contribute to patient care and their outcomes. Given these other physicians, the influence that the relatively smaller number of first year residents have on patient outcomes will be minimized. In addition, the role that these more experienced physicians play in patient care will vary by the experience and ability of residents. The influence of new and inexperienced house‐staff in July will be blunted by an increased role played by staff‐people, fellows, and more experienced house‐staff at that time.
Our study was a methodologically rigorous examination of the July Phenomenon. We used a reliable outcome statisticthe ratio of observed to expected weekly number of hospital deathsthat was created with a validated, discriminative, and well‐calibrated model which predicted risk of death in hospital (Wong et al., Derivation and validation of a model to predict the daily risk of death in hospital, 2010, unpublished work). This statistic is inherently understandable and controlled for patient severity of illness. In addition, our study included a very broad and inclusive group of patients over five years at two hospitals.
Twenty‐three other studies have quantitatively sought a July Phenomenon for patient mortality (see Supporting Appendix A in the online version of this article). The studies contained a broad assortment of research methodologies, patient populations, and analytical methodologies. Nineteen of these studies (83%) found no evidence of a July Phenomenon for teaching‐hospital mortality. In contrast, two of these studies found notable adjusted odds ratios for death in hospital (1.41 and 1.34) in patients undergoing either general surgery13 or complex cardiovascular surgery,19 respectively. Blumberg22 also found an increased risk of death in surgical patients in July, but used indirect standardized mortality ratios as the outcome statistic and was based on only 139 cases at Maryland teaching hospitals in 1984. Only Jen et al.16 showed an increased risk of hospital death with new house‐staff in a broad patient population. However, this study was restricted to two arbitrarily chosen days (one before and one after house‐staff change‐over) and showed an increased risk of hospital death (adjusted OR 1.05, 95% CI 1.001.15) whose borderline statistical significance could have been driven by the large sample size of the study (n = 299,741).
Therefore, the vast majority of dataincluding those presented in our analysesshow that the risk of teaching‐hospital death does not significantly increase with the arrival of new house‐staff. This prompts the question as to why the July Phenomenon is commonly presented in popular media as a proven fact.2733 We believe this is likely because the concept of the July Phenomenon is understandable and has a rather morbid attraction to people, both inside and outside of the medical profession. Given the large amount of data refuting the true existence of a July Phenomenon for patient mortality (see Supporting Appendix A in the online version of this article), we believe that this term should only be used only as an example of an interesting idea that is refuted by a proper analysis of the data.
Several limitations of our study are notable. First, our analysis is limited to a single center, albeit with two hospitals. However, ours is one of the largest teaching centers in Canada with many new residents each year. Second, we only examined the association of physician experience on hospital mortality. While it is possible that physician experience significantly influences other patient outcomes, mortality is, obviously, an important and reliably tallied statistic that is used as the primary outcome in most July Phenomenon studies. Third, we excluded approximately a quarter of all hospitalizations from the study. These exclusions were necessary because the Escobar model does not apply to these people and can therefore not be used to predict their risk of death in hospital. However, the vast majority of excluded patients (those less than 15 years old, and women admitted for routine childbirth) have a very low risk of death (the former because they are almost exclusively newborns, and the latter because the risk of maternal death during childbirth is very low). Since these people will contribute very little to either the expected or observed number of deaths, their exclusion will do little to threaten the study's validity. The remaining patients who were transferred to or from other hospitals (n = 12,931) makes a small proportion of the total sampling frame (5% of admissions). Fourth, our study did not identify any significant association between house‐staff experience and patient mortality (Table 2). However, the confidence intervals around our estimates are wide enough, especially in some subgroups such as patients admitted electively, that important changes in patient mortality with house‐staff experience cannot be excluded. For example, whereas our study found that a decrease in the ratio of observed to expected number of deaths exceeding 30% is very unlikely, it is still possible that this decrease is up to 30% (the lower range of the confidence interval in Table 2). However, using this logic, it could also increase by up to 10% (Table 2). Finally, we did not directly measure individual physician experience. New residents can vary extensively in their individual experience and ability. Incorporating individual physician measures of experience and ability would more reliably let us measure the association of new residents with patient outcomes. Without this, we had to rely on an ecological measure of physician experiencenamely calendar date. Again, this method is an industry standard since all studies quantify physician experience ecologically by date (see Supporting Appendix A in the online version of this article).
In summary, our datasimilar to most studies on this topicshow that the risk of death in teaching hospitals does not change with the arrival of new house‐staff.
- ,,.The effects of scheduled intern rotation on the cost and quality of teaching hospital care.Eval Health Prof.1994;17:259–272.
- ,,,.Specialty differences in the “July Phenomenon” for Twin Cities teaching hospitals.Med Care.1993;31:73–83.
- ,,,.The relationship of house staff experience to the cost and quality of inpatient care.JAMA.1990;263:953–957.
- ,,,.Indirect costs for medical education. Is there a July phenomenon?Arch Intern Med.1989;149:765–768.
- ,,,,.The impact of accreditation council for graduate medical education duty hours, the July phenomenon, and hospital teaching status on stroke outcomes.J Stroke Cerebrovasc Dis.2009;18:232–238.
- ,.The killing season—Fact or fiction.BMJ1994;309:1690.
- ,,, et al.The July effect: Impact of the beginning of the academic cycle on cardiac surgical outcomes in a cohort of 70,616 patients.Ann Thorac Surg.2009;88:70–75.
- ,.Is there a July phenomenon? The effect of July admission on intensive care mortality and length of stay in teaching hospitals.J Gen Intern Med.2003;18:639–645.
- ,,,.Neonatal mortality among low birth weight infants during the initial months of the academic year.J Perinatol.2008;28:691–695.
- ,,,,.The “July Phenomenon” and the care of the severely injured patient: Fact or fiction?Surgery.2001;130:346–353.
- ,,, et al.The July effect and cardiac surgery: The effect of the beginning of the academic cycle on outcomes.Am J Surg.2008;196:720–725.
- ,,,.Mortality in Medicare patients undergoing surgery in July in teaching hospitals.Ann Surg.2009;249:871–876.
- ,,, et al.Seasonal variation in surgical outcomes as measured by the American College of Surgeons–National Surgical Quality Improvement Program (ACS‐NSQIP).Ann Surg.2007;246:456–465.
- ,,, et al.Mortality rate and length of stay of patients admitted to the intensive care unit in July.Crit Care Med.2004;32:1161–1165.
- ,,,,,.July—As good a time as any to be injured.J Trauma‐Injury Infect Crit Care.2009;67:1087–1090.
- ,,,,.Early in‐hospital mortality following trainee doctors' first day at work.PLoS ONE.2009;4.
- ,,.Effect of critical care medicine fellows on patient outcome in the intensive care unit.Acad Med.2006;81:S1–S4.
- ,,,,.The “July Phenomenon”: Is trauma the exception?J Am Coll Surg.2009;209:378–384.
- ,,.Impact of cardiothoracic resident turnover on mortality after cardiac surgery: A dynamic human factor.Ann Thorac Surg.2008;86:123–131.
- ,,.Is there a “July Phenomenon” in pediatric neurosurgery at teaching hospitals?J Neurosurg Pediatr.2006;105:169–176.
- ,,,,.Mortality and morbidity by month of birth of neonates admitted to an academic neonatal intensive care unit.Pediatrics.2008;122:E1048–E1052.
- .Measuring surgical quality in Maryland: A model.Health Aff.1988;7:62–78.
- ,,, et al.Complications and death at the start of the new academic year: Is there a July phenomenon?J Trauma‐Injury Infect Crit Care.2010;68(1):19–22.
- ,,,,,.Risk‐adjusting hospital inpatient mortality using automated inpatient, outpatient, and laboratory databases.Med Care.2008;46:232–239.
- ,,,.The Kaiser Permanente inpatient risk adjustment methodology was valid in an external patient population.J Clin Epidemiol.2010;63:798–803.
- .Introduction: The logic of latent variables.Latent Class Analysis.Newbury Park, CA:Sage;1987:5–10.
- July Effect. Wikipedia. Available at: http://en.wikipedia.org/wiki/July_effect. Accessed April 1,2011.
- Study proves “killing season” occurs as new doctors start work. September 23,2010. Herald Scotland. Available at: http://www.heraldscotland.com/news/health/study‐proves‐killing‐season‐occurs‐as‐new‐doctors‐start‐work‐1.921632. Accessed April 1, 2011.
- The “July effect”: Worst month for fatal hospital errors, study finds. June 3,2010. ABC News. Available at: http://abcnews.go.com/WN/WellnessNews/july‐month‐fatal‐hospital‐errors‐study‐finds/story?id=10819652. Accessed 1 April, 2011.
- “Deaths rise” with junior doctors. September 22,2010. BBC News. Available at: http://news.bbc.co.uk/2/hi/health/8269729.stm. Accessed April 1, 2011.
- .July: When not to go to the hospital. June 2,2010. Science News. Available at: http://www.sciencenews.org/view/generic/id/59865/title/July_When_not_to_go_to_the_hospital. Accessed April 1, 2011.
- July: A deadly time for hospitals. July 5,2010. National Public Radio. Available at: http://www.npr.org/templates/story/story.php?storyId=128321489. Accessed April 1, 2011.
- .Medical errors and patient safety: Beware the “July effect.” June 4,2010. Better Health. Available at: http://getbetterhealth.com/medical‐errors‐and‐patient‐safety‐beware‐of‐the‐july‐effect/2010.06.04. Accessed April 1, 2011.
The July Phenomenon is a commonly used term referring to poor hospital‐patient outcomes when inexperienced house‐staff start their postgraduate training in July. In addition to being an interesting observation, the validity of July Phenomenon has policy implications for teaching hospitals and residency training programs.
Twenty‐three published studies have tried to determine whether the arrival of new house‐staff is associated with increased patient mortality (see Supporting Appendix A in the online version of this article).123 While those studies make an important attempt to determine the validity of the July Phenomenon, they have some notable limitations. All but four of these studies2, 4, 6, 16 limited their analysis to patients with a specific diagnosis, within a particular hospital unit, or treated by a particular specialty. Many studies limited data to those from a single hospital.1, 3, 4, 10, 11, 14, 15, 20, 22 Nine studies did not include data from the entire year in their analyses,4, 6, 7, 10, 13, 1517, 23 and one did not include data from multiple years.22 One study conducted its analysis on death counts alone and did not account for the number of hospitalized people at risk.6 Finally, the analysis of several studies controlled for no severity of illness markers,6, 10, 21 whereas that from several other studies contained only crude measures of comorbidity and severity of illness.14
In this study, we analyzed data at our teaching hospital to determine if evidence exists for the July Phenomenon at our center. We used a highly discriminative and well‐calibrated multivariate model to calculate the risk of dying in hospital, and quantify the ratio of observed to expected number of hospital deaths. Using this as our outcome statistic, we determined whether or not our hospital experiences a July Phenomenon.
METHODS
This study was approved by The Ottawa Hospital (TOH) Research Ethics Board.
Study Setting
TOH is a tertiary‐care teaching hospital with two inpatient campuses. The hospital operates within a publicly funded health care system, serves a population of approximately 1.5 million people in Ottawa and Eastern Ontario, treats all major trauma patients for the region, and provides most of the oncological care in the region.
TOH is the primary medical teaching hospital at the University of Ottawa. In 2010, there were 197 residents starting their first year of postgraduate training in one of 29 programs.
Inclusion Criteria
The study period extended from April 15, 2004 to December 31, 2008. We used this start time because our hospital switched to new coding systems for procedures and diagnoses in April 2002. Since these new coding systems contributed to our outcome statistic, we used a very long period (ie, two years) for coding patterns to stabilize to ensure that any changes seen were not a function of coding patterns. We ended our study in December 2008 because this was the last date of complete data at the time we started the analysis.
We included all medical, surgical, and obstetrical patients admitted to TOH during this time except those who were: younger than 15 years old; transferred to or from another acute care hospital; or obstetrical patients hospitalized for routine childbirth. These patients were excluded because they were not part of the multivariate model that we used to calculate risk of death in hospital (discussed below).24 These exclusions accounted for 25.4% of all admissions during the study period (36,820less than 15 years old; 12,931transferred to or from the hospital; and 44,220uncomplicated admission for childbirth).
All data used in this study came from The Ottawa Hospital Data Warehouse (TOHDW). This is a repository of clinical, laboratory, and administrative data originating from the hospital's major operational information systems. TOHDW contains information on patient demographics and diagnoses, as well as procedures and patient transfers between different units or hospital services during the admission.
Primary OutcomeRatio of Observed to Expected Number of Deaths per Week
For each study day, we measured the number of hospital deaths from the patient registration table in TOHDW. This statistic was collated for each week to ensure numeric stability, especially in our subgroup analyses.
We calculated the weekly expected number of hospital deaths using an extension of the Escobar model.24 The Escobar is a logistic regression model that estimated the probability of death in hospital that was derived and internally validated on almost 260,000 hospitalizations at 17 hospitals in the Kaiser Permanente Health Plan. It included six covariates that were measurable at admission including: patient age; patient sex; admission urgency (ie, elective or emergent) and service (ie, medical or surgical); admission diagnosis; severity of acute illness as measured by the Laboratory‐based Acute Physiology Score (LAPS); and chronic comorbidities as measured by the COmorbidity Point Score (COPS). Hospitalizations were grouped by admission diagnosis. The final model had excellent discrimination (c‐statistic 0.88) and calibration (P value of Hosmer Lemeshow statistic for entire cohort 0.66). This model was externally validated in our center with a c‐statistic of 0.901.25
We extended the Escobar model in several ways (Wong et al., Derivation and validation of a model to predict the daily risk of death in hospital, 2010, unpublished work). First, we modified it into a survival (rather than a logistic) model so it could estimate a daily probability of death in hospital. Second, we included the same covariates as Escobar except that we expressed LAPS as a time‐dependent covariate (meaning that the model accounted for changes in its value during the hospitalization). Finally, we included other time‐dependent covariates including: admission to intensive care unit; undergoing significant procedures; and awaiting long‐term care. This model had excellent discrimination (concordance probability of 0.895, 95% confidence interval [CI] 0.8890.902) and calibration.
We used this survival model to estimate the daily risk of death for all patients in the hospital each day. Summing these risks over hospital patients on each day returned the daily number of expected hospital deaths. This was collated per week.
The outcome statistic for this study was the ratio of the observed to expected weekly number of hospital deaths. Ratios exceeding 1 indicate that more deaths were observed than were expected (given the distribution of important covariates in those people during that week). This outcome statistic has several advantages. First, it accounts for the number of patients in the hospital each day. This is important because the number of hospital deaths will increase as the number of people in hospital increase. Second, it accounts for the severity of illness in each patient on each hospital day. This accounts for daily changes in risk of patient death, because calculation of the expected number of deaths per day was done using a multivariate survival model that included time‐dependent covariates. Therefore, each individual's predicted hazard of death (which was summed over the entire hospital to calculate the total expected number of deaths in hospital each day) took into account the latest values of these covariates. Previous analyses only accounted for risk of death at admission.
Expressing Physician Experience
The latent measure26 in all July Phenomenon studies is collective house‐staff physician experience. This is quantified by a surrogate date variable in which July 1the date that new house‐staff start their training in North Americarepresents minimal experience and June 30 represents maximal experience. We expressed collective physician experience on a scale from 0 (minimum experience) on July 1 to 1 (maximum experience) on June 30. A similar approach has been used previously13 and has advantages over the other methods used to capture collective house‐staff experience. In the stratified, incomplete approach,47, 911, 13, 1517 periods with inexperienced house‐staff (eg, July and August) are grouped together and compared to times with experienced house‐staff (eg, May and June), while ignoring all other data. The specification of cut‐points for this stratification is arbitrary and the method ignores large amounts of data. In the stratified, complete approach, periods with inexperienced house‐staff (eg, July and August) are grouped together and compared to all other times of the year.8, 12, 14, 1820, 22 This is potentially less biased because there are no lost data. However, the cut‐point for determining when house‐staff transition from inexperienced to experienced is arbitrary, and the model assumes that the transition is sudden. This is suboptimal because acquisition of experience is a gradual, constant process.
The pattern by which collective physician experience changes between July 1st and June 30th is unknown. We therefore expressed this evolution using five different patterns varying from a linear change to a natural logarithmic change (see Supporting Appendix B in the online version of this article).
Analysis
We first examined for autocorrelation in our outcome variable using Ljung‐Box statistics at lag 6 and 12 in PROC ARIMA (SAS 9.2, Cary, NC). If significant autocorrelation was absent in our data, linear regression modeling was used to associate the ratio of the observed to expected number of weekly deaths (the outcome variable) with the collective first year physician experience (the predictor variable). Time‐series methodology was to be used if significant autocorrelation was present.
In our baseline analysis, we included all hospitalizations together. In stratified analyses, we categorized hospitalizations by admission status (emergent vs elective) and admission service (medicine vs surgery).
RESULTS
Between April 15, 2004 and December 31, 2008, The Ottawa Hospital had a total of 152,017 inpatient admissions and 107,731 same day surgeries (an annual rate of 32,222 and 22,835, respectively; an average daily rate of 88 and 63, respectively) that met our study's inclusion criteria. These 259,748 encounters included 164,318 people. Table 1 provides an overall description of the study population.
| Characteristic | |
|---|---|
| |
| Patients/hospitalizations, n | 164,318/259,748 |
| Deaths in‐hospital, n (%) | 7,679 (3.0) |
| Length of admission in days, median (IQR) | 2 (16) |
| Male, n (%) | 124,848 (48.1) |
| Age at admission, median (IQR) | 60 (4674) |
| Admission type, n (%) | |
| Elective surgical | 136,406 (52.5) |
| Elective nonsurgical | 20,104 (7.7) |
| Emergent surgical | 32,046 (12.3) |
| Emergent nonsurgical | 71,192 (27.4) |
| Elixhauser score, median (IQR) | 0 (04) |
| LAPS at admission, median (IQR) | 0 (015) |
| At least one admission to intensive care unit, n (%) | 7,779 (3.0) |
| At least one alternative level of care episode, n (%) | 6,971 (2.7) |
| At least one PIMR procedure, n (%) | 47,288 (18.2) |
| First PIMR score,* median (IQR) | 2 (52) |
Weekly Deaths: Observed, Expected, and Ratio
Figure 1A presents the observed weekly number of deaths during the study period. There was an average of 31 deaths per week (range 1551). Some large fluctuations in the weekly number of deaths were seen; in 2007, for example, the number of observed deaths went from 21 in week 13 up to 46 in week 15. However, no obvious seasonal trends in the observed weekly number of deaths were seen (Figure 1A, heavy line) nor were trends between years obvious.

Figure 1B presents the expected weekly number of deaths during the study period. The expected weekly number of deaths averaged 29.6 (range 22.238.7). The expected weekly number of deaths was notably less variable than the observed number of deaths. However, important variations in the expected number of deaths were seen; for example, in 2005, the expected number of deaths increased from 24.1 in week 41 to 29.6 in week 44. Again, we saw no obvious seasonal trends in the expected weekly number of deaths (Figure 1B, heavy line).
Figure 1C illustrates the ratio of observed to the expected weekly number of deaths. The average observed to expected ratio slightly exceeded unity (1.05) and ranged from 0.488 (week 24, in 2008) to 1.821 (week 51, in 2008). We saw no obvious seasonal trends in the ratio of the observed to expected number of weekly deaths. In addition, obvious trends in this ratio were absent over the study period.
Association Between House‐Staff Experience and Death in Hospital
We found no evidence of autocorrelation in the ratio of observed to expected weekly number of deaths. The ratio of observed to expected number of hospital deaths was not significantly associated with house‐staff physician experience (Table 2). This conclusion did not change regardless of which house‐staff physician experience pattern was used in the linear model (Table 2). In addition, our analysis found no significant association between physician experience and patient mortality when analyses were stratified by admission service or admission status (Table 2).
| Patient Population | House‐Staff Experience Pattern (95% CI) | ||||
|---|---|---|---|---|---|
| Linear | Square | Square Root | Cubic | Natural Logarithm | |
| |||||
| All | 0.03 (0.11, 0.06) | 0.02 (0.10, 0.07) | 0.04 (0.15, 0.07) | 0.01 (0.10, 0.08) | 0.05 (0.16, 0.07) |
| Admitting service | |||||
| Medicine | 0.0004 (0.09, 0.10) | 0.01 (0.08, 0.10) | 0.01 (0.13, 0.11) | 0.02 (0.07, 0.11) | 0.03 (0.15, 0.09) |
| Surgery | 0.10 (0.30, 0.10) | 0.11 (0.30, 0.08) | 0.12 (0.37, 0.14) | 0.11 (0.31, 0.08) | 0.09 (0.35, 0.17) |
| Admission status | |||||
| Elective | 0.09 (0.53, 0.35) | 0.10 (0.51, 0.32) | 0.11 (0.66, 0.44) | 0.10 (0.53, 0.33) | 0.11 (0.68, 0.45) |
| Emergent | 0.02 (0.11, 0.07) | 0.01 (0.09, 0.08) | 0.03 (0.14, 0.08) | 0.003 (0.09, 0.09) | 0.04 (0.16, 0.08) |
DISCUSSION
It is natural to suspect that physician experience influences patient outcomes. The commonly discussed July Phenomenon explores changes in teaching‐hospital patient outcomes by time of the academic year. This serves as an ecological surrogate for the latent variable of overall house‐staff experience. Our study used a detailed outcomethe ratio of observed to the expected number of weekly hospital deathsthat adjusted for patient severity of illness. We also modeled collective physician experience using a broad range of patterns. We found no significant variation in mortality rates during the academic year; therefore, the risk of death in hospital does not vary by house‐staff experience at our hospital. This is no evidence of a July Phenomenon for mortality at our center.
We were not surprised that the arrival of inexperienced house‐staff did not significantly change patient mortality for several reasons. First year residents are but one group of treating physicians in a teaching hospital. They are surrounded by many other, more experienced physicians who also contribute to patient care and their outcomes. Given these other physicians, the influence that the relatively smaller number of first year residents have on patient outcomes will be minimized. In addition, the role that these more experienced physicians play in patient care will vary by the experience and ability of residents. The influence of new and inexperienced house‐staff in July will be blunted by an increased role played by staff‐people, fellows, and more experienced house‐staff at that time.
Our study was a methodologically rigorous examination of the July Phenomenon. We used a reliable outcome statisticthe ratio of observed to expected weekly number of hospital deathsthat was created with a validated, discriminative, and well‐calibrated model which predicted risk of death in hospital (Wong et al., Derivation and validation of a model to predict the daily risk of death in hospital, 2010, unpublished work). This statistic is inherently understandable and controlled for patient severity of illness. In addition, our study included a very broad and inclusive group of patients over five years at two hospitals.
Twenty‐three other studies have quantitatively sought a July Phenomenon for patient mortality (see Supporting Appendix A in the online version of this article). The studies contained a broad assortment of research methodologies, patient populations, and analytical methodologies. Nineteen of these studies (83%) found no evidence of a July Phenomenon for teaching‐hospital mortality. In contrast, two of these studies found notable adjusted odds ratios for death in hospital (1.41 and 1.34) in patients undergoing either general surgery13 or complex cardiovascular surgery,19 respectively. Blumberg22 also found an increased risk of death in surgical patients in July, but used indirect standardized mortality ratios as the outcome statistic and was based on only 139 cases at Maryland teaching hospitals in 1984. Only Jen et al.16 showed an increased risk of hospital death with new house‐staff in a broad patient population. However, this study was restricted to two arbitrarily chosen days (one before and one after house‐staff change‐over) and showed an increased risk of hospital death (adjusted OR 1.05, 95% CI 1.001.15) whose borderline statistical significance could have been driven by the large sample size of the study (n = 299,741).
Therefore, the vast majority of dataincluding those presented in our analysesshow that the risk of teaching‐hospital death does not significantly increase with the arrival of new house‐staff. This prompts the question as to why the July Phenomenon is commonly presented in popular media as a proven fact.2733 We believe this is likely because the concept of the July Phenomenon is understandable and has a rather morbid attraction to people, both inside and outside of the medical profession. Given the large amount of data refuting the true existence of a July Phenomenon for patient mortality (see Supporting Appendix A in the online version of this article), we believe that this term should only be used only as an example of an interesting idea that is refuted by a proper analysis of the data.
Several limitations of our study are notable. First, our analysis is limited to a single center, albeit with two hospitals. However, ours is one of the largest teaching centers in Canada with many new residents each year. Second, we only examined the association of physician experience on hospital mortality. While it is possible that physician experience significantly influences other patient outcomes, mortality is, obviously, an important and reliably tallied statistic that is used as the primary outcome in most July Phenomenon studies. Third, we excluded approximately a quarter of all hospitalizations from the study. These exclusions were necessary because the Escobar model does not apply to these people and can therefore not be used to predict their risk of death in hospital. However, the vast majority of excluded patients (those less than 15 years old, and women admitted for routine childbirth) have a very low risk of death (the former because they are almost exclusively newborns, and the latter because the risk of maternal death during childbirth is very low). Since these people will contribute very little to either the expected or observed number of deaths, their exclusion will do little to threaten the study's validity. The remaining patients who were transferred to or from other hospitals (n = 12,931) makes a small proportion of the total sampling frame (5% of admissions). Fourth, our study did not identify any significant association between house‐staff experience and patient mortality (Table 2). However, the confidence intervals around our estimates are wide enough, especially in some subgroups such as patients admitted electively, that important changes in patient mortality with house‐staff experience cannot be excluded. For example, whereas our study found that a decrease in the ratio of observed to expected number of deaths exceeding 30% is very unlikely, it is still possible that this decrease is up to 30% (the lower range of the confidence interval in Table 2). However, using this logic, it could also increase by up to 10% (Table 2). Finally, we did not directly measure individual physician experience. New residents can vary extensively in their individual experience and ability. Incorporating individual physician measures of experience and ability would more reliably let us measure the association of new residents with patient outcomes. Without this, we had to rely on an ecological measure of physician experiencenamely calendar date. Again, this method is an industry standard since all studies quantify physician experience ecologically by date (see Supporting Appendix A in the online version of this article).
In summary, our datasimilar to most studies on this topicshow that the risk of death in teaching hospitals does not change with the arrival of new house‐staff.
The July Phenomenon is a commonly used term referring to poor hospital‐patient outcomes when inexperienced house‐staff start their postgraduate training in July. In addition to being an interesting observation, the validity of July Phenomenon has policy implications for teaching hospitals and residency training programs.
Twenty‐three published studies have tried to determine whether the arrival of new house‐staff is associated with increased patient mortality (see Supporting Appendix A in the online version of this article).123 While those studies make an important attempt to determine the validity of the July Phenomenon, they have some notable limitations. All but four of these studies2, 4, 6, 16 limited their analysis to patients with a specific diagnosis, within a particular hospital unit, or treated by a particular specialty. Many studies limited data to those from a single hospital.1, 3, 4, 10, 11, 14, 15, 20, 22 Nine studies did not include data from the entire year in their analyses,4, 6, 7, 10, 13, 1517, 23 and one did not include data from multiple years.22 One study conducted its analysis on death counts alone and did not account for the number of hospitalized people at risk.6 Finally, the analysis of several studies controlled for no severity of illness markers,6, 10, 21 whereas that from several other studies contained only crude measures of comorbidity and severity of illness.14
In this study, we analyzed data at our teaching hospital to determine if evidence exists for the July Phenomenon at our center. We used a highly discriminative and well‐calibrated multivariate model to calculate the risk of dying in hospital, and quantify the ratio of observed to expected number of hospital deaths. Using this as our outcome statistic, we determined whether or not our hospital experiences a July Phenomenon.
METHODS
This study was approved by The Ottawa Hospital (TOH) Research Ethics Board.
Study Setting
TOH is a tertiary‐care teaching hospital with two inpatient campuses. The hospital operates within a publicly funded health care system, serves a population of approximately 1.5 million people in Ottawa and Eastern Ontario, treats all major trauma patients for the region, and provides most of the oncological care in the region.
TOH is the primary medical teaching hospital at the University of Ottawa. In 2010, there were 197 residents starting their first year of postgraduate training in one of 29 programs.
Inclusion Criteria
The study period extended from April 15, 2004 to December 31, 2008. We used this start time because our hospital switched to new coding systems for procedures and diagnoses in April 2002. Since these new coding systems contributed to our outcome statistic, we used a very long period (ie, two years) for coding patterns to stabilize to ensure that any changes seen were not a function of coding patterns. We ended our study in December 2008 because this was the last date of complete data at the time we started the analysis.
We included all medical, surgical, and obstetrical patients admitted to TOH during this time except those who were: younger than 15 years old; transferred to or from another acute care hospital; or obstetrical patients hospitalized for routine childbirth. These patients were excluded because they were not part of the multivariate model that we used to calculate risk of death in hospital (discussed below).24 These exclusions accounted for 25.4% of all admissions during the study period (36,820less than 15 years old; 12,931transferred to or from the hospital; and 44,220uncomplicated admission for childbirth).
All data used in this study came from The Ottawa Hospital Data Warehouse (TOHDW). This is a repository of clinical, laboratory, and administrative data originating from the hospital's major operational information systems. TOHDW contains information on patient demographics and diagnoses, as well as procedures and patient transfers between different units or hospital services during the admission.
Primary OutcomeRatio of Observed to Expected Number of Deaths per Week
For each study day, we measured the number of hospital deaths from the patient registration table in TOHDW. This statistic was collated for each week to ensure numeric stability, especially in our subgroup analyses.
We calculated the weekly expected number of hospital deaths using an extension of the Escobar model.24 The Escobar is a logistic regression model that estimated the probability of death in hospital that was derived and internally validated on almost 260,000 hospitalizations at 17 hospitals in the Kaiser Permanente Health Plan. It included six covariates that were measurable at admission including: patient age; patient sex; admission urgency (ie, elective or emergent) and service (ie, medical or surgical); admission diagnosis; severity of acute illness as measured by the Laboratory‐based Acute Physiology Score (LAPS); and chronic comorbidities as measured by the COmorbidity Point Score (COPS). Hospitalizations were grouped by admission diagnosis. The final model had excellent discrimination (c‐statistic 0.88) and calibration (P value of Hosmer Lemeshow statistic for entire cohort 0.66). This model was externally validated in our center with a c‐statistic of 0.901.25
We extended the Escobar model in several ways (Wong et al., Derivation and validation of a model to predict the daily risk of death in hospital, 2010, unpublished work). First, we modified it into a survival (rather than a logistic) model so it could estimate a daily probability of death in hospital. Second, we included the same covariates as Escobar except that we expressed LAPS as a time‐dependent covariate (meaning that the model accounted for changes in its value during the hospitalization). Finally, we included other time‐dependent covariates including: admission to intensive care unit; undergoing significant procedures; and awaiting long‐term care. This model had excellent discrimination (concordance probability of 0.895, 95% confidence interval [CI] 0.8890.902) and calibration.
We used this survival model to estimate the daily risk of death for all patients in the hospital each day. Summing these risks over hospital patients on each day returned the daily number of expected hospital deaths. This was collated per week.
The outcome statistic for this study was the ratio of the observed to expected weekly number of hospital deaths. Ratios exceeding 1 indicate that more deaths were observed than were expected (given the distribution of important covariates in those people during that week). This outcome statistic has several advantages. First, it accounts for the number of patients in the hospital each day. This is important because the number of hospital deaths will increase as the number of people in hospital increase. Second, it accounts for the severity of illness in each patient on each hospital day. This accounts for daily changes in risk of patient death, because calculation of the expected number of deaths per day was done using a multivariate survival model that included time‐dependent covariates. Therefore, each individual's predicted hazard of death (which was summed over the entire hospital to calculate the total expected number of deaths in hospital each day) took into account the latest values of these covariates. Previous analyses only accounted for risk of death at admission.
Expressing Physician Experience
The latent measure26 in all July Phenomenon studies is collective house‐staff physician experience. This is quantified by a surrogate date variable in which July 1the date that new house‐staff start their training in North Americarepresents minimal experience and June 30 represents maximal experience. We expressed collective physician experience on a scale from 0 (minimum experience) on July 1 to 1 (maximum experience) on June 30. A similar approach has been used previously13 and has advantages over the other methods used to capture collective house‐staff experience. In the stratified, incomplete approach,47, 911, 13, 1517 periods with inexperienced house‐staff (eg, July and August) are grouped together and compared to times with experienced house‐staff (eg, May and June), while ignoring all other data. The specification of cut‐points for this stratification is arbitrary and the method ignores large amounts of data. In the stratified, complete approach, periods with inexperienced house‐staff (eg, July and August) are grouped together and compared to all other times of the year.8, 12, 14, 1820, 22 This is potentially less biased because there are no lost data. However, the cut‐point for determining when house‐staff transition from inexperienced to experienced is arbitrary, and the model assumes that the transition is sudden. This is suboptimal because acquisition of experience is a gradual, constant process.
The pattern by which collective physician experience changes between July 1st and June 30th is unknown. We therefore expressed this evolution using five different patterns varying from a linear change to a natural logarithmic change (see Supporting Appendix B in the online version of this article).
Analysis
We first examined for autocorrelation in our outcome variable using Ljung‐Box statistics at lag 6 and 12 in PROC ARIMA (SAS 9.2, Cary, NC). If significant autocorrelation was absent in our data, linear regression modeling was used to associate the ratio of the observed to expected number of weekly deaths (the outcome variable) with the collective first year physician experience (the predictor variable). Time‐series methodology was to be used if significant autocorrelation was present.
In our baseline analysis, we included all hospitalizations together. In stratified analyses, we categorized hospitalizations by admission status (emergent vs elective) and admission service (medicine vs surgery).
RESULTS
Between April 15, 2004 and December 31, 2008, The Ottawa Hospital had a total of 152,017 inpatient admissions and 107,731 same day surgeries (an annual rate of 32,222 and 22,835, respectively; an average daily rate of 88 and 63, respectively) that met our study's inclusion criteria. These 259,748 encounters included 164,318 people. Table 1 provides an overall description of the study population.
| Characteristic | |
|---|---|
| |
| Patients/hospitalizations, n | 164,318/259,748 |
| Deaths in‐hospital, n (%) | 7,679 (3.0) |
| Length of admission in days, median (IQR) | 2 (16) |
| Male, n (%) | 124,848 (48.1) |
| Age at admission, median (IQR) | 60 (4674) |
| Admission type, n (%) | |
| Elective surgical | 136,406 (52.5) |
| Elective nonsurgical | 20,104 (7.7) |
| Emergent surgical | 32,046 (12.3) |
| Emergent nonsurgical | 71,192 (27.4) |
| Elixhauser score, median (IQR) | 0 (04) |
| LAPS at admission, median (IQR) | 0 (015) |
| At least one admission to intensive care unit, n (%) | 7,779 (3.0) |
| At least one alternative level of care episode, n (%) | 6,971 (2.7) |
| At least one PIMR procedure, n (%) | 47,288 (18.2) |
| First PIMR score,* median (IQR) | 2 (52) |
Weekly Deaths: Observed, Expected, and Ratio
Figure 1A presents the observed weekly number of deaths during the study period. There was an average of 31 deaths per week (range 1551). Some large fluctuations in the weekly number of deaths were seen; in 2007, for example, the number of observed deaths went from 21 in week 13 up to 46 in week 15. However, no obvious seasonal trends in the observed weekly number of deaths were seen (Figure 1A, heavy line) nor were trends between years obvious.

Figure 1B presents the expected weekly number of deaths during the study period. The expected weekly number of deaths averaged 29.6 (range 22.238.7). The expected weekly number of deaths was notably less variable than the observed number of deaths. However, important variations in the expected number of deaths were seen; for example, in 2005, the expected number of deaths increased from 24.1 in week 41 to 29.6 in week 44. Again, we saw no obvious seasonal trends in the expected weekly number of deaths (Figure 1B, heavy line).
Figure 1C illustrates the ratio of observed to the expected weekly number of deaths. The average observed to expected ratio slightly exceeded unity (1.05) and ranged from 0.488 (week 24, in 2008) to 1.821 (week 51, in 2008). We saw no obvious seasonal trends in the ratio of the observed to expected number of weekly deaths. In addition, obvious trends in this ratio were absent over the study period.
Association Between House‐Staff Experience and Death in Hospital
We found no evidence of autocorrelation in the ratio of observed to expected weekly number of deaths. The ratio of observed to expected number of hospital deaths was not significantly associated with house‐staff physician experience (Table 2). This conclusion did not change regardless of which house‐staff physician experience pattern was used in the linear model (Table 2). In addition, our analysis found no significant association between physician experience and patient mortality when analyses were stratified by admission service or admission status (Table 2).
| Patient Population | House‐Staff Experience Pattern (95% CI) | ||||
|---|---|---|---|---|---|
| Linear | Square | Square Root | Cubic | Natural Logarithm | |
| |||||
| All | 0.03 (0.11, 0.06) | 0.02 (0.10, 0.07) | 0.04 (0.15, 0.07) | 0.01 (0.10, 0.08) | 0.05 (0.16, 0.07) |
| Admitting service | |||||
| Medicine | 0.0004 (0.09, 0.10) | 0.01 (0.08, 0.10) | 0.01 (0.13, 0.11) | 0.02 (0.07, 0.11) | 0.03 (0.15, 0.09) |
| Surgery | 0.10 (0.30, 0.10) | 0.11 (0.30, 0.08) | 0.12 (0.37, 0.14) | 0.11 (0.31, 0.08) | 0.09 (0.35, 0.17) |
| Admission status | |||||
| Elective | 0.09 (0.53, 0.35) | 0.10 (0.51, 0.32) | 0.11 (0.66, 0.44) | 0.10 (0.53, 0.33) | 0.11 (0.68, 0.45) |
| Emergent | 0.02 (0.11, 0.07) | 0.01 (0.09, 0.08) | 0.03 (0.14, 0.08) | 0.003 (0.09, 0.09) | 0.04 (0.16, 0.08) |
DISCUSSION
It is natural to suspect that physician experience influences patient outcomes. The commonly discussed July Phenomenon explores changes in teaching‐hospital patient outcomes by time of the academic year. This serves as an ecological surrogate for the latent variable of overall house‐staff experience. Our study used a detailed outcomethe ratio of observed to the expected number of weekly hospital deathsthat adjusted for patient severity of illness. We also modeled collective physician experience using a broad range of patterns. We found no significant variation in mortality rates during the academic year; therefore, the risk of death in hospital does not vary by house‐staff experience at our hospital. This is no evidence of a July Phenomenon for mortality at our center.
We were not surprised that the arrival of inexperienced house‐staff did not significantly change patient mortality for several reasons. First year residents are but one group of treating physicians in a teaching hospital. They are surrounded by many other, more experienced physicians who also contribute to patient care and their outcomes. Given these other physicians, the influence that the relatively smaller number of first year residents have on patient outcomes will be minimized. In addition, the role that these more experienced physicians play in patient care will vary by the experience and ability of residents. The influence of new and inexperienced house‐staff in July will be blunted by an increased role played by staff‐people, fellows, and more experienced house‐staff at that time.
Our study was a methodologically rigorous examination of the July Phenomenon. We used a reliable outcome statisticthe ratio of observed to expected weekly number of hospital deathsthat was created with a validated, discriminative, and well‐calibrated model which predicted risk of death in hospital (Wong et al., Derivation and validation of a model to predict the daily risk of death in hospital, 2010, unpublished work). This statistic is inherently understandable and controlled for patient severity of illness. In addition, our study included a very broad and inclusive group of patients over five years at two hospitals.
Twenty‐three other studies have quantitatively sought a July Phenomenon for patient mortality (see Supporting Appendix A in the online version of this article). The studies contained a broad assortment of research methodologies, patient populations, and analytical methodologies. Nineteen of these studies (83%) found no evidence of a July Phenomenon for teaching‐hospital mortality. In contrast, two of these studies found notable adjusted odds ratios for death in hospital (1.41 and 1.34) in patients undergoing either general surgery13 or complex cardiovascular surgery,19 respectively. Blumberg22 also found an increased risk of death in surgical patients in July, but used indirect standardized mortality ratios as the outcome statistic and was based on only 139 cases at Maryland teaching hospitals in 1984. Only Jen et al.16 showed an increased risk of hospital death with new house‐staff in a broad patient population. However, this study was restricted to two arbitrarily chosen days (one before and one after house‐staff change‐over) and showed an increased risk of hospital death (adjusted OR 1.05, 95% CI 1.001.15) whose borderline statistical significance could have been driven by the large sample size of the study (n = 299,741).
Therefore, the vast majority of dataincluding those presented in our analysesshow that the risk of teaching‐hospital death does not significantly increase with the arrival of new house‐staff. This prompts the question as to why the July Phenomenon is commonly presented in popular media as a proven fact.2733 We believe this is likely because the concept of the July Phenomenon is understandable and has a rather morbid attraction to people, both inside and outside of the medical profession. Given the large amount of data refuting the true existence of a July Phenomenon for patient mortality (see Supporting Appendix A in the online version of this article), we believe that this term should only be used only as an example of an interesting idea that is refuted by a proper analysis of the data.
Several limitations of our study are notable. First, our analysis is limited to a single center, albeit with two hospitals. However, ours is one of the largest teaching centers in Canada with many new residents each year. Second, we only examined the association of physician experience on hospital mortality. While it is possible that physician experience significantly influences other patient outcomes, mortality is, obviously, an important and reliably tallied statistic that is used as the primary outcome in most July Phenomenon studies. Third, we excluded approximately a quarter of all hospitalizations from the study. These exclusions were necessary because the Escobar model does not apply to these people and can therefore not be used to predict their risk of death in hospital. However, the vast majority of excluded patients (those less than 15 years old, and women admitted for routine childbirth) have a very low risk of death (the former because they are almost exclusively newborns, and the latter because the risk of maternal death during childbirth is very low). Since these people will contribute very little to either the expected or observed number of deaths, their exclusion will do little to threaten the study's validity. The remaining patients who were transferred to or from other hospitals (n = 12,931) makes a small proportion of the total sampling frame (5% of admissions). Fourth, our study did not identify any significant association between house‐staff experience and patient mortality (Table 2). However, the confidence intervals around our estimates are wide enough, especially in some subgroups such as patients admitted electively, that important changes in patient mortality with house‐staff experience cannot be excluded. For example, whereas our study found that a decrease in the ratio of observed to expected number of deaths exceeding 30% is very unlikely, it is still possible that this decrease is up to 30% (the lower range of the confidence interval in Table 2). However, using this logic, it could also increase by up to 10% (Table 2). Finally, we did not directly measure individual physician experience. New residents can vary extensively in their individual experience and ability. Incorporating individual physician measures of experience and ability would more reliably let us measure the association of new residents with patient outcomes. Without this, we had to rely on an ecological measure of physician experiencenamely calendar date. Again, this method is an industry standard since all studies quantify physician experience ecologically by date (see Supporting Appendix A in the online version of this article).
In summary, our datasimilar to most studies on this topicshow that the risk of death in teaching hospitals does not change with the arrival of new house‐staff.
- ,,.The effects of scheduled intern rotation on the cost and quality of teaching hospital care.Eval Health Prof.1994;17:259–272.
- ,,,.Specialty differences in the “July Phenomenon” for Twin Cities teaching hospitals.Med Care.1993;31:73–83.
- ,,,.The relationship of house staff experience to the cost and quality of inpatient care.JAMA.1990;263:953–957.
- ,,,.Indirect costs for medical education. Is there a July phenomenon?Arch Intern Med.1989;149:765–768.
- ,,,,.The impact of accreditation council for graduate medical education duty hours, the July phenomenon, and hospital teaching status on stroke outcomes.J Stroke Cerebrovasc Dis.2009;18:232–238.
- ,.The killing season—Fact or fiction.BMJ1994;309:1690.
- ,,, et al.The July effect: Impact of the beginning of the academic cycle on cardiac surgical outcomes in a cohort of 70,616 patients.Ann Thorac Surg.2009;88:70–75.
- ,.Is there a July phenomenon? The effect of July admission on intensive care mortality and length of stay in teaching hospitals.J Gen Intern Med.2003;18:639–645.
- ,,,.Neonatal mortality among low birth weight infants during the initial months of the academic year.J Perinatol.2008;28:691–695.
- ,,,,.The “July Phenomenon” and the care of the severely injured patient: Fact or fiction?Surgery.2001;130:346–353.
- ,,, et al.The July effect and cardiac surgery: The effect of the beginning of the academic cycle on outcomes.Am J Surg.2008;196:720–725.
- ,,,.Mortality in Medicare patients undergoing surgery in July in teaching hospitals.Ann Surg.2009;249:871–876.
- ,,, et al.Seasonal variation in surgical outcomes as measured by the American College of Surgeons–National Surgical Quality Improvement Program (ACS‐NSQIP).Ann Surg.2007;246:456–465.
- ,,, et al.Mortality rate and length of stay of patients admitted to the intensive care unit in July.Crit Care Med.2004;32:1161–1165.
- ,,,,,.July—As good a time as any to be injured.J Trauma‐Injury Infect Crit Care.2009;67:1087–1090.
- ,,,,.Early in‐hospital mortality following trainee doctors' first day at work.PLoS ONE.2009;4.
- ,,.Effect of critical care medicine fellows on patient outcome in the intensive care unit.Acad Med.2006;81:S1–S4.
- ,,,,.The “July Phenomenon”: Is trauma the exception?J Am Coll Surg.2009;209:378–384.
- ,,.Impact of cardiothoracic resident turnover on mortality after cardiac surgery: A dynamic human factor.Ann Thorac Surg.2008;86:123–131.
- ,,.Is there a “July Phenomenon” in pediatric neurosurgery at teaching hospitals?J Neurosurg Pediatr.2006;105:169–176.
- ,,,,.Mortality and morbidity by month of birth of neonates admitted to an academic neonatal intensive care unit.Pediatrics.2008;122:E1048–E1052.
- .Measuring surgical quality in Maryland: A model.Health Aff.1988;7:62–78.
- ,,, et al.Complications and death at the start of the new academic year: Is there a July phenomenon?J Trauma‐Injury Infect Crit Care.2010;68(1):19–22.
- ,,,,,.Risk‐adjusting hospital inpatient mortality using automated inpatient, outpatient, and laboratory databases.Med Care.2008;46:232–239.
- ,,,.The Kaiser Permanente inpatient risk adjustment methodology was valid in an external patient population.J Clin Epidemiol.2010;63:798–803.
- .Introduction: The logic of latent variables.Latent Class Analysis.Newbury Park, CA:Sage;1987:5–10.
- July Effect. Wikipedia. Available at: http://en.wikipedia.org/wiki/July_effect. Accessed April 1,2011.
- Study proves “killing season” occurs as new doctors start work. September 23,2010. Herald Scotland. Available at: http://www.heraldscotland.com/news/health/study‐proves‐killing‐season‐occurs‐as‐new‐doctors‐start‐work‐1.921632. Accessed April 1, 2011.
- The “July effect”: Worst month for fatal hospital errors, study finds. June 3,2010. ABC News. Available at: http://abcnews.go.com/WN/WellnessNews/july‐month‐fatal‐hospital‐errors‐study‐finds/story?id=10819652. Accessed 1 April, 2011.
- “Deaths rise” with junior doctors. September 22,2010. BBC News. Available at: http://news.bbc.co.uk/2/hi/health/8269729.stm. Accessed April 1, 2011.
- .July: When not to go to the hospital. June 2,2010. Science News. Available at: http://www.sciencenews.org/view/generic/id/59865/title/July_When_not_to_go_to_the_hospital. Accessed April 1, 2011.
- July: A deadly time for hospitals. July 5,2010. National Public Radio. Available at: http://www.npr.org/templates/story/story.php?storyId=128321489. Accessed April 1, 2011.
- .Medical errors and patient safety: Beware the “July effect.” June 4,2010. Better Health. Available at: http://getbetterhealth.com/medical‐errors‐and‐patient‐safety‐beware‐of‐the‐july‐effect/2010.06.04. Accessed April 1, 2011.
- ,,.The effects of scheduled intern rotation on the cost and quality of teaching hospital care.Eval Health Prof.1994;17:259–272.
- ,,,.Specialty differences in the “July Phenomenon” for Twin Cities teaching hospitals.Med Care.1993;31:73–83.
- ,,,.The relationship of house staff experience to the cost and quality of inpatient care.JAMA.1990;263:953–957.
- ,,,.Indirect costs for medical education. Is there a July phenomenon?Arch Intern Med.1989;149:765–768.
- ,,,,.The impact of accreditation council for graduate medical education duty hours, the July phenomenon, and hospital teaching status on stroke outcomes.J Stroke Cerebrovasc Dis.2009;18:232–238.
- ,.The killing season—Fact or fiction.BMJ1994;309:1690.
- ,,, et al.The July effect: Impact of the beginning of the academic cycle on cardiac surgical outcomes in a cohort of 70,616 patients.Ann Thorac Surg.2009;88:70–75.
- ,.Is there a July phenomenon? The effect of July admission on intensive care mortality and length of stay in teaching hospitals.J Gen Intern Med.2003;18:639–645.
- ,,,.Neonatal mortality among low birth weight infants during the initial months of the academic year.J Perinatol.2008;28:691–695.
- ,,,,.The “July Phenomenon” and the care of the severely injured patient: Fact or fiction?Surgery.2001;130:346–353.
- ,,, et al.The July effect and cardiac surgery: The effect of the beginning of the academic cycle on outcomes.Am J Surg.2008;196:720–725.
- ,,,.Mortality in Medicare patients undergoing surgery in July in teaching hospitals.Ann Surg.2009;249:871–876.
- ,,, et al.Seasonal variation in surgical outcomes as measured by the American College of Surgeons–National Surgical Quality Improvement Program (ACS‐NSQIP).Ann Surg.2007;246:456–465.
- ,,, et al.Mortality rate and length of stay of patients admitted to the intensive care unit in July.Crit Care Med.2004;32:1161–1165.
- ,,,,,.July—As good a time as any to be injured.J Trauma‐Injury Infect Crit Care.2009;67:1087–1090.
- ,,,,.Early in‐hospital mortality following trainee doctors' first day at work.PLoS ONE.2009;4.
- ,,.Effect of critical care medicine fellows on patient outcome in the intensive care unit.Acad Med.2006;81:S1–S4.
- ,,,,.The “July Phenomenon”: Is trauma the exception?J Am Coll Surg.2009;209:378–384.
- ,,.Impact of cardiothoracic resident turnover on mortality after cardiac surgery: A dynamic human factor.Ann Thorac Surg.2008;86:123–131.
- ,,.Is there a “July Phenomenon” in pediatric neurosurgery at teaching hospitals?J Neurosurg Pediatr.2006;105:169–176.
- ,,,,.Mortality and morbidity by month of birth of neonates admitted to an academic neonatal intensive care unit.Pediatrics.2008;122:E1048–E1052.
- .Measuring surgical quality in Maryland: A model.Health Aff.1988;7:62–78.
- ,,, et al.Complications and death at the start of the new academic year: Is there a July phenomenon?J Trauma‐Injury Infect Crit Care.2010;68(1):19–22.
- ,,,,,.Risk‐adjusting hospital inpatient mortality using automated inpatient, outpatient, and laboratory databases.Med Care.2008;46:232–239.
- ,,,.The Kaiser Permanente inpatient risk adjustment methodology was valid in an external patient population.J Clin Epidemiol.2010;63:798–803.
- .Introduction: The logic of latent variables.Latent Class Analysis.Newbury Park, CA:Sage;1987:5–10.
- July Effect. Wikipedia. Available at: http://en.wikipedia.org/wiki/July_effect. Accessed April 1,2011.
- Study proves “killing season” occurs as new doctors start work. September 23,2010. Herald Scotland. Available at: http://www.heraldscotland.com/news/health/study‐proves‐killing‐season‐occurs‐as‐new‐doctors‐start‐work‐1.921632. Accessed April 1, 2011.
- The “July effect”: Worst month for fatal hospital errors, study finds. June 3,2010. ABC News. Available at: http://abcnews.go.com/WN/WellnessNews/july‐month‐fatal‐hospital‐errors‐study‐finds/story?id=10819652. Accessed 1 April, 2011.
- “Deaths rise” with junior doctors. September 22,2010. BBC News. Available at: http://news.bbc.co.uk/2/hi/health/8269729.stm. Accessed April 1, 2011.
- .July: When not to go to the hospital. June 2,2010. Science News. Available at: http://www.sciencenews.org/view/generic/id/59865/title/July_When_not_to_go_to_the_hospital. Accessed April 1, 2011.
- July: A deadly time for hospitals. July 5,2010. National Public Radio. Available at: http://www.npr.org/templates/story/story.php?storyId=128321489. Accessed April 1, 2011.
- .Medical errors and patient safety: Beware the “July effect.” June 4,2010. Better Health. Available at: http://getbetterhealth.com/medical‐errors‐and‐patient‐safety‐beware‐of‐the‐july‐effect/2010.06.04. Accessed April 1, 2011.
Copyright © 2011 Society of Hospital Medicine
Information Continuity on Outcomes
Hospitalists are common in North America.1, 2 Hospitalists have been associated with a range of beneficial outcomes including decreased length of stay.3, 4 A primary concern of the hospitalist model is its potential detrimental effect on continuity of care5 partly because patients are often not seen by their hospitalists after discharge.
Continuity of care6 is primarily composed of provider continuity (an ongoing relationship between a patient and a particular provider over time) and information continuity (availability of data from prior events for subsequent patient encounters).6 The association between continuity of care and patient outcomes has been quantified in many studies.720 However, the relationship of continuity and outcomes is especially relevant after discharge from the hospital since this is a time when patients have a high risk of poor patient outcomes21 and poor provider22 and information continuity.2325
The association between continuity and outcomes after hospital discharge has been directly quantified in 2 studies. One found that patients seen by a physician who treated them in the hospital had a significant adjusted relative risk reduction in 30‐day death or readmission of 5% and 3%, respectively.22 The other study found that patients discharged from a general medicine ward were less likely to be readmitted if they were seen by physicians who had access to their discharge summary.23 However, neither of these studies concurrently measured the influence of provider and information continuity on patient outcomes.
Determining whether and how continuity of care influences patient outcomes after hospital discharge is essential to improve health care in an evidence‐based fashion. In addition, the influence that hospital physician follow‐up has on patient outcomes can best be determined by measuring provider and information continuity in patients after hospital discharge. This study sought to measure the independent association of several provider and information continuity measures on death or urgent readmission after hospital discharge.
Methods
Study Design
This was a multicenter prospective cohort study of consecutive patients discharged to the community from the medical or surgical services of 11 Ontario hospitals (6 university‐affiliated hospitals and 5 community hospitals) in 5 cities after an elective or emergency hospitalization. Patients were invited to participate in the study if they were cognitively intact, had a telephone, and provided written informed consent. Patients were excluded if they were less than 18 years old, were discharged to nursing homes, or were not proficient in English and did not have someone to help communicate with study staff. Enrolled patients were excluded from the analysis if they had less than 2 physician visits prior to one of the study's outcomes or the end of patient observation (which was 6 months postdischarge). This final exclusion criterion was necessary since 2 continuity measures (including postdischarge physician continuity and postdischarge information continuity) were incalculable with less than 2 physician visits during follow‐up (Supporting information). The study was approved by the research ethics board of each participating hospital.
Data Collection
Prior to hospital discharge, patients were interviewed by study personnel to identify their baseline functional status, their living conditions, all physicians who regularly treated the patient prior to admission (including both family physicians and consultants), and chronic medical conditions. The latter were confirmed by a review of the patient's chart and hospital discharge summary, when available. Patients also provided principal contacts whom we could contact in the event patients could not be reached. The chart and discharge summary were also used to identify diagnoses in hospitalincluding complications (diagnoses arising in the hospital)and medications at discharge.
Patients or their designated contacts were telephoned 1, 3, and 6 months after hospital discharge to identify the date and the physician of all postdischarge physician visits. For each postdischarge physician visit, we determined whether the physician had access to a discharge summary for the index hospitalization. We also determined the availability of information from all previous postdischarge visits that the patient had with other physicians. The methods used to collect these data were previously detailed.26 Briefly, we used three complementary methods to elicit this information from each follow‐up physician. First, patients gave the physician a survey on which the physician listed all prior visits with other doctors for which they had information. If this survey was not returned, we faxed the survey to the physician. If the faxed survey was not returned, we telephoned the physician or their office staff and administered the survey over the telephone.
Continuity Measures
We measured components of both provider and information continuity. For the posthospitalization period, we measured provider continuity for physicians who had provided patient care during three distinct phases: the prehospital period; the hospital period; and the postdischarge period. Prehospital physicians were those classified by the patient as their regular physician(s) (defined as physiciansboth family physicians and consultantsthat they had seen in the past and were likely to see again in the future). Hospital provider continuity was divided into 2 components: hospital physician continuity (ie, the most responsible physician in the hospital); and hospital consultant continuity (ie, another physician who consulted on the patient during admission). Information continuity was divided into discharge summary continuity and postdischarge visit information continuity.
We quantified provider and information continuity using Breslau's Usual Provider of Continuity (UPC)27 measure. It is a widely used and validated continuity measure whose values are meaningful and interpretable.6 The UPC measures the proportion of visits with the physician of interest (for provider continuity) or the proportion of visits having the information of interest (for information continuity). The UPC was calculated as: $${\rm UPC} = {\rm n}_{\rm i} / {\rm N}$$
As the formulae in the supporting information suggest, all continuity measures were incalculable prior to the first postdischarge visit and all continuity measures changed value at each visit during patient observation. In addition, a particular physician visit could increase multiple continuity measures simultaneously. For example, a visit with a physician who was the hospital physician and who regularly treated the patient prior to the hospitalization would increase both hospital and prehospital provider continuity. If the patient had previously seen the physician after discharge, the visit would also increase postdischarge physician continuity.
Study Outcomes
Outcomes for the study included time to all‐cause death and time to all‐cause, urgent readmission. To be classified as urgent, readmissions could not be arranged when the patient was originally discharged from hospital or more than 4 weeks prior to the readmission. All hospital admissions meeting these criteria during the 6 month study period were labeled in this study as urgent readmissions even if they were unrelated to the index admission.
Principal contacts were called if we were unable to reach the patient to determine their outcomes. If the patient's vital status remained unclear, we contacted the Office of the Provincial Registrar to determine if and when the patient died during the 6 months after discharge from hospital.
Analysis
Outcome incidence densities and 95% confidence intervals [CIs] were calculated using PROC GENMOD in SAS to account for clustering of patients in hospitals. We used multivariate proportional hazards modeling to determine the independent association of provider and information continuity measures with time to death and time to urgent readmission. Patient observation started when patients were discharged from the hospital. Patient observation ended at the earliest of the following: death; urgent readmission to the hospital; end of follow‐up (which was 6 months after discharge from the hospital) or loss to follow‐up. Because hospital consultant continuity was very highly skewed (95.6% of patients had a value of 0; mean value of 0.016; skewness 6.9), it was not included in the primary regression models but was included in a sensitivity analysis.
To adjust for potential confounders in the association between continuity and the outcomes, our model included all factors that were independently associated with either the outcome or any continuity measure. Factors associated with death or urgent readmission were summarized using the LACE index.29 This index combines a patient's hospital length of stay, admission acuity, patient comorbidity (measured with the Charlson Score30 using updated disease category weights by Schneeweiss et al.),31 and emergency room utilization (measured as the number of visits in the 6 months prior to admission) into a single number ranging from 0 to 19. The LACE index was moderately discriminative and highly accurate at predicting 30‐day death or urgent readmission.29 In a separate study,28 we found that the following factors were independently associated with at least one of the continuity measures: patient age; patient sex; number of admissions in previous 6 months; number of regular treating physicians prior to admission; hospital service (medicine vs. surgery); and number of complications in the hospital (defined as new problems arising after admission to hospital). By including all factors that were independently associated with either the outcome or continuity, we controlled for all measured factors that could act as confounders in the association between continuity and outcomes. We accounted for the clustered study design by using conditional proportional hazards models that stratified by hospitals.32 Analytical details are given in the supporting information.
Results
Between October 2002 and July 2006, we enrolled 5035 patients from 11 hospitals (Figure 1). Of the 5035 patients, 274 (5.4%) had no follow up interview with study personnel. A total of 885 (17.6%) had fewer than 2 post discharge physician visits and were not included in the continuity analyses. This left 3876 patients for this analysis (77.0% of the original cohort), of which 3727 had complete follow up (96.1% of the study cohort). A total of 531 patients (10.6% of the original cohort) had incomplete follow‐up because: 342 (6.8%) were lost to follow‐up; 172 (3.4%) refused participation; and 24 (0.5%) were transferred into a nursing home during the first month of observation.
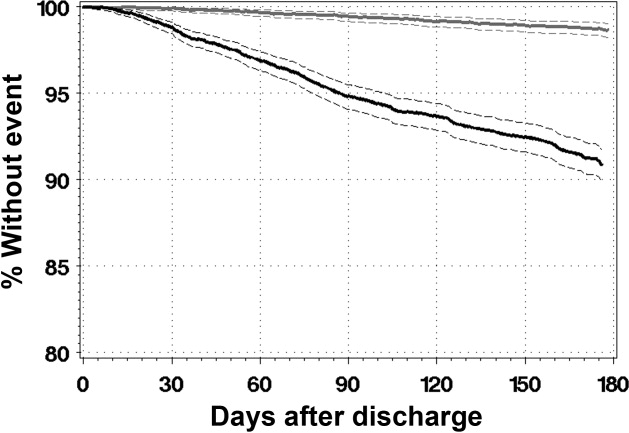
The 3876 study patients are described in Table 1. Overall, these people had a mean age of 62 and most commonly had no physical limitations. Almost a third of patients had been admitted to the hospital in the previous 6 months. A total of 7.6% of patients had no regular prehospital physician while 5.8% had more than one regular prehospital physician. Patients were evenly split between acute and elective admissions and 12% had a complication during their admission. They were discharged after a median of 4 days on a median of 4 medications.
| Factor | Value | Death or Urgent Readmission | All (n = 3876) | |
|---|---|---|---|---|
| No (n = 3491) | Yes (n = 385) | |||
| ||||
| Mean patient age, years (SD) | 61.59 16.16 | 67.70 15.53 | 62.19 16.20 | |
| Female (%) | 1838 (52.6) | 217 (56.4) | 2055 (53.0) | |
| Lives alone (%) | 791 (22.7) | 107 (27.8) | 898 (23.2) | |
| # activities of daily living requiring aids (%) | 0 | 3277 (93.9) | 354 (91.9) | 3631 (93.7) |
| 1 | 125 (3.6) | 20 (5.2) | 145 (3.7) | |
| >1 | 89 (2.5) | 11 (2.8) | 100 (2.8) | |
| # physicians who see patient regularly (%) | 0 | 241 (6.9) | 22 (5.7) | 263 (6.8) |
| 1 | 3060 (87.7) | 333 (86.5) | 3393 (87.5) | |
| 2 | 150 (4.3) | 21 (5.5) | 171 (4.4) | |
| >2 | 281 (8.0) | 31 (8.0) | 312 (8.0) | |
| # admissions in previous 6 months (%) | 0 | 2420 (69.3) | 222 (57.7) | 2642 (68.2) |
| 1 | 833 (23.9) | 103 (26.8) | 936 (24.1) | |
| >1 | 238 (6.8) | 60 (15.6) | 298 (7.7) | |
| Index hospitalization description | ||||
| Number of discharge medications (IQR) | 4 (2‐7) | 6 (3‐9) | 4 (2‐7) | |
| Admitted to medical service (%) | 1440 (41.2) | 231 (60.0) | 1671 (43.1) | |
| Acute diagnoses: | ||||
| CAD (%) | 238 (6.8) | 23 (6.0) | 261 (6.7) | |
| Neoplasm of unspecified nature (%) | 196 (5.6) | 35 (9.1) | 231 (6.0) | |
| Heart failure (%) | 127 (3.6) | 38 (9.9) | 165 (4.3) | |
| Acute procedures | ||||
| CABG (%) | 182 (5.2) | 14 (3.6) | 196 (5.1) | |
| Total knee arthoplasty (%) | 173 (5.0) | 10 (2.6) | 183 (4.7) | |
| Total hip arthroplasty (%) | 118 (3.4) | (0.5) | 120 (3.1) | |
| Complication during admission (%) | 403 (11.5) | 63 (16.4) | 466 (12.0) | |
| LACE index: mean (SD) | 8.0 (3.6) | 10.3 (3.8) | 8.2 (3.7) | |
| Length of stay in days: median (IQR) | 4 (2‐7) | 6 (3‐10) | 4 (2‐8) | |
| Acute/emergent admission (%) | 1851 (53.0) | 272 (70.6) | 2123 (54.8) | |
| Charlson score (%) | 0 | 2771 (79.4) | 241 (62.6) | 3012 (77.7) |
| 1 | 103 (3.0) | 17 (4.4) | 120 (3.1) | |
| 2 | 446 (12.8) | 86 (22.3) | 532 (13.7) | |
| >2 | 171 (4.9) | 41 (10.6) | 212 (5.5) | |
| Emergency room use (# visits/ year) (%) | 0 | 2342 (67.1) | 190 (49.4) | 2532 (65.3) |
| 1 | 761 (21.8) | 101 (26.2) | 862 (22.2) | |
| >1 | 388 (11.1) | 94 (24.4) | 482 (12.4) | |
Patients were observed in the study for a median of 175 days (interquartile range [IQR] 175‐178). During this time they had a median of 4 physician visits (IQR 3‐6). The first postdischarge physician visit occurred a median of 10 days (IQR 6‐18) after discharge from hospital.
Continuity Measures
Table 2 summarizes all continuity scores. Since continuity scores varied significantly over time,28 Table 2 provides continuity scores on the last day of patient observation. Preadmission provider, postdischarge provider, and discharge summary continuity all had similar values and distributions with median values ranging between 0.444 and 0.571. 1797 (46.4%) patients had a hospital physician provider continuity scorae of 0.
| Minimum | 25th Percentile | Median | 75th Percentile | Maximum | |
|---|---|---|---|---|---|
| Provider continuity | |||||
| A: Pre‐admission physician | 0 | 0.143 | 0.444 | 0.667 | 1.000 |
| B: Hospital physician | 0 | 0 | 0.143 | 0.400 | 1.000 |
| C: Post‐discharge physician | 0 | 0.333 | 0.571 | 0.750 | 1.000 |
| Information continuity | |||||
| D: Discharge summary | 0 | 0.095 | 0.500 | 0.800 | 1.000 |
| E: Post‐discharge information | 0 | 0 | 0.182 | 0.500 | 1.000 |
Study Outcomes
During a median of 175 days of observation, 45 patients died (event rate 2.6 events per 100 patient‐years observation [95% CI 2.0‐3.4]) and 340 patients were urgently readmitted (event rate 19.6 events per 100 patient‐years observation [95% CI 15.9‐24.3]). Figure 2 presents the survival curves for time to death and time to urgent readmission. The hazard of death was consistent through the observation period but the risk of urgent readmission decreased slightly after 90 days postdischarge.
Association Between Continuity and Outcomes
Table 3 summarizes the association between provider and information continuity with study outcomes. No continuity measure was associated with time to death by itself (Table 3, column A) or with the other continuity measures (Table 3, column B). Preadmission physician continuity was associated with a significantly decreased risk of urgent readmission. When the proportion of postdischarge visits with a prehospital physician increased by 10%, the adjusted risk of urgent readmission decreased by 6% (adjusted hazards ratio (adj‐HR)) of 0.94 (95% CI, 0.91‐0.98). None of the other continuity measuresincluding hospital physicianwere significantly associated with urgent readmission either by themselves (Table 3, column A) or after adjusting for other continuity measures (Table 3, column B).
| Outcome | ||||||||
|---|---|---|---|---|---|---|---|---|
| Death (95% CI) | Urgent Readmission (95% CI) | |||||||
| A: Adjusted for Other Confounders Only | B: Adjusted for Other Confounders and Continuity Measures | A: Adjusted for Other Confounders Only | B: Adjusted for Other Confounders and Continuity Measures | |||||
| ||||||||
| Provider continuity | ||||||||
| A: Pre‐admission physician | 1.03 | (0.95, 1.12) | 1.06 | (0.95, 1.18) | 0.95 | (0.92, 0.98) | 0.94 | (0.91, 0.98) |
| B: Hospital physician | 0.87 | (0.74, 1.02) | 0.86 | (0.70, 1.03) | 0.98 | (0.94, 1.02) | 0.97 | (0.92, 1.01) |
| C: Post‐discharge physician | 0.97 | (0.89, 1.06) | 0.93 | (0.84, 1.04) | 0.98 | (0.95, 1.01) | 0.98 | (0.94, 1.02) |
| Information continuity | ||||||||
| D: Discharge Summary | 0.96 | (0.89, 1.04) | 0.94 | (0.87, 1.03) | 1.01 | (0.98, 1.04) | 1.02 | (0.99, 1.05) |
| E: Post‐discharge information | 1.01 | (0.94, 1.08) | 1.03 | (0.95, 1.11) | 1.00 | (0.97, 1.03) | 1.03 | (0.95, 1.11) |
| Other confounders | ||||||||
| Patient age in decades* | 1.43 | (1.13, 1.82) | 1.18 | (1.10, 1.28) | ||||
| Female | 1.50 | (0.81, 2.77) | 1.16 | (0.94, 1.44) | ||||
| # physicians who see patient regularly | ||||||||
| 1 | 1.46 | (0.92, 2.34) | ||||||
| 2 | 2.17 | (1.11, 4.26) | ||||||
| >2 | 3.71 | (1.55, 8.88) | ||||||
| Complications during admission | ||||||||
| 1 | 1.38 | (0.61, 3.10) | 0.81 | (0.55, 1.17) | ||||
| >1 | 1.01 | (0.28, 3.58) | 0.91 | (0.56, 1.48) | ||||
| # admissions in previous 6 months | ||||||||
| 1 | 1.27 | (0.59, 2.70) | 1.34 | (1.02, 1.76) | ||||
| >1 | 1.42 | (0.55, 3.67) | 1.78 | (1.26, 2.51) | ||||
| LACE index* | 1.16 | (1.06, 1.26) | 1.10 | (1.07, 1.14) | ||||
Increased patient age and increased LACE index score were both strongly associated with an increased risk of death (adj‐HR 1.43 [1.13‐1.82] and 1.16 [1.06‐1.26], respectively) and urgent readmission (adj‐HR 1.18 [1.10‐1.28] and 1.10 [1.07‐1.14], respectively). Hospitalization in the 6 months prior to admission significantly increased the risk of urgent readmission but not death. The risk of urgent readmission increased significantly as the number of regular prehospital physicians increased.
Sensitivity Analyses
Our study conclusions did not change in the sensitivity analyses. The number of postdischarge physician visits (expressed as a time‐dependent covariate) was not associated with either death or with urgent readmission and preadmission physician continuity remained significantly associated with time to urgent readmission (supporting information). Adding consultant continuity to the model also did not change our results (supporting information). In‐hospital consultant continuity was associated with an increased risk of urgent readmission (adj‐HR 1.10, 95% CI, 1.01‐1.20). The association between pre‐admission physician continuity and time to urgent readmission did not interact significantly with patient age, LACE index score, or number of previous admissions.
Discussion
This large, prospective cohort study measured the independent association of several provider and information continuity measures with important outcomes in patients discharged from hospital. After adjusting for potential confounders, we found that increased continuity with physicians who regularly cared for the patient prior to the admission was significantly and independently associated with a decreased risk of urgent readmission. Our data suggest that continuity with the hospital physician did not independently influence the risk of patient death or urgent readmission after discharge.
Although hospital physician continuity did not significantly change patient outcomes, we found that follow‐up with a physician who regularly treated the patient prior to their admission was associated with a significantly decreased risk of urgent readmission. This could reflect the important role that a patient's regular physician plays in their health care. Other studies have shown a positive association between continuity with a regular physician and improved outcomes including decreased emergency room utilization7, 8 and decreased hospitalization.10, 11
We were somewhat disappointed that information continuity was not independently associated with improved patient outcomes. Information continuity is likely more amenable to modification than is provider continuity. Of course, our study findings do not mean that information continuity does not improve patient outcomes, as in other studies.23, 33 Instead, our results could reflect that we solely measured the availability of information to physicians. Future studies that measure the quality, relevance, and actual utilization of patient information will be better able to discern the influence of information continuity on patient outcomes.
We believe that our study was methodologically strong and unique. We captured both provider and information continuity in a large group of representative patients using a broad range of measures that captured continuity's diverse components including both provider and information continuity. The continuity measures were expressed and properly analyzed as time‐dependent variables in a multivariate model.34 Our analysis controlled for important potential confounders. Our follow‐up and data collection was rigorous with 96.1% of our study group having complete follow‐up. Finally, the analysis used multiple imputation to appropriately handle missing data in the one incomplete variable (post‐discharge information continuity).3537
Several limitations of our study should be kept in mind. We are uncertain how our results might generalize to patients discharged from obstetrical or psychiatric services or people in other health systems. Our analysis had to exclude patients with less than two physician visits after discharge since this was the minimum required to calculate postdischarge physician and information continuity. Data collection for postdischarge information continuity was incomplete with data missing for 19.0% of all 15 401 visits in the original cohort.38 However, a response rate of 81.0% is very good39 when compared to other survey‐based studies40 and we accounted for the missing data using multiple imputation methods. The primary outcomes of our studytime to death or urgent readmissionmay be relatively insensitive to modification of quality of care, which is presumably improved by increased continuity.41 For example, Clarke found that the majority of readmissions in all patient groups were unavoidable with 94% of medical readmissions 1 month postdischarge judged to be unavoidable.42 Future studies regarding the effects of continuity could focus on its association with other outcomes that are more reflective of quality of care such as the risk of adverse events or medical error.21 Such outcomes would presumably be more sensitive to improved quality of care from increased continuity.
We believe that our study's major limitation was its inability to establish a causal association between continuity and patient outcomes. Our finding that increased consultant continuity was associated with an increased risk of poor outcomes highlights this concern. Presumably, patient follow‐up with a hospital consultant indicates a disease status with a high risk of bad patient outcomesa risk that is not entirely accounted for by the covariates used in this study. If we accept that unresolved confounding explains this association, the same could also apply to the association between preadmission physician continuity and improved outcomes. Perhaps patients who are doing well after discharge from hospital are able to return to their regular physician. Our analysis would therefore identify an association between increased preadmission physician continuity and improved patient outcomes. Analyses could also incorporate more discriminative measures of severity of hospital illness, such as those developed by Escobar et al.43 Since patients may experience health events after their discharge from hospital that could influence outcomes, recording these and expressing them in the study model as time‐dependent covariates will be important. Finally, similar to the classic study by Wasson et al.44 in 1984, a proper randomized trial that measures the effect of a continuity‐building intervention on both continuity of care and patient outcomes would help determine how continuity influences outcomes.
In conclusion, after discharge from hospital, increased continuity with physicians who routinely care for the patient is significantly and independently associated with a decreased risk of urgent readmission. Continuity with the hospital physician after discharge did not independently influence the risk of patient death or urgent readmission in our study. Further research is required to determine the causal association between preadmission physician continuity and improved outcomes. Until that time, clinicians should strive to optimize continuity with physicians their patients have seen prior to the hospitalization.
- Society of Hospital Medicine.2009.Ref Type: Internet Communication.
- ,,,.The status of hospital medicine groups in the United States.J Hosp Med.2006;1:75–80.
- ,.The hospitalist movement 5 years later. [see comment].JAMA.2002;287:487–494. [Review]
- ,,,.Hospitalists and the practice of inpatient medicine: results of a survey of the National Association of Inpatient Physicians. [see comment].Ann Intern Med.1999;130:343–349.
- ,,,.Primary care physician attitudes regarding communication with hospitalists.Am J Med.2001;111:15S–20S.
- ,,.Defusing the confusion: concepts and measures of continuity of healthcare.Ottawa,Canadian Health Services Research Foundation. Ref Type: Report.2002;1–50.
- ,,,,.Association between infant continuity of care and pediatric emergency department utilization.Pediatrics.2004;113:738–741.
- ,,,,.Is greater continuity of care associated with less emergency department utilization?Pediatrics.1999;103:738–742.
- ,,,,.Association of lower continuity of care with greater risk of emergency department use and hospitalization in children.Pediatrics.2001;107:524–529.
- ,,The role of provider continuity in preventing hospitalizations.Arch Fam Med.1998;7:352–357.
- ,.The importance of continuity of care in the likelihood of future hospitalization: is site of care equivalent to a primary clinician?Am J Public Health.1998;88:1539–1541.
- ,,,.Exploration of the relationship between continuity, trust in regular doctors and patient satisfaction with consultations with family doctors.Scand J Prim Health Care.2003;21:27–32.
- ,,,,.Longitudinal continuity of care is associated with high patient satisfaction with physical therapy.Phys Ther.2005;85:1046–1052.
- ,,,,.Provider continuity and outcomes of care for persons with schizophrenia.Ment Health Serv Res.2000;V2:201–211.
- ,,,,.Continuity of care is associated with well‐coordinated care.Ambul Pediatr.2003;3:82–86.
- ,,.The impact of insurance type and forced discontinuity on the delivery of primary care. [see comments.].J Fam Pract.1997;45:129–135.
- .Measuring attributes of primary care: development of a new instrument.J Fam Pract.1997;45:64–74.
- .Continuity of care during pregnancy: the effect of provider continuity on outcome.J Fam Pract.1985;21:375–380.
- ,,,,,.Physician‐patient relationship and medication compliance: a primary care investigation.Ann Fam Med.2004;2:455–461.
- ,,,.Continuity of care and cardiovascular risk factor management: does care by a single clinician add to informational continuity provided by electronic medical records?Am J Manag Care.2005;11:689–696.
- ,,,,.The incidence and severity of adverse events affecting patients after discharge from the hospital.Ann Intern Med.2003;138:161–167.
- ,,,.Continuity of care and patient outcomes after hospital discharge.J Gen lntern Med.2004;19:624–645.
- ,,,.Effect of discharge summary availability during post‐discharge visits on hospital readmission.J Gen Intern Med.2002;17:186–192.
- ,,, et al.Association of communication between hospital‐based physicians and primary care providers with patient outcomes.[see comment].J Gen Intern Med2009;24(3):381–386.
- ,,,,,.Deficits in communication and information transfer between hospital‐based and primary care physicians: implications for patient safety and continuity of care.JAMA.2007;297:831–841.
- ,,, et al.Information exchange among physicians caring for the same patient in the community.Can Med Assoc J.2008;179:1013–1018.
- ,.Continuity of care in a university‐based practice.J Med Educ.1975;965–969.
- ,,, et al.Provider and information continuity after discharge from hospital: a prospective cohort study.2009. Ref Type: Unpublished Work.
- ,,, et al.Derivation and validation of the LACE index to predict early death or unplanned readmission after discharge from hospital to the community.CMAJ. (In press)
- ,,,.A new method of classifying prognostic comorbidity in longitudinal studies: development and validation.J Chronic Dis.1987;40:373–383.
- ,,,.Improved comorbidity adjustment for predicting mortality in Medicare populations.Health Serv Res.2003;38(4):1103–1120.
- ,.Modelling clustered survival data from multicentre clinical trials.Stat Med.2004;23:369–388.
- ,,,.Prevalence of information gaps in the emergency department and the effect on patient outcomes.CMAJ.2003;169:1023–1028.
- ,,,.Time‐dependent bias due to improper analytical methodology is common in prominent medical journals.J Clin Epidemiol.2004;57:672–682.
- .What do we do with missing data? Some options for analysis of incomplete data.Annu Rev Public Health.2004;25:99–117.
- ,,,.Survival estimates of a prognostic classification depended more on year of treatment than on imputation of missing values.J Clin Epidemiol.2006;59:246–253. [Review]
- .Bias arising from missing data in predictive models.[see comment].J Clin Epidemiol.2006;59:1115–1123.
- ,,, et al.Information exchange among physicians caring for the same patient in the community.CMAJ.2008;179:1013–1018.
- .Survey Research Methods.2nd ed.,Beverly Hills:Sage;1993.
- ,,.Response rates to mail surveys published in medical journals.J Clin Epidemiol.1997;50:1129–1136.
- .Readmission of patients to hospital: still ill defined and poorly understood.Int J Qual Health Care.2001;13:177–179.
- .Are readmissions avoidable?Br Med J.1990;301:1136–1138.
- ,,,,,.Risk‐adjusting hospital inpatient mortality using automated inpatient, outpatient, and laboratory databases.Med Care.2008;46:232–239.
- ,,, et al.Continuity of outpatient medical care in elderly men. A randomized trial.JAMA.1984;252:2413–2417.
Hospitalists are common in North America.1, 2 Hospitalists have been associated with a range of beneficial outcomes including decreased length of stay.3, 4 A primary concern of the hospitalist model is its potential detrimental effect on continuity of care5 partly because patients are often not seen by their hospitalists after discharge.
Continuity of care6 is primarily composed of provider continuity (an ongoing relationship between a patient and a particular provider over time) and information continuity (availability of data from prior events for subsequent patient encounters).6 The association between continuity of care and patient outcomes has been quantified in many studies.720 However, the relationship of continuity and outcomes is especially relevant after discharge from the hospital since this is a time when patients have a high risk of poor patient outcomes21 and poor provider22 and information continuity.2325
The association between continuity and outcomes after hospital discharge has been directly quantified in 2 studies. One found that patients seen by a physician who treated them in the hospital had a significant adjusted relative risk reduction in 30‐day death or readmission of 5% and 3%, respectively.22 The other study found that patients discharged from a general medicine ward were less likely to be readmitted if they were seen by physicians who had access to their discharge summary.23 However, neither of these studies concurrently measured the influence of provider and information continuity on patient outcomes.
Determining whether and how continuity of care influences patient outcomes after hospital discharge is essential to improve health care in an evidence‐based fashion. In addition, the influence that hospital physician follow‐up has on patient outcomes can best be determined by measuring provider and information continuity in patients after hospital discharge. This study sought to measure the independent association of several provider and information continuity measures on death or urgent readmission after hospital discharge.
Methods
Study Design
This was a multicenter prospective cohort study of consecutive patients discharged to the community from the medical or surgical services of 11 Ontario hospitals (6 university‐affiliated hospitals and 5 community hospitals) in 5 cities after an elective or emergency hospitalization. Patients were invited to participate in the study if they were cognitively intact, had a telephone, and provided written informed consent. Patients were excluded if they were less than 18 years old, were discharged to nursing homes, or were not proficient in English and did not have someone to help communicate with study staff. Enrolled patients were excluded from the analysis if they had less than 2 physician visits prior to one of the study's outcomes or the end of patient observation (which was 6 months postdischarge). This final exclusion criterion was necessary since 2 continuity measures (including postdischarge physician continuity and postdischarge information continuity) were incalculable with less than 2 physician visits during follow‐up (Supporting information). The study was approved by the research ethics board of each participating hospital.
Data Collection
Prior to hospital discharge, patients were interviewed by study personnel to identify their baseline functional status, their living conditions, all physicians who regularly treated the patient prior to admission (including both family physicians and consultants), and chronic medical conditions. The latter were confirmed by a review of the patient's chart and hospital discharge summary, when available. Patients also provided principal contacts whom we could contact in the event patients could not be reached. The chart and discharge summary were also used to identify diagnoses in hospitalincluding complications (diagnoses arising in the hospital)and medications at discharge.
Patients or their designated contacts were telephoned 1, 3, and 6 months after hospital discharge to identify the date and the physician of all postdischarge physician visits. For each postdischarge physician visit, we determined whether the physician had access to a discharge summary for the index hospitalization. We also determined the availability of information from all previous postdischarge visits that the patient had with other physicians. The methods used to collect these data were previously detailed.26 Briefly, we used three complementary methods to elicit this information from each follow‐up physician. First, patients gave the physician a survey on which the physician listed all prior visits with other doctors for which they had information. If this survey was not returned, we faxed the survey to the physician. If the faxed survey was not returned, we telephoned the physician or their office staff and administered the survey over the telephone.
Continuity Measures
We measured components of both provider and information continuity. For the posthospitalization period, we measured provider continuity for physicians who had provided patient care during three distinct phases: the prehospital period; the hospital period; and the postdischarge period. Prehospital physicians were those classified by the patient as their regular physician(s) (defined as physiciansboth family physicians and consultantsthat they had seen in the past and were likely to see again in the future). Hospital provider continuity was divided into 2 components: hospital physician continuity (ie, the most responsible physician in the hospital); and hospital consultant continuity (ie, another physician who consulted on the patient during admission). Information continuity was divided into discharge summary continuity and postdischarge visit information continuity.
We quantified provider and information continuity using Breslau's Usual Provider of Continuity (UPC)27 measure. It is a widely used and validated continuity measure whose values are meaningful and interpretable.6 The UPC measures the proportion of visits with the physician of interest (for provider continuity) or the proportion of visits having the information of interest (for information continuity). The UPC was calculated as: $${\rm UPC} = {\rm n}_{\rm i} / {\rm N}$$
As the formulae in the supporting information suggest, all continuity measures were incalculable prior to the first postdischarge visit and all continuity measures changed value at each visit during patient observation. In addition, a particular physician visit could increase multiple continuity measures simultaneously. For example, a visit with a physician who was the hospital physician and who regularly treated the patient prior to the hospitalization would increase both hospital and prehospital provider continuity. If the patient had previously seen the physician after discharge, the visit would also increase postdischarge physician continuity.
Study Outcomes
Outcomes for the study included time to all‐cause death and time to all‐cause, urgent readmission. To be classified as urgent, readmissions could not be arranged when the patient was originally discharged from hospital or more than 4 weeks prior to the readmission. All hospital admissions meeting these criteria during the 6 month study period were labeled in this study as urgent readmissions even if they were unrelated to the index admission.
Principal contacts were called if we were unable to reach the patient to determine their outcomes. If the patient's vital status remained unclear, we contacted the Office of the Provincial Registrar to determine if and when the patient died during the 6 months after discharge from hospital.
Analysis
Outcome incidence densities and 95% confidence intervals [CIs] were calculated using PROC GENMOD in SAS to account for clustering of patients in hospitals. We used multivariate proportional hazards modeling to determine the independent association of provider and information continuity measures with time to death and time to urgent readmission. Patient observation started when patients were discharged from the hospital. Patient observation ended at the earliest of the following: death; urgent readmission to the hospital; end of follow‐up (which was 6 months after discharge from the hospital) or loss to follow‐up. Because hospital consultant continuity was very highly skewed (95.6% of patients had a value of 0; mean value of 0.016; skewness 6.9), it was not included in the primary regression models but was included in a sensitivity analysis.
To adjust for potential confounders in the association between continuity and the outcomes, our model included all factors that were independently associated with either the outcome or any continuity measure. Factors associated with death or urgent readmission were summarized using the LACE index.29 This index combines a patient's hospital length of stay, admission acuity, patient comorbidity (measured with the Charlson Score30 using updated disease category weights by Schneeweiss et al.),31 and emergency room utilization (measured as the number of visits in the 6 months prior to admission) into a single number ranging from 0 to 19. The LACE index was moderately discriminative and highly accurate at predicting 30‐day death or urgent readmission.29 In a separate study,28 we found that the following factors were independently associated with at least one of the continuity measures: patient age; patient sex; number of admissions in previous 6 months; number of regular treating physicians prior to admission; hospital service (medicine vs. surgery); and number of complications in the hospital (defined as new problems arising after admission to hospital). By including all factors that were independently associated with either the outcome or continuity, we controlled for all measured factors that could act as confounders in the association between continuity and outcomes. We accounted for the clustered study design by using conditional proportional hazards models that stratified by hospitals.32 Analytical details are given in the supporting information.
Results
Between October 2002 and July 2006, we enrolled 5035 patients from 11 hospitals (Figure 1). Of the 5035 patients, 274 (5.4%) had no follow up interview with study personnel. A total of 885 (17.6%) had fewer than 2 post discharge physician visits and were not included in the continuity analyses. This left 3876 patients for this analysis (77.0% of the original cohort), of which 3727 had complete follow up (96.1% of the study cohort). A total of 531 patients (10.6% of the original cohort) had incomplete follow‐up because: 342 (6.8%) were lost to follow‐up; 172 (3.4%) refused participation; and 24 (0.5%) were transferred into a nursing home during the first month of observation.


The 3876 study patients are described in Table 1. Overall, these people had a mean age of 62 and most commonly had no physical limitations. Almost a third of patients had been admitted to the hospital in the previous 6 months. A total of 7.6% of patients had no regular prehospital physician while 5.8% had more than one regular prehospital physician. Patients were evenly split between acute and elective admissions and 12% had a complication during their admission. They were discharged after a median of 4 days on a median of 4 medications.
| Factor | Value | Death or Urgent Readmission | All (n = 3876) | |
|---|---|---|---|---|
| No (n = 3491) | Yes (n = 385) | |||
| ||||
| Mean patient age, years (SD) | 61.59 16.16 | 67.70 15.53 | 62.19 16.20 | |
| Female (%) | 1838 (52.6) | 217 (56.4) | 2055 (53.0) | |
| Lives alone (%) | 791 (22.7) | 107 (27.8) | 898 (23.2) | |
| # activities of daily living requiring aids (%) | 0 | 3277 (93.9) | 354 (91.9) | 3631 (93.7) |
| 1 | 125 (3.6) | 20 (5.2) | 145 (3.7) | |
| >1 | 89 (2.5) | 11 (2.8) | 100 (2.8) | |
| # physicians who see patient regularly (%) | 0 | 241 (6.9) | 22 (5.7) | 263 (6.8) |
| 1 | 3060 (87.7) | 333 (86.5) | 3393 (87.5) | |
| 2 | 150 (4.3) | 21 (5.5) | 171 (4.4) | |
| >2 | 281 (8.0) | 31 (8.0) | 312 (8.0) | |
| # admissions in previous 6 months (%) | 0 | 2420 (69.3) | 222 (57.7) | 2642 (68.2) |
| 1 | 833 (23.9) | 103 (26.8) | 936 (24.1) | |
| >1 | 238 (6.8) | 60 (15.6) | 298 (7.7) | |
| Index hospitalization description | ||||
| Number of discharge medications (IQR) | 4 (2‐7) | 6 (3‐9) | 4 (2‐7) | |
| Admitted to medical service (%) | 1440 (41.2) | 231 (60.0) | 1671 (43.1) | |
| Acute diagnoses: | ||||
| CAD (%) | 238 (6.8) | 23 (6.0) | 261 (6.7) | |
| Neoplasm of unspecified nature (%) | 196 (5.6) | 35 (9.1) | 231 (6.0) | |
| Heart failure (%) | 127 (3.6) | 38 (9.9) | 165 (4.3) | |
| Acute procedures | ||||
| CABG (%) | 182 (5.2) | 14 (3.6) | 196 (5.1) | |
| Total knee arthoplasty (%) | 173 (5.0) | 10 (2.6) | 183 (4.7) | |
| Total hip arthroplasty (%) | 118 (3.4) | (0.5) | 120 (3.1) | |
| Complication during admission (%) | 403 (11.5) | 63 (16.4) | 466 (12.0) | |
| LACE index: mean (SD) | 8.0 (3.6) | 10.3 (3.8) | 8.2 (3.7) | |
| Length of stay in days: median (IQR) | 4 (2‐7) | 6 (3‐10) | 4 (2‐8) | |
| Acute/emergent admission (%) | 1851 (53.0) | 272 (70.6) | 2123 (54.8) | |
| Charlson score (%) | 0 | 2771 (79.4) | 241 (62.6) | 3012 (77.7) |
| 1 | 103 (3.0) | 17 (4.4) | 120 (3.1) | |
| 2 | 446 (12.8) | 86 (22.3) | 532 (13.7) | |
| >2 | 171 (4.9) | 41 (10.6) | 212 (5.5) | |
| Emergency room use (# visits/ year) (%) | 0 | 2342 (67.1) | 190 (49.4) | 2532 (65.3) |
| 1 | 761 (21.8) | 101 (26.2) | 862 (22.2) | |
| >1 | 388 (11.1) | 94 (24.4) | 482 (12.4) | |
Patients were observed in the study for a median of 175 days (interquartile range [IQR] 175‐178). During this time they had a median of 4 physician visits (IQR 3‐6). The first postdischarge physician visit occurred a median of 10 days (IQR 6‐18) after discharge from hospital.
Continuity Measures
Table 2 summarizes all continuity scores. Since continuity scores varied significantly over time,28 Table 2 provides continuity scores on the last day of patient observation. Preadmission provider, postdischarge provider, and discharge summary continuity all had similar values and distributions with median values ranging between 0.444 and 0.571. 1797 (46.4%) patients had a hospital physician provider continuity scorae of 0.
| Minimum | 25th Percentile | Median | 75th Percentile | Maximum | |
|---|---|---|---|---|---|
| Provider continuity | |||||
| A: Pre‐admission physician | 0 | 0.143 | 0.444 | 0.667 | 1.000 |
| B: Hospital physician | 0 | 0 | 0.143 | 0.400 | 1.000 |
| C: Post‐discharge physician | 0 | 0.333 | 0.571 | 0.750 | 1.000 |
| Information continuity | |||||
| D: Discharge summary | 0 | 0.095 | 0.500 | 0.800 | 1.000 |
| E: Post‐discharge information | 0 | 0 | 0.182 | 0.500 | 1.000 |
Study Outcomes
During a median of 175 days of observation, 45 patients died (event rate 2.6 events per 100 patient‐years observation [95% CI 2.0‐3.4]) and 340 patients were urgently readmitted (event rate 19.6 events per 100 patient‐years observation [95% CI 15.9‐24.3]). Figure 2 presents the survival curves for time to death and time to urgent readmission. The hazard of death was consistent through the observation period but the risk of urgent readmission decreased slightly after 90 days postdischarge.
Association Between Continuity and Outcomes
Table 3 summarizes the association between provider and information continuity with study outcomes. No continuity measure was associated with time to death by itself (Table 3, column A) or with the other continuity measures (Table 3, column B). Preadmission physician continuity was associated with a significantly decreased risk of urgent readmission. When the proportion of postdischarge visits with a prehospital physician increased by 10%, the adjusted risk of urgent readmission decreased by 6% (adjusted hazards ratio (adj‐HR)) of 0.94 (95% CI, 0.91‐0.98). None of the other continuity measuresincluding hospital physicianwere significantly associated with urgent readmission either by themselves (Table 3, column A) or after adjusting for other continuity measures (Table 3, column B).
| Outcome | ||||||||
|---|---|---|---|---|---|---|---|---|
| Death (95% CI) | Urgent Readmission (95% CI) | |||||||
| A: Adjusted for Other Confounders Only | B: Adjusted for Other Confounders and Continuity Measures | A: Adjusted for Other Confounders Only | B: Adjusted for Other Confounders and Continuity Measures | |||||
| ||||||||
| Provider continuity | ||||||||
| A: Pre‐admission physician | 1.03 | (0.95, 1.12) | 1.06 | (0.95, 1.18) | 0.95 | (0.92, 0.98) | 0.94 | (0.91, 0.98) |
| B: Hospital physician | 0.87 | (0.74, 1.02) | 0.86 | (0.70, 1.03) | 0.98 | (0.94, 1.02) | 0.97 | (0.92, 1.01) |
| C: Post‐discharge physician | 0.97 | (0.89, 1.06) | 0.93 | (0.84, 1.04) | 0.98 | (0.95, 1.01) | 0.98 | (0.94, 1.02) |
| Information continuity | ||||||||
| D: Discharge Summary | 0.96 | (0.89, 1.04) | 0.94 | (0.87, 1.03) | 1.01 | (0.98, 1.04) | 1.02 | (0.99, 1.05) |
| E: Post‐discharge information | 1.01 | (0.94, 1.08) | 1.03 | (0.95, 1.11) | 1.00 | (0.97, 1.03) | 1.03 | (0.95, 1.11) |
| Other confounders | ||||||||
| Patient age in decades* | 1.43 | (1.13, 1.82) | 1.18 | (1.10, 1.28) | ||||
| Female | 1.50 | (0.81, 2.77) | 1.16 | (0.94, 1.44) | ||||
| # physicians who see patient regularly | ||||||||
| 1 | 1.46 | (0.92, 2.34) | ||||||
| 2 | 2.17 | (1.11, 4.26) | ||||||
| >2 | 3.71 | (1.55, 8.88) | ||||||
| Complications during admission | ||||||||
| 1 | 1.38 | (0.61, 3.10) | 0.81 | (0.55, 1.17) | ||||
| >1 | 1.01 | (0.28, 3.58) | 0.91 | (0.56, 1.48) | ||||
| # admissions in previous 6 months | ||||||||
| 1 | 1.27 | (0.59, 2.70) | 1.34 | (1.02, 1.76) | ||||
| >1 | 1.42 | (0.55, 3.67) | 1.78 | (1.26, 2.51) | ||||
| LACE index* | 1.16 | (1.06, 1.26) | 1.10 | (1.07, 1.14) | ||||
Increased patient age and increased LACE index score were both strongly associated with an increased risk of death (adj‐HR 1.43 [1.13‐1.82] and 1.16 [1.06‐1.26], respectively) and urgent readmission (adj‐HR 1.18 [1.10‐1.28] and 1.10 [1.07‐1.14], respectively). Hospitalization in the 6 months prior to admission significantly increased the risk of urgent readmission but not death. The risk of urgent readmission increased significantly as the number of regular prehospital physicians increased.
Sensitivity Analyses
Our study conclusions did not change in the sensitivity analyses. The number of postdischarge physician visits (expressed as a time‐dependent covariate) was not associated with either death or with urgent readmission and preadmission physician continuity remained significantly associated with time to urgent readmission (supporting information). Adding consultant continuity to the model also did not change our results (supporting information). In‐hospital consultant continuity was associated with an increased risk of urgent readmission (adj‐HR 1.10, 95% CI, 1.01‐1.20). The association between pre‐admission physician continuity and time to urgent readmission did not interact significantly with patient age, LACE index score, or number of previous admissions.
Discussion
This large, prospective cohort study measured the independent association of several provider and information continuity measures with important outcomes in patients discharged from hospital. After adjusting for potential confounders, we found that increased continuity with physicians who regularly cared for the patient prior to the admission was significantly and independently associated with a decreased risk of urgent readmission. Our data suggest that continuity with the hospital physician did not independently influence the risk of patient death or urgent readmission after discharge.
Although hospital physician continuity did not significantly change patient outcomes, we found that follow‐up with a physician who regularly treated the patient prior to their admission was associated with a significantly decreased risk of urgent readmission. This could reflect the important role that a patient's regular physician plays in their health care. Other studies have shown a positive association between continuity with a regular physician and improved outcomes including decreased emergency room utilization7, 8 and decreased hospitalization.10, 11
We were somewhat disappointed that information continuity was not independently associated with improved patient outcomes. Information continuity is likely more amenable to modification than is provider continuity. Of course, our study findings do not mean that information continuity does not improve patient outcomes, as in other studies.23, 33 Instead, our results could reflect that we solely measured the availability of information to physicians. Future studies that measure the quality, relevance, and actual utilization of patient information will be better able to discern the influence of information continuity on patient outcomes.
We believe that our study was methodologically strong and unique. We captured both provider and information continuity in a large group of representative patients using a broad range of measures that captured continuity's diverse components including both provider and information continuity. The continuity measures were expressed and properly analyzed as time‐dependent variables in a multivariate model.34 Our analysis controlled for important potential confounders. Our follow‐up and data collection was rigorous with 96.1% of our study group having complete follow‐up. Finally, the analysis used multiple imputation to appropriately handle missing data in the one incomplete variable (post‐discharge information continuity).3537
Several limitations of our study should be kept in mind. We are uncertain how our results might generalize to patients discharged from obstetrical or psychiatric services or people in other health systems. Our analysis had to exclude patients with less than two physician visits after discharge since this was the minimum required to calculate postdischarge physician and information continuity. Data collection for postdischarge information continuity was incomplete with data missing for 19.0% of all 15 401 visits in the original cohort.38 However, a response rate of 81.0% is very good39 when compared to other survey‐based studies40 and we accounted for the missing data using multiple imputation methods. The primary outcomes of our studytime to death or urgent readmissionmay be relatively insensitive to modification of quality of care, which is presumably improved by increased continuity.41 For example, Clarke found that the majority of readmissions in all patient groups were unavoidable with 94% of medical readmissions 1 month postdischarge judged to be unavoidable.42 Future studies regarding the effects of continuity could focus on its association with other outcomes that are more reflective of quality of care such as the risk of adverse events or medical error.21 Such outcomes would presumably be more sensitive to improved quality of care from increased continuity.
We believe that our study's major limitation was its inability to establish a causal association between continuity and patient outcomes. Our finding that increased consultant continuity was associated with an increased risk of poor outcomes highlights this concern. Presumably, patient follow‐up with a hospital consultant indicates a disease status with a high risk of bad patient outcomesa risk that is not entirely accounted for by the covariates used in this study. If we accept that unresolved confounding explains this association, the same could also apply to the association between preadmission physician continuity and improved outcomes. Perhaps patients who are doing well after discharge from hospital are able to return to their regular physician. Our analysis would therefore identify an association between increased preadmission physician continuity and improved patient outcomes. Analyses could also incorporate more discriminative measures of severity of hospital illness, such as those developed by Escobar et al.43 Since patients may experience health events after their discharge from hospital that could influence outcomes, recording these and expressing them in the study model as time‐dependent covariates will be important. Finally, similar to the classic study by Wasson et al.44 in 1984, a proper randomized trial that measures the effect of a continuity‐building intervention on both continuity of care and patient outcomes would help determine how continuity influences outcomes.
In conclusion, after discharge from hospital, increased continuity with physicians who routinely care for the patient is significantly and independently associated with a decreased risk of urgent readmission. Continuity with the hospital physician after discharge did not independently influence the risk of patient death or urgent readmission in our study. Further research is required to determine the causal association between preadmission physician continuity and improved outcomes. Until that time, clinicians should strive to optimize continuity with physicians their patients have seen prior to the hospitalization.
Hospitalists are common in North America.1, 2 Hospitalists have been associated with a range of beneficial outcomes including decreased length of stay.3, 4 A primary concern of the hospitalist model is its potential detrimental effect on continuity of care5 partly because patients are often not seen by their hospitalists after discharge.
Continuity of care6 is primarily composed of provider continuity (an ongoing relationship between a patient and a particular provider over time) and information continuity (availability of data from prior events for subsequent patient encounters).6 The association between continuity of care and patient outcomes has been quantified in many studies.720 However, the relationship of continuity and outcomes is especially relevant after discharge from the hospital since this is a time when patients have a high risk of poor patient outcomes21 and poor provider22 and information continuity.2325
The association between continuity and outcomes after hospital discharge has been directly quantified in 2 studies. One found that patients seen by a physician who treated them in the hospital had a significant adjusted relative risk reduction in 30‐day death or readmission of 5% and 3%, respectively.22 The other study found that patients discharged from a general medicine ward were less likely to be readmitted if they were seen by physicians who had access to their discharge summary.23 However, neither of these studies concurrently measured the influence of provider and information continuity on patient outcomes.
Determining whether and how continuity of care influences patient outcomes after hospital discharge is essential to improve health care in an evidence‐based fashion. In addition, the influence that hospital physician follow‐up has on patient outcomes can best be determined by measuring provider and information continuity in patients after hospital discharge. This study sought to measure the independent association of several provider and information continuity measures on death or urgent readmission after hospital discharge.
Methods
Study Design
This was a multicenter prospective cohort study of consecutive patients discharged to the community from the medical or surgical services of 11 Ontario hospitals (6 university‐affiliated hospitals and 5 community hospitals) in 5 cities after an elective or emergency hospitalization. Patients were invited to participate in the study if they were cognitively intact, had a telephone, and provided written informed consent. Patients were excluded if they were less than 18 years old, were discharged to nursing homes, or were not proficient in English and did not have someone to help communicate with study staff. Enrolled patients were excluded from the analysis if they had less than 2 physician visits prior to one of the study's outcomes or the end of patient observation (which was 6 months postdischarge). This final exclusion criterion was necessary since 2 continuity measures (including postdischarge physician continuity and postdischarge information continuity) were incalculable with less than 2 physician visits during follow‐up (Supporting information). The study was approved by the research ethics board of each participating hospital.
Data Collection
Prior to hospital discharge, patients were interviewed by study personnel to identify their baseline functional status, their living conditions, all physicians who regularly treated the patient prior to admission (including both family physicians and consultants), and chronic medical conditions. The latter were confirmed by a review of the patient's chart and hospital discharge summary, when available. Patients also provided principal contacts whom we could contact in the event patients could not be reached. The chart and discharge summary were also used to identify diagnoses in hospitalincluding complications (diagnoses arising in the hospital)and medications at discharge.
Patients or their designated contacts were telephoned 1, 3, and 6 months after hospital discharge to identify the date and the physician of all postdischarge physician visits. For each postdischarge physician visit, we determined whether the physician had access to a discharge summary for the index hospitalization. We also determined the availability of information from all previous postdischarge visits that the patient had with other physicians. The methods used to collect these data were previously detailed.26 Briefly, we used three complementary methods to elicit this information from each follow‐up physician. First, patients gave the physician a survey on which the physician listed all prior visits with other doctors for which they had information. If this survey was not returned, we faxed the survey to the physician. If the faxed survey was not returned, we telephoned the physician or their office staff and administered the survey over the telephone.
Continuity Measures
We measured components of both provider and information continuity. For the posthospitalization period, we measured provider continuity for physicians who had provided patient care during three distinct phases: the prehospital period; the hospital period; and the postdischarge period. Prehospital physicians were those classified by the patient as their regular physician(s) (defined as physiciansboth family physicians and consultantsthat they had seen in the past and were likely to see again in the future). Hospital provider continuity was divided into 2 components: hospital physician continuity (ie, the most responsible physician in the hospital); and hospital consultant continuity (ie, another physician who consulted on the patient during admission). Information continuity was divided into discharge summary continuity and postdischarge visit information continuity.
We quantified provider and information continuity using Breslau's Usual Provider of Continuity (UPC)27 measure. It is a widely used and validated continuity measure whose values are meaningful and interpretable.6 The UPC measures the proportion of visits with the physician of interest (for provider continuity) or the proportion of visits having the information of interest (for information continuity). The UPC was calculated as: $${\rm UPC} = {\rm n}_{\rm i} / {\rm N}$$
As the formulae in the supporting information suggest, all continuity measures were incalculable prior to the first postdischarge visit and all continuity measures changed value at each visit during patient observation. In addition, a particular physician visit could increase multiple continuity measures simultaneously. For example, a visit with a physician who was the hospital physician and who regularly treated the patient prior to the hospitalization would increase both hospital and prehospital provider continuity. If the patient had previously seen the physician after discharge, the visit would also increase postdischarge physician continuity.
Study Outcomes
Outcomes for the study included time to all‐cause death and time to all‐cause, urgent readmission. To be classified as urgent, readmissions could not be arranged when the patient was originally discharged from hospital or more than 4 weeks prior to the readmission. All hospital admissions meeting these criteria during the 6 month study period were labeled in this study as urgent readmissions even if they were unrelated to the index admission.
Principal contacts were called if we were unable to reach the patient to determine their outcomes. If the patient's vital status remained unclear, we contacted the Office of the Provincial Registrar to determine if and when the patient died during the 6 months after discharge from hospital.
Analysis
Outcome incidence densities and 95% confidence intervals [CIs] were calculated using PROC GENMOD in SAS to account for clustering of patients in hospitals. We used multivariate proportional hazards modeling to determine the independent association of provider and information continuity measures with time to death and time to urgent readmission. Patient observation started when patients were discharged from the hospital. Patient observation ended at the earliest of the following: death; urgent readmission to the hospital; end of follow‐up (which was 6 months after discharge from the hospital) or loss to follow‐up. Because hospital consultant continuity was very highly skewed (95.6% of patients had a value of 0; mean value of 0.016; skewness 6.9), it was not included in the primary regression models but was included in a sensitivity analysis.
To adjust for potential confounders in the association between continuity and the outcomes, our model included all factors that were independently associated with either the outcome or any continuity measure. Factors associated with death or urgent readmission were summarized using the LACE index.29 This index combines a patient's hospital length of stay, admission acuity, patient comorbidity (measured with the Charlson Score30 using updated disease category weights by Schneeweiss et al.),31 and emergency room utilization (measured as the number of visits in the 6 months prior to admission) into a single number ranging from 0 to 19. The LACE index was moderately discriminative and highly accurate at predicting 30‐day death or urgent readmission.29 In a separate study,28 we found that the following factors were independently associated with at least one of the continuity measures: patient age; patient sex; number of admissions in previous 6 months; number of regular treating physicians prior to admission; hospital service (medicine vs. surgery); and number of complications in the hospital (defined as new problems arising after admission to hospital). By including all factors that were independently associated with either the outcome or continuity, we controlled for all measured factors that could act as confounders in the association between continuity and outcomes. We accounted for the clustered study design by using conditional proportional hazards models that stratified by hospitals.32 Analytical details are given in the supporting information.
Results
Between October 2002 and July 2006, we enrolled 5035 patients from 11 hospitals (Figure 1). Of the 5035 patients, 274 (5.4%) had no follow up interview with study personnel. A total of 885 (17.6%) had fewer than 2 post discharge physician visits and were not included in the continuity analyses. This left 3876 patients for this analysis (77.0% of the original cohort), of which 3727 had complete follow up (96.1% of the study cohort). A total of 531 patients (10.6% of the original cohort) had incomplete follow‐up because: 342 (6.8%) were lost to follow‐up; 172 (3.4%) refused participation; and 24 (0.5%) were transferred into a nursing home during the first month of observation.


The 3876 study patients are described in Table 1. Overall, these people had a mean age of 62 and most commonly had no physical limitations. Almost a third of patients had been admitted to the hospital in the previous 6 months. A total of 7.6% of patients had no regular prehospital physician while 5.8% had more than one regular prehospital physician. Patients were evenly split between acute and elective admissions and 12% had a complication during their admission. They were discharged after a median of 4 days on a median of 4 medications.
| Factor | Value | Death or Urgent Readmission | All (n = 3876) | |
|---|---|---|---|---|
| No (n = 3491) | Yes (n = 385) | |||
| ||||
| Mean patient age, years (SD) | 61.59 16.16 | 67.70 15.53 | 62.19 16.20 | |
| Female (%) | 1838 (52.6) | 217 (56.4) | 2055 (53.0) | |
| Lives alone (%) | 791 (22.7) | 107 (27.8) | 898 (23.2) | |
| # activities of daily living requiring aids (%) | 0 | 3277 (93.9) | 354 (91.9) | 3631 (93.7) |
| 1 | 125 (3.6) | 20 (5.2) | 145 (3.7) | |
| >1 | 89 (2.5) | 11 (2.8) | 100 (2.8) | |
| # physicians who see patient regularly (%) | 0 | 241 (6.9) | 22 (5.7) | 263 (6.8) |
| 1 | 3060 (87.7) | 333 (86.5) | 3393 (87.5) | |
| 2 | 150 (4.3) | 21 (5.5) | 171 (4.4) | |
| >2 | 281 (8.0) | 31 (8.0) | 312 (8.0) | |
| # admissions in previous 6 months (%) | 0 | 2420 (69.3) | 222 (57.7) | 2642 (68.2) |
| 1 | 833 (23.9) | 103 (26.8) | 936 (24.1) | |
| >1 | 238 (6.8) | 60 (15.6) | 298 (7.7) | |
| Index hospitalization description | ||||
| Number of discharge medications (IQR) | 4 (2‐7) | 6 (3‐9) | 4 (2‐7) | |
| Admitted to medical service (%) | 1440 (41.2) | 231 (60.0) | 1671 (43.1) | |
| Acute diagnoses: | ||||
| CAD (%) | 238 (6.8) | 23 (6.0) | 261 (6.7) | |
| Neoplasm of unspecified nature (%) | 196 (5.6) | 35 (9.1) | 231 (6.0) | |
| Heart failure (%) | 127 (3.6) | 38 (9.9) | 165 (4.3) | |
| Acute procedures | ||||
| CABG (%) | 182 (5.2) | 14 (3.6) | 196 (5.1) | |
| Total knee arthoplasty (%) | 173 (5.0) | 10 (2.6) | 183 (4.7) | |
| Total hip arthroplasty (%) | 118 (3.4) | (0.5) | 120 (3.1) | |
| Complication during admission (%) | 403 (11.5) | 63 (16.4) | 466 (12.0) | |
| LACE index: mean (SD) | 8.0 (3.6) | 10.3 (3.8) | 8.2 (3.7) | |
| Length of stay in days: median (IQR) | 4 (2‐7) | 6 (3‐10) | 4 (2‐8) | |
| Acute/emergent admission (%) | 1851 (53.0) | 272 (70.6) | 2123 (54.8) | |
| Charlson score (%) | 0 | 2771 (79.4) | 241 (62.6) | 3012 (77.7) |
| 1 | 103 (3.0) | 17 (4.4) | 120 (3.1) | |
| 2 | 446 (12.8) | 86 (22.3) | 532 (13.7) | |
| >2 | 171 (4.9) | 41 (10.6) | 212 (5.5) | |
| Emergency room use (# visits/ year) (%) | 0 | 2342 (67.1) | 190 (49.4) | 2532 (65.3) |
| 1 | 761 (21.8) | 101 (26.2) | 862 (22.2) | |
| >1 | 388 (11.1) | 94 (24.4) | 482 (12.4) | |
Patients were observed in the study for a median of 175 days (interquartile range [IQR] 175‐178). During this time they had a median of 4 physician visits (IQR 3‐6). The first postdischarge physician visit occurred a median of 10 days (IQR 6‐18) after discharge from hospital.
Continuity Measures
Table 2 summarizes all continuity scores. Since continuity scores varied significantly over time,28 Table 2 provides continuity scores on the last day of patient observation. Preadmission provider, postdischarge provider, and discharge summary continuity all had similar values and distributions with median values ranging between 0.444 and 0.571. 1797 (46.4%) patients had a hospital physician provider continuity scorae of 0.
| Minimum | 25th Percentile | Median | 75th Percentile | Maximum | |
|---|---|---|---|---|---|
| Provider continuity | |||||
| A: Pre‐admission physician | 0 | 0.143 | 0.444 | 0.667 | 1.000 |
| B: Hospital physician | 0 | 0 | 0.143 | 0.400 | 1.000 |
| C: Post‐discharge physician | 0 | 0.333 | 0.571 | 0.750 | 1.000 |
| Information continuity | |||||
| D: Discharge summary | 0 | 0.095 | 0.500 | 0.800 | 1.000 |
| E: Post‐discharge information | 0 | 0 | 0.182 | 0.500 | 1.000 |
Study Outcomes
During a median of 175 days of observation, 45 patients died (event rate 2.6 events per 100 patient‐years observation [95% CI 2.0‐3.4]) and 340 patients were urgently readmitted (event rate 19.6 events per 100 patient‐years observation [95% CI 15.9‐24.3]). Figure 2 presents the survival curves for time to death and time to urgent readmission. The hazard of death was consistent through the observation period but the risk of urgent readmission decreased slightly after 90 days postdischarge.
Association Between Continuity and Outcomes
Table 3 summarizes the association between provider and information continuity with study outcomes. No continuity measure was associated with time to death by itself (Table 3, column A) or with the other continuity measures (Table 3, column B). Preadmission physician continuity was associated with a significantly decreased risk of urgent readmission. When the proportion of postdischarge visits with a prehospital physician increased by 10%, the adjusted risk of urgent readmission decreased by 6% (adjusted hazards ratio (adj‐HR)) of 0.94 (95% CI, 0.91‐0.98). None of the other continuity measuresincluding hospital physicianwere significantly associated with urgent readmission either by themselves (Table 3, column A) or after adjusting for other continuity measures (Table 3, column B).
| Outcome | ||||||||
|---|---|---|---|---|---|---|---|---|
| Death (95% CI) | Urgent Readmission (95% CI) | |||||||
| A: Adjusted for Other Confounders Only | B: Adjusted for Other Confounders and Continuity Measures | A: Adjusted for Other Confounders Only | B: Adjusted for Other Confounders and Continuity Measures | |||||
| ||||||||
| Provider continuity | ||||||||
| A: Pre‐admission physician | 1.03 | (0.95, 1.12) | 1.06 | (0.95, 1.18) | 0.95 | (0.92, 0.98) | 0.94 | (0.91, 0.98) |
| B: Hospital physician | 0.87 | (0.74, 1.02) | 0.86 | (0.70, 1.03) | 0.98 | (0.94, 1.02) | 0.97 | (0.92, 1.01) |
| C: Post‐discharge physician | 0.97 | (0.89, 1.06) | 0.93 | (0.84, 1.04) | 0.98 | (0.95, 1.01) | 0.98 | (0.94, 1.02) |
| Information continuity | ||||||||
| D: Discharge Summary | 0.96 | (0.89, 1.04) | 0.94 | (0.87, 1.03) | 1.01 | (0.98, 1.04) | 1.02 | (0.99, 1.05) |
| E: Post‐discharge information | 1.01 | (0.94, 1.08) | 1.03 | (0.95, 1.11) | 1.00 | (0.97, 1.03) | 1.03 | (0.95, 1.11) |
| Other confounders | ||||||||
| Patient age in decades* | 1.43 | (1.13, 1.82) | 1.18 | (1.10, 1.28) | ||||
| Female | 1.50 | (0.81, 2.77) | 1.16 | (0.94, 1.44) | ||||
| # physicians who see patient regularly | ||||||||
| 1 | 1.46 | (0.92, 2.34) | ||||||
| 2 | 2.17 | (1.11, 4.26) | ||||||
| >2 | 3.71 | (1.55, 8.88) | ||||||
| Complications during admission | ||||||||
| 1 | 1.38 | (0.61, 3.10) | 0.81 | (0.55, 1.17) | ||||
| >1 | 1.01 | (0.28, 3.58) | 0.91 | (0.56, 1.48) | ||||
| # admissions in previous 6 months | ||||||||
| 1 | 1.27 | (0.59, 2.70) | 1.34 | (1.02, 1.76) | ||||
| >1 | 1.42 | (0.55, 3.67) | 1.78 | (1.26, 2.51) | ||||
| LACE index* | 1.16 | (1.06, 1.26) | 1.10 | (1.07, 1.14) | ||||
Increased patient age and increased LACE index score were both strongly associated with an increased risk of death (adj‐HR 1.43 [1.13‐1.82] and 1.16 [1.06‐1.26], respectively) and urgent readmission (adj‐HR 1.18 [1.10‐1.28] and 1.10 [1.07‐1.14], respectively). Hospitalization in the 6 months prior to admission significantly increased the risk of urgent readmission but not death. The risk of urgent readmission increased significantly as the number of regular prehospital physicians increased.
Sensitivity Analyses
Our study conclusions did not change in the sensitivity analyses. The number of postdischarge physician visits (expressed as a time‐dependent covariate) was not associated with either death or with urgent readmission and preadmission physician continuity remained significantly associated with time to urgent readmission (supporting information). Adding consultant continuity to the model also did not change our results (supporting information). In‐hospital consultant continuity was associated with an increased risk of urgent readmission (adj‐HR 1.10, 95% CI, 1.01‐1.20). The association between pre‐admission physician continuity and time to urgent readmission did not interact significantly with patient age, LACE index score, or number of previous admissions.
Discussion
This large, prospective cohort study measured the independent association of several provider and information continuity measures with important outcomes in patients discharged from hospital. After adjusting for potential confounders, we found that increased continuity with physicians who regularly cared for the patient prior to the admission was significantly and independently associated with a decreased risk of urgent readmission. Our data suggest that continuity with the hospital physician did not independently influence the risk of patient death or urgent readmission after discharge.
Although hospital physician continuity did not significantly change patient outcomes, we found that follow‐up with a physician who regularly treated the patient prior to their admission was associated with a significantly decreased risk of urgent readmission. This could reflect the important role that a patient's regular physician plays in their health care. Other studies have shown a positive association between continuity with a regular physician and improved outcomes including decreased emergency room utilization7, 8 and decreased hospitalization.10, 11
We were somewhat disappointed that information continuity was not independently associated with improved patient outcomes. Information continuity is likely more amenable to modification than is provider continuity. Of course, our study findings do not mean that information continuity does not improve patient outcomes, as in other studies.23, 33 Instead, our results could reflect that we solely measured the availability of information to physicians. Future studies that measure the quality, relevance, and actual utilization of patient information will be better able to discern the influence of information continuity on patient outcomes.
We believe that our study was methodologically strong and unique. We captured both provider and information continuity in a large group of representative patients using a broad range of measures that captured continuity's diverse components including both provider and information continuity. The continuity measures were expressed and properly analyzed as time‐dependent variables in a multivariate model.34 Our analysis controlled for important potential confounders. Our follow‐up and data collection was rigorous with 96.1% of our study group having complete follow‐up. Finally, the analysis used multiple imputation to appropriately handle missing data in the one incomplete variable (post‐discharge information continuity).3537
Several limitations of our study should be kept in mind. We are uncertain how our results might generalize to patients discharged from obstetrical or psychiatric services or people in other health systems. Our analysis had to exclude patients with less than two physician visits after discharge since this was the minimum required to calculate postdischarge physician and information continuity. Data collection for postdischarge information continuity was incomplete with data missing for 19.0% of all 15 401 visits in the original cohort.38 However, a response rate of 81.0% is very good39 when compared to other survey‐based studies40 and we accounted for the missing data using multiple imputation methods. The primary outcomes of our studytime to death or urgent readmissionmay be relatively insensitive to modification of quality of care, which is presumably improved by increased continuity.41 For example, Clarke found that the majority of readmissions in all patient groups were unavoidable with 94% of medical readmissions 1 month postdischarge judged to be unavoidable.42 Future studies regarding the effects of continuity could focus on its association with other outcomes that are more reflective of quality of care such as the risk of adverse events or medical error.21 Such outcomes would presumably be more sensitive to improved quality of care from increased continuity.
We believe that our study's major limitation was its inability to establish a causal association between continuity and patient outcomes. Our finding that increased consultant continuity was associated with an increased risk of poor outcomes highlights this concern. Presumably, patient follow‐up with a hospital consultant indicates a disease status with a high risk of bad patient outcomesa risk that is not entirely accounted for by the covariates used in this study. If we accept that unresolved confounding explains this association, the same could also apply to the association between preadmission physician continuity and improved outcomes. Perhaps patients who are doing well after discharge from hospital are able to return to their regular physician. Our analysis would therefore identify an association between increased preadmission physician continuity and improved patient outcomes. Analyses could also incorporate more discriminative measures of severity of hospital illness, such as those developed by Escobar et al.43 Since patients may experience health events after their discharge from hospital that could influence outcomes, recording these and expressing them in the study model as time‐dependent covariates will be important. Finally, similar to the classic study by Wasson et al.44 in 1984, a proper randomized trial that measures the effect of a continuity‐building intervention on both continuity of care and patient outcomes would help determine how continuity influences outcomes.
In conclusion, after discharge from hospital, increased continuity with physicians who routinely care for the patient is significantly and independently associated with a decreased risk of urgent readmission. Continuity with the hospital physician after discharge did not independently influence the risk of patient death or urgent readmission in our study. Further research is required to determine the causal association between preadmission physician continuity and improved outcomes. Until that time, clinicians should strive to optimize continuity with physicians their patients have seen prior to the hospitalization.
- Society of Hospital Medicine.2009.Ref Type: Internet Communication.
- ,,,.The status of hospital medicine groups in the United States.J Hosp Med.2006;1:75–80.
- ,.The hospitalist movement 5 years later. [see comment].JAMA.2002;287:487–494. [Review]
- ,,,.Hospitalists and the practice of inpatient medicine: results of a survey of the National Association of Inpatient Physicians. [see comment].Ann Intern Med.1999;130:343–349.
- ,,,.Primary care physician attitudes regarding communication with hospitalists.Am J Med.2001;111:15S–20S.
- ,,.Defusing the confusion: concepts and measures of continuity of healthcare.Ottawa,Canadian Health Services Research Foundation. Ref Type: Report.2002;1–50.
- ,,,,.Association between infant continuity of care and pediatric emergency department utilization.Pediatrics.2004;113:738–741.
- ,,,,.Is greater continuity of care associated with less emergency department utilization?Pediatrics.1999;103:738–742.
- ,,,,.Association of lower continuity of care with greater risk of emergency department use and hospitalization in children.Pediatrics.2001;107:524–529.
- ,,The role of provider continuity in preventing hospitalizations.Arch Fam Med.1998;7:352–357.
- ,.The importance of continuity of care in the likelihood of future hospitalization: is site of care equivalent to a primary clinician?Am J Public Health.1998;88:1539–1541.
- ,,,.Exploration of the relationship between continuity, trust in regular doctors and patient satisfaction with consultations with family doctors.Scand J Prim Health Care.2003;21:27–32.
- ,,,,.Longitudinal continuity of care is associated with high patient satisfaction with physical therapy.Phys Ther.2005;85:1046–1052.
- ,,,,.Provider continuity and outcomes of care for persons with schizophrenia.Ment Health Serv Res.2000;V2:201–211.
- ,,,,.Continuity of care is associated with well‐coordinated care.Ambul Pediatr.2003;3:82–86.
- ,,.The impact of insurance type and forced discontinuity on the delivery of primary care. [see comments.].J Fam Pract.1997;45:129–135.
- .Measuring attributes of primary care: development of a new instrument.J Fam Pract.1997;45:64–74.
- .Continuity of care during pregnancy: the effect of provider continuity on outcome.J Fam Pract.1985;21:375–380.
- ,,,,,.Physician‐patient relationship and medication compliance: a primary care investigation.Ann Fam Med.2004;2:455–461.
- ,,,.Continuity of care and cardiovascular risk factor management: does care by a single clinician add to informational continuity provided by electronic medical records?Am J Manag Care.2005;11:689–696.
- ,,,,.The incidence and severity of adverse events affecting patients after discharge from the hospital.Ann Intern Med.2003;138:161–167.
- ,,,.Continuity of care and patient outcomes after hospital discharge.J Gen lntern Med.2004;19:624–645.
- ,,,.Effect of discharge summary availability during post‐discharge visits on hospital readmission.J Gen Intern Med.2002;17:186–192.
- ,,, et al.Association of communication between hospital‐based physicians and primary care providers with patient outcomes.[see comment].J Gen Intern Med2009;24(3):381–386.
- ,,,,,.Deficits in communication and information transfer between hospital‐based and primary care physicians: implications for patient safety and continuity of care.JAMA.2007;297:831–841.
- ,,, et al.Information exchange among physicians caring for the same patient in the community.Can Med Assoc J.2008;179:1013–1018.
- ,.Continuity of care in a university‐based practice.J Med Educ.1975;965–969.
- ,,, et al.Provider and information continuity after discharge from hospital: a prospective cohort study.2009. Ref Type: Unpublished Work.
- ,,, et al.Derivation and validation of the LACE index to predict early death or unplanned readmission after discharge from hospital to the community.CMAJ. (In press)
- ,,,.A new method of classifying prognostic comorbidity in longitudinal studies: development and validation.J Chronic Dis.1987;40:373–383.
- ,,,.Improved comorbidity adjustment for predicting mortality in Medicare populations.Health Serv Res.2003;38(4):1103–1120.
- ,.Modelling clustered survival data from multicentre clinical trials.Stat Med.2004;23:369–388.
- ,,,.Prevalence of information gaps in the emergency department and the effect on patient outcomes.CMAJ.2003;169:1023–1028.
- ,,,.Time‐dependent bias due to improper analytical methodology is common in prominent medical journals.J Clin Epidemiol.2004;57:672–682.
- .What do we do with missing data? Some options for analysis of incomplete data.Annu Rev Public Health.2004;25:99–117.
- ,,,.Survival estimates of a prognostic classification depended more on year of treatment than on imputation of missing values.J Clin Epidemiol.2006;59:246–253. [Review]
- .Bias arising from missing data in predictive models.[see comment].J Clin Epidemiol.2006;59:1115–1123.
- ,,, et al.Information exchange among physicians caring for the same patient in the community.CMAJ.2008;179:1013–1018.
- .Survey Research Methods.2nd ed.,Beverly Hills:Sage;1993.
- ,,.Response rates to mail surveys published in medical journals.J Clin Epidemiol.1997;50:1129–1136.
- .Readmission of patients to hospital: still ill defined and poorly understood.Int J Qual Health Care.2001;13:177–179.
- .Are readmissions avoidable?Br Med J.1990;301:1136–1138.
- ,,,,,.Risk‐adjusting hospital inpatient mortality using automated inpatient, outpatient, and laboratory databases.Med Care.2008;46:232–239.
- ,,, et al.Continuity of outpatient medical care in elderly men. A randomized trial.JAMA.1984;252:2413–2417.
- Society of Hospital Medicine.2009.Ref Type: Internet Communication.
- ,,,.The status of hospital medicine groups in the United States.J Hosp Med.2006;1:75–80.
- ,.The hospitalist movement 5 years later. [see comment].JAMA.2002;287:487–494. [Review]
- ,,,.Hospitalists and the practice of inpatient medicine: results of a survey of the National Association of Inpatient Physicians. [see comment].Ann Intern Med.1999;130:343–349.
- ,,,.Primary care physician attitudes regarding communication with hospitalists.Am J Med.2001;111:15S–20S.
- ,,.Defusing the confusion: concepts and measures of continuity of healthcare.Ottawa,Canadian Health Services Research Foundation. Ref Type: Report.2002;1–50.
- ,,,,.Association between infant continuity of care and pediatric emergency department utilization.Pediatrics.2004;113:738–741.
- ,,,,.Is greater continuity of care associated with less emergency department utilization?Pediatrics.1999;103:738–742.
- ,,,,.Association of lower continuity of care with greater risk of emergency department use and hospitalization in children.Pediatrics.2001;107:524–529.
- ,,The role of provider continuity in preventing hospitalizations.Arch Fam Med.1998;7:352–357.
- ,.The importance of continuity of care in the likelihood of future hospitalization: is site of care equivalent to a primary clinician?Am J Public Health.1998;88:1539–1541.
- ,,,.Exploration of the relationship between continuity, trust in regular doctors and patient satisfaction with consultations with family doctors.Scand J Prim Health Care.2003;21:27–32.
- ,,,,.Longitudinal continuity of care is associated with high patient satisfaction with physical therapy.Phys Ther.2005;85:1046–1052.
- ,,,,.Provider continuity and outcomes of care for persons with schizophrenia.Ment Health Serv Res.2000;V2:201–211.
- ,,,,.Continuity of care is associated with well‐coordinated care.Ambul Pediatr.2003;3:82–86.
- ,,.The impact of insurance type and forced discontinuity on the delivery of primary care. [see comments.].J Fam Pract.1997;45:129–135.
- .Measuring attributes of primary care: development of a new instrument.J Fam Pract.1997;45:64–74.
- .Continuity of care during pregnancy: the effect of provider continuity on outcome.J Fam Pract.1985;21:375–380.
- ,,,,,.Physician‐patient relationship and medication compliance: a primary care investigation.Ann Fam Med.2004;2:455–461.
- ,,,.Continuity of care and cardiovascular risk factor management: does care by a single clinician add to informational continuity provided by electronic medical records?Am J Manag Care.2005;11:689–696.
- ,,,,.The incidence and severity of adverse events affecting patients after discharge from the hospital.Ann Intern Med.2003;138:161–167.
- ,,,.Continuity of care and patient outcomes after hospital discharge.J Gen lntern Med.2004;19:624–645.
- ,,,.Effect of discharge summary availability during post‐discharge visits on hospital readmission.J Gen Intern Med.2002;17:186–192.
- ,,, et al.Association of communication between hospital‐based physicians and primary care providers with patient outcomes.[see comment].J Gen Intern Med2009;24(3):381–386.
- ,,,,,.Deficits in communication and information transfer between hospital‐based and primary care physicians: implications for patient safety and continuity of care.JAMA.2007;297:831–841.
- ,,, et al.Information exchange among physicians caring for the same patient in the community.Can Med Assoc J.2008;179:1013–1018.
- ,.Continuity of care in a university‐based practice.J Med Educ.1975;965–969.
- ,,, et al.Provider and information continuity after discharge from hospital: a prospective cohort study.2009. Ref Type: Unpublished Work.
- ,,, et al.Derivation and validation of the LACE index to predict early death or unplanned readmission after discharge from hospital to the community.CMAJ. (In press)
- ,,,.A new method of classifying prognostic comorbidity in longitudinal studies: development and validation.J Chronic Dis.1987;40:373–383.
- ,,,.Improved comorbidity adjustment for predicting mortality in Medicare populations.Health Serv Res.2003;38(4):1103–1120.
- ,.Modelling clustered survival data from multicentre clinical trials.Stat Med.2004;23:369–388.
- ,,,.Prevalence of information gaps in the emergency department and the effect on patient outcomes.CMAJ.2003;169:1023–1028.
- ,,,.Time‐dependent bias due to improper analytical methodology is common in prominent medical journals.J Clin Epidemiol.2004;57:672–682.
- .What do we do with missing data? Some options for analysis of incomplete data.Annu Rev Public Health.2004;25:99–117.
- ,,,.Survival estimates of a prognostic classification depended more on year of treatment than on imputation of missing values.J Clin Epidemiol.2006;59:246–253. [Review]
- .Bias arising from missing data in predictive models.[see comment].J Clin Epidemiol.2006;59:1115–1123.
- ,,, et al.Information exchange among physicians caring for the same patient in the community.CMAJ.2008;179:1013–1018.
- .Survey Research Methods.2nd ed.,Beverly Hills:Sage;1993.
- ,,.Response rates to mail surveys published in medical journals.J Clin Epidemiol.1997;50:1129–1136.
- .Readmission of patients to hospital: still ill defined and poorly understood.Int J Qual Health Care.2001;13:177–179.
- .Are readmissions avoidable?Br Med J.1990;301:1136–1138.
- ,,,,,.Risk‐adjusting hospital inpatient mortality using automated inpatient, outpatient, and laboratory databases.Med Care.2008;46:232–239.
- ,,, et al.Continuity of outpatient medical care in elderly men. A randomized trial.JAMA.1984;252:2413–2417.
Copyright © 2010 Society of Hospital Medicine