User login
Meta-analysis: Its strengths and limitations
The amount of information generated in medical research is becoming overwhelming, even for experienced researchers. New studies are constantly being published, and clinicians are finding it nearly impossible to stay current, even in their own area of specialty.
To help make sense of the information, we are seeing more and more review articles that pool the results of multiple studies. When certain principles are followed and the data are quantitatively analyzed, these reviews are called meta-analyses. A PubMed search of the word “meta-analysis” in the title yielded 1,473 articles in the year 2007.
Combining available information to generate an integrated result seems reasonable and can save a considerable amount of resources. Nowadays, meta-analyses are being used to design future research, to provide evidence in the regulatory process,1 and even to modify clinical practice.
Meta-analysis is powerful but also controversial—controversial because several conditions are critical to a sound meta-analysis, and small violations of those conditions can lead to misleading results. Summarizing large amounts of varied information using a single number is another controversial aspect of meta-analysis. Under scrutiny, some meta-analyses have been inappropriate, and their conclusions not fully warranted.2,3
This article introduces the basic concepts of meta-analysis and discusses its caveats, with the aim of helping clinicians assess the merits of the results. We will use several recent meta-analyses to illustrate the issues, including a controversial one4 with potentially far-reaching consequences.
OBJECTIVES OF META-ANALYSIS
The main objectives of a meta-analysis are to:
- Summarize and integrate results from a number of individual studies
- Analyze differences in the results among studies
- Overcome small sample sizes of individual studies to detect effects of interest, and analyze end points that require larger sample sizes
- Increase precision in estimating effects
- Evaluate effects in subsets of patients
- Determine if new studies are needed to further investigate an issue
- Generate new hypotheses for future studies.
These lofty objectives can only be achieved when the meta-analysis satisfactorily addresses certain critical issues, which we will discuss next.
CRITICAL ISSUES IN META-ANALYSIS DESIGN
Four critical issues need to be addressed in a meta-analysis:
- Identification and selection of studies
- Heterogeneity of results
- Availability of information
- Analysis of the data.
IDENTIFICATION AND SELECTION OF STUDIES
The outcome of a meta-analysis depends on the studies included. The critical aspect of selecting studies to be included in a meta-analysis consists of two phases. The first is the identification phase or literature search, in which potential studies are identified. In the second phase, further criteria are used to create a list of studies for inclusion. Three insidious problems plague this aspect of meta-analysis: publication bias and search bias in the identification phase, and selection bias in the selection phase. These biases are discussed below.
Publication bias: ‘Positive’ studies are more likely to be printed
Searches of databases such as PubMed or Embase can yield long lists of studies. However, these databases include only studies that have been published. Such searches are unlikely to yield a representative sample because studies that show a “positive” result (usually in favor of a new treatment or against a well-established one) are more likely to be published than those that do not. This selective publication of studies is called publication bias.
In a recent article, Turner et al5 analyzed the publication status of studies of antidepressants. Based on studies registered with the US Food and Drug Administration (FDA), they found that 97% of the positive studies were published vs only 12% of the negative ones. Furthermore, when the nonpublished studies were not included in the analysis, the positive effects of individual drugs increased between 11% and 69%.
One reason for publication bias is that drug manufacturers are not generally interested in publishing negative studies. Another may be that editors favor positive studies because these are the ones that make the headlines and give the publication visibility. In some medical areas, the exclusion of studies conducted in non-English-speaking countries can increase publication bias.6
To ameliorate the effect of publication bias on the results of a meta-analysis, a serious effort should be made to identify unpublished studies. Identifying unpublished studies is easier now, thanks to improved communication between researchers worldwide, and thanks to registries in which all the studies of a certain disease or treatment are reported regardless of the result.
The National Institutes of Health maintains a registry of all the studies it supports, and the FDA keeps a registry and database in which drug companies must register all trials they intend to use in applying for marketing approval or a change in labeling. “Banks” of published and unpublished trials supported by pharmaceutical companies are also available (eg, http://ctr.gsk.co.uk/welcome.asp). The Cochrane collaboration (www.cochrane.org/) keeps records of systematic reviews and meta-analyses of many diseases and procedures.
Search bias: Identifying relevant studies
Even in the ideal case that all relevant studies were available (ie, no publication bias), a faulty search can miss some of them. In searching databases, much care should be taken to assure that the set of key words used for searching is as complete as possible. This step is so critical that most recent meta-analyses include the list of key words used. The search engine (eg, PubMed, Google) is also critical, affecting the type and number of studies that are found.7 Small differences in search strategies can produce large differences in the set of studies found.8
Selection bias: Choosing the studies to be included
The identification phase usually yields a long list of potential studies, many of which are not directly relevant to the topic of the meta-analysis. This list is then subject to additional criteria to select the studies to be included. This critical step is also designed to reduce differences among studies, eliminate replication of data or studies, and improve data quality, and thus enhance the validity of the results.
To reduce the possibility of selection bias in this phase, it is crucial for the criteria to be clearly defined and for the studies to be scored by more than one researcher, with the final list chosen by consensus.9,10 Frequently used criteria in this phase are in the areas of:
- Objectives
- Populations studied
- Study design (eg, experimental vs observational)
- Sample size
- Treatment (eg, type and dosage)
- Criteria for selection of controls
- Outcomes measured
- Quality of the data
- Analysis and reporting of results
- Accounting and reporting of attrition rates
- Length of follow-up
- When the study was conducted.
The objective in this phase is to select studies that are as similar as possible with respect to these criteria. It is a fact that even with careful selection, differences among studies will remain. But when the dissimilarities are large it becomes hard to justify pooling the results to obtain a “unified” conclusion.
In some cases, it is particularly difficult to find similar studies,10,11 and sometimes the discrepancies and low quality of the studies can prevent a reasonable integration of results. In a systematic review of advanced lung cancer, Nicolucci et al12 decided not to pool the results, in view of “systematic qualitative inadequacy of almost all trials” and lack of consistency in the studies and their methods. Marsoni et al13 came to a similar conclusion in attempting to summarize results in advanced ovarian cancer.
Stratification is an effective way to deal with inherent differences among studies and to improve the quality and usefulness of the conclusions. An added advantage to stratification is that insight can be gained by investigating discrepancies among strata.
There are many ways to create coherent subgroups of studies. For example, studies can be stratified according to their “quality,” assigned by certain scoring systems. Commonly used systems award points on the basis of how patients were selected and randomized, the type of blinding, the dropout rate, the outcome measurement, and the type of analysis (eg, intention-to-treat). However, these criteria, and therefore the scores, are somewhat subjective. Moher et al14 expand on this issue.
Large differences in sample sizes among studies are not uncommon and can cause problems in the analysis. Depending on the type of model used (see below), meta-analyses combine results based on the size of each study, but when the studies vary significantly in size, the large studies can still have an unduly large influence on the results. Stratifying by sample size is done sometimes to verify the stability of the results.4
On the other hand, the presence of dissimilarities among studies can have advantages by increasing the generalizability of the conclusions. Berlin and Colditz1 point out that “we gain strength in inference when the range of patient characteristics has been broadened by replicating findings in studies with populations that vary in age range, geographic region, severity of underlying illness, and the like.”
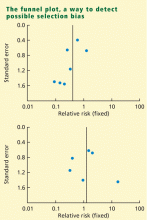
Funnel plot: Detecting biases in the identification and selection of studies
The funnel plot is a technique used to investigate the possibility of biases in the identification and selection phases. In a funnel plot the size of the effect (defined as a measure of the difference between treatment and control) in each study is plotted on the horizontal axis against standard error15 or sample size9 on the vertical axis. If there are no biases, the graph will tend to have a symmetrical funnel shape centered in the average effect of the studies. When negative studies are missing, the graph shows lack of symmetry.
Funnel plots are appealing because they are simple, but their objective is to detect a complex effect, and they can be misleading. For example, lack of symmetry in a funnel plot can also be caused by heterogeneity in the studies.16 Another problem with funnel plots is that they are difficult to interpret when the number of studies is small. In some cases, however, the researcher may not have any option but to perform the analysis and report the presence of bias.11
HETEROGENEITY OF RESULTS
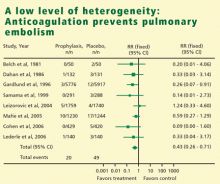
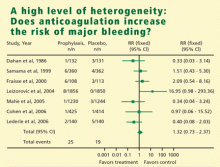
In meta-analysis, heterogeneity refers to the degree of dissimilarity in the results of individual studies. In some cases, the dissimilarities in results can be traced back to inherent differences in the individual studies. In other situations, however, causes for the dissimilarities might not be easy to elucidate. In any case, as the level of heterogeneity increases, the justification for an integrated result becomes more difficult. A tool that is very effective to display the level of heterogeneity is the forest plot. In a forest plot, the estimated effect of each study along with a line representing a confidence interval is drawn. When the effects are similar, the confidence intervals overlap, and heterogeneity is low. The forest plot includes a reference line at the point of no effect (eg, one for relative risks and odds ratios). When some effects lie on opposite sides of the reference line, it means that the studies are contradictory and heterogeneity is high. In such cases, the conclusions of a meta-analysis are compromised.
AVAILABILITY OF INFORMATION
Most reports of individual studies include only summary results, such as means, standard deviations, proportions, odds ratios, and relative risks. Other than the possibility of errors in reporting, the lack of information can severely limit the type of analyses and conclusions that can be reached in a meta-analysis. For example, lack of information from individual studies can preclude the comparison of effects in predetermined subgroups of patients.
The best scenario is when data at the patient level are available. In such cases, the researcher has great flexibility in the analysis of the information. Trivella et al20 performed a meta-analysis of the value of microvessel density in predicting survival in non-small-cell lung cancer. They obtained information on individual patients by contacting research centers directly. The data allowed them to vary the cutoff point to classify microvessel density as high or low and to use statistical methods to ameliorate heterogeneity.
A frequent problem in meta-analysis is the lack of uniformity in how outcomes are measured. In the study by Trivella et al,20 the microvessel density was measured by two methods. The microvessel density was a significant prognostic factor when measured by one of the methods, but not the other.
RANDOMIZED CONTROLLED TRIALS VS OBSERVATIONAL STUDIES
Some researchers believe that meta-analyses should be conducted only on randomized controlled trials.3,21 Their reasoning is that meta-analyses should include only reasonably well-conducted studies to reduce the risk of a misleading conclusion. However, many important diseases can only be studied observationally. If these studies have a certain level of quality, there is no technical reason not to include them in a meta-analysis.
Gillum et al22 performed a meta-analysis published in 2000 on the risk of ischemic stroke in users of oral contraceptives, based on observational studies (since no randomized trials were available). Studies were identified and selected by multiple researchers using strict criteria to make sure that only studies fulfilling certain standards were included. Of 804 potentially relevant studies identified, only 16 were included in the final analysis. A funnel plot showed no evidence of bias and the level of heterogeneity was fairly low. The meta-analysis result confirmed the results of individual studies, but the precision with which the effect was estimated was much higher. The overall relative risk of stroke in women taking oral contraceptives was 2.75, with a 95% confidence interval of 2.24 to 3.38.
A more recent meta-analysis23 (published in 2004) on the same issue found no significant increase in the risk of ischemic stroke with the use of oral contraceptives. Gillum and Johnston24 suggest that the main reason for the discrepancy is the lower amount of estrogen in newer oral contraceptives. They also point out differences in the control groups and study outcomes as reasons for the discrepancies between the two studies.
Bhutta et al25 performed a meta-analysis of case-control (observational) studies of the effect of preterm birth on cognitive and behavioral outcomes. Studies were included only if the children were evaluated after their fifth birthday and the attrition rate was less than 30%. The studies were grouped according to criteria of quality devised specifically for case-control studies. The high-quality studies tended to show a larger effect than the low-quality studies, but the difference was not significant. Seventeen studies were included, and all of them found that children born preterm had lower cognitive scores; the difference was statistically significant in 15 of the studies. As expected, the meta-analysis confirmed these findings (95% confidence interval for the difference 9.2–12.5). The number of patients (1,556 cases and 1,720 controls) in the meta-analysis allowed the researchers to conclude further that the mean cognitive scores were directly proportional to the mean birth weight (R2 = 0.51, P < .001) and gestational age (R2 = 0.49, P < .001).
ANALYSIS OF DATA
There are specific statistical techniques that are used in meta-analysis to analyze and integrate the information. The data from the individual studies can be analyzed using either of two models: fixed effects or random effects.
The fixed-effects model assumes that the treatment effect is the same across studies. This common effect is unknown, and the purpose of the analysis is to estimate it with more precision than in the individual studies.
The random-effects model, on the other hand, assumes that the treatment effect is not the same across studies. The goal is to estimate the average effect in the studies.
In the fixed-effects model, the results of individual studies are pooled using weights that depend on the sample size of the study, whereas in the random-effects model each study is weighted equally. Due to the heterogeneity among studies, the random-effects model yields wider confidence intervals.
Both models have pros and cons. In many cases, the assumption that the treatment effect is the same in all the studies is not tenable, and the random-effects model is preferable. When the effect of interest is large, the results of both models tend to agree, particularly when the studies are balanced (ie, they have a similar number of patients in the treatment group as in the control group) and the study sizes are similar. But when the effect is small or when the level of heterogeneity of the studies is high, the result of the meta-analysis is likely to depend on the model used. In those cases, the analysis should be done and presented using both models.
It is highly desirable for a meta-analysis to include a sensitivity analysis to determine the “robustness” of the results. Two common ways to perform sensitivity analysis are to analyze the data using various methods and to present the results when some studies are removed from the analysis.26 If these actions cause serious changes in the overall results, the credibility of the results is compromised.
The strength of meta-analysis is that, by pooling many studies, the effective sample size is greatly increased, and consequently more variables and outcomes can be examined. For example, analysis in subsets of patients and regression analyses9 that could not be done in individual trials can be performed in a meta-analysis.
A word of caution should be given with respect to larger samples and the possibility of multiple analyses of the data in meta-analysis. Much care must be exercised when examining the significance of effects that are not considered prior to the meta-analysis. The testing of effects suggested by the data and not planned a priori (sometimes called “data-mining”) increases considerably the risk of false-positive results. One common problem with large samples is the temptation to perform many so-called “subgroup analyses” in which subgroups of patients formed according to multiple baseline characteristics are compared.27 The best way to minimize the possibility of false-positive results is to determine the effects to be tested before the data are collected and analyzed. Another method is to adjust the P value according to the number of analyses performed. In general, post hoc analyses should be deemed exploratory, and the reader should be made aware of this fact in order to judge the validity of the conclusion.
META-ANALYSIS OF RARE EVENTS
Lately, meta-analysis has been used to analyze outcomes that are rare and that individual studies were not designed to test. In general, the sample size of individual studies provides inadequate power to test rare outcomes. Adverse events are prime examples of important rare outcomes that are not always formally analyzed statistically. The problem in the analysis of adverse events is their low incidence. Paucity of events causes serious problems in any statistical analysis (see Shuster et al28). The reason is that, with rare events, small changes in the data can cause dramatic changes in the results. This problem can persist even after pooling data from many studies. Instability of results is also exacerbated by the use of relative measures (eg, relative risk and odds ratio) instead of absolute measures of risk (eg, risk difference).
In a controversial meta-analysis, Nissen and Wolski4 combined 42 studies to examine the effect of rosiglitazone (Avandia) on the risk of myocardial infarction and death from cardiovascular causes. The overall estimated incidence of myocardial infarction in the treatment groups was 0.006 (86/14,376), or 6 in 1,000. Furthermore, 4 studies did not have any occurrences in either group, and 2 of the 42 studies accounted for 28.4% of the patients in the study.
Using a fixed-effect model, the odds ratio was 1.42, ie, the odds of myocardial infarction was 42% higher in patients using rosiglitazone, and the difference was statistically significant (95% confidence interval 1.03–1.98). Given the low frequency of myocardial infarction, this translates into an increase of only 1.78 myocardial infarctions per 1,000 patients (from 4.22 to 6 per 1,000). Furthermore, when the data were analyzed using other methods or if the two large studies were removed, the effect became nonsignificant.29 Nissen and Wolski’s study4 is valuable and raises an important issue. However, the medical community would have been better served if a sensitivity analysis had been presented to highlight the fragility of the conclusions.
META-ANALYSIS VS LARGE RANDOMIZED CONTROLLED TRIALS
There is debate about how meta-analyses compare with large randomized controlled trials. In situations where a meta-analysis and a subsequent large randomized controlled trial are available, discrepancies are not uncommon.
LeLorier et al6 compared the results of 19 meta-analyses and 12 subsequent large randomized controlled trials on the same topics. In 5 (12%) of the 40 outcomes studied, the results of the trials were significantly different than those of the meta-analysis. The authors mentioned publication bias, study heterogeneity, and differences in populations as plausible explanations for the disagreements. However, they correctly commented: “this does not appear to be a large percentage, since a divergence in 5 percent of cases would be expected on the basis of chance alone.”6
A key reason for discrepancies is that meta-analyses are based on heterogeneous, often small studies. The results of a meta-analysis can be generalized to a target population similar to the target population in each of the studies. The patients in the individual studies can be substantially different with respect to diagnostic criteria, comorbidities, severity of disease, geographic region, and the time when the trial was conducted, among other factors. On the other hand, even in a large randomized controlled trial, the target population is necessarily more limited. These differences can explain many of the disagreements in the results.
A large, well-designed, randomized controlled trial is considered the gold standard in the sense that it provides the most reliable information on the specific target population from which the sample was drawn. Within that population the results of a randomized controlled trial supersede those of a meta-analysis. However, a well conducted meta-analysis can provide complementary information that is valuable to a researcher, clinician, or policy-maker.
CONCLUSION
Like many other statistical techniques, meta-analysis is a powerful tool when used judiciously; however, there are many caveats in its application. Clearly, meta-analysis has an important role in medical research, public policy, and clinical practice. Its use and value will likely increase, given the amount of new knowledge, the speed at which it is being created, and the availability of specialized software for performing it.30 A meta-analysis needs to fulfill several key requirements to ensure the validity of its results:
- Well-defined objectives, including precise definitions of clinical variables and outcomes
- An appropriate and well-documented study identification and selection strategy
- Evaluation of bias in the identification and selection of studies
- Description and evaluation of heterogeneity
- Justification of data analytic techniques
- Use of sensitivity analysis.
It is imperative that researchers, policy-makers, and clinicians be able to critically assess the value and reliability of the conclusions of meta-analyses.
- Berlin JA, Colditz GA. The role of meta-analysis in the regulatory process for food, drugs, and devices. JAMA 1999; 281:830–834.
- Bailar JC. The promise and problems of meta-analysis. N Engl J Med 1997; 337:559–561.
- Simon R. Meta-analysis of clinical trials: opportunities and limitations. In: Stangl DK, Berry DA, editors. Meta-Analysis in Medicine and Health Policy. New York: Marcel Dekker, 2000.
- Nissen SE, Wolski K. Effect of rosiglitazone on the risk of myocardial infarction and death from cardiovascular causes. N Engl J Med 2007; 356:2457–2471.
- Turner EH, Matthews AM, Linardatos E, et al. Selective publication of antidepressant trials and its influence on apparent efficacy. N Engl J Med 2008; 358:252–260.
- LeLorier J, Grégoire G, Benhaddad A, Lapierre J, Derderian F. Discrepancies between meta-analyses and subsequent large randomized, controlled trials. N Engl J Med 1997; 337:536–542.
- Steinbrook R. Searching for the right search—reaching the medical literature. N Engl J Med 2006; 354:4–7.
- Dickersin K, Scherer R, Lefebvre C. Systematic reviews: identifying relevant studies for systematic reviews. BMJ 1994; 309:1286–1291.
- De Luca G, Suryapranta H, Stone GW, et al. Coronary stenting versus balloon angioplasty for acute myocardial infarction: a meta-regression analysis of randomized trials. Int J Cardiol 2007; 10.1016/j.ijcard.2007.03.112
- Ng TT, McGory ML, Ko CY, et al. Meta-analysis in surgery. Arch Surg 2006; 141:1125–1130.
- Ray CE, Prochazka A. The need for anticoagulation following inferior vena cava filter placement: systematic review. Cardiovasc Intervent Radiol 2007; 31:316–324.
- Nicolucci A, Grilli R, Alexanian AA, Apolone G, Torri V, Liberati A. Quality evolution and clinical implications of randomized controlled trials on the treatment of lung cancer. A lost opportunity for meta-analysis. JAMA 1989; 262:2101–2107.
- Marsoni S, Torri V, Taiana A. Critical review of the quality and development of randomized clinical trials and their influence on the treatment of advanced epithelial ovarian cancer. Ann Oncol 1990; 1:343–350.
- Moher D, Cook DJ, Eastwood S, Olkin I, Rennie D, Stroup DF. Improving the quality of reports of meta-analyses of randomised controlled trials: the QUOROM statement. Quality of Reporting of Meta-analyses. Lancet 1999; 354:1896–1900.
- Gami AS, Witt BJ, Howard DE, et al. Metabolic syndrome and risk of incident cardiovascular events and death. J Am Coll Cardiol 2007; 49:403–414.
- Terrin N, Schmid CH, Lau J, Olkin I. Adjusting for publication bias in the presence of heterogeneity. Stat Med 2003; 22:2113–2126.
- Dentali F, Doukelis D, Gianni M, et al. Meta-analysis: anticoagulant prophylaxis to prevent symptomatic venous thromboembolism in hospitalized medical patients. Ann Intern Med 2007; 146:278–288.
- Whitehead A. Meta-Analysis of Controlled Clinical Trials. New York: Wiley, 2002.
- Gebski V, Burmeister B, Smithers BM, et al. Survival benefits from neoadjuvant chemoradiotherapy or chemotherapy in oesophageal carcinoma: a meta-analysis. Lancet Oncology 2007; 8:226–234.
- Trivella M, Pezzella F, Pastorino U, et al. Microvessel density as a prognostic factor in non-small-cell lung carcinoma: a meta-analysis of individual patient data. Lancet Oncology 2007; 8:488–499.
- Kunz R, Vist G, Oxman AD. Randomisation to protect against selection bias in healthcare trials (Cochrane Methodology Review). The Cochrane Library, 1, 2003. Oxford: Update Software.
- Gillum LA, Mamidipudi SK, Johnston SC. Ischemic stroke risk with oral contraceptives: a meta-analysis. JAMA 2000; 284:72–78.
- Chan WS, Ray J, Wai EK, et al. Risk of stroke in women exposed to low-dose oral contraceptives. Arch Intern Med 2004; 164:741–747.
- Gillum LA, Johnston SC. Oral contraceptives and stroke risk: the debate continues. Lancet 2004; 3:453–454.
- Bhutta AT, Cleves MA, Casey PH, et al. Cognitive and behavioral outcomes of school–aged children who were born preterm. JAMA 2002; 288:728–737.
- De Luca G, Suryapranta H, Stone GW, et al. Adjunctive mechanical devices to prevent distal embolization in patients undergoing mechanical revascularization for acute myocardial infarction: a meta-analysis of randomized trials. Am Heart J 2007; 153:343–353.
- Wang R, Lagakos SW, Ware JH, et al. Statistics in medicine—reporting of subgroup analyses in clinical trials. N Engl J Med 2007; 357:2189–2194.
- Shuster JJ, Jones LS, Salmon DA. Fixed vs random effects meta-analysis in rare events: the rosiglitazone link with myocardial infarction and cardiac death. Stat Med 2007; 26:4375–4385.
- Bracken MB. Rosiglitazone and cardiovascular risk. N Engl J Med 2007; 357:937–938.
- Sutton AJ, Lambert PC, Hellmich M, et al. Meta-analysis in practice: a critical review of available software. In:Stangl DK, Berry DA, editors. Meta-Analysis in Medicine and Health Policy. New York: Marcel Dekker, 2000.
The amount of information generated in medical research is becoming overwhelming, even for experienced researchers. New studies are constantly being published, and clinicians are finding it nearly impossible to stay current, even in their own area of specialty.
To help make sense of the information, we are seeing more and more review articles that pool the results of multiple studies. When certain principles are followed and the data are quantitatively analyzed, these reviews are called meta-analyses. A PubMed search of the word “meta-analysis” in the title yielded 1,473 articles in the year 2007.
Combining available information to generate an integrated result seems reasonable and can save a considerable amount of resources. Nowadays, meta-analyses are being used to design future research, to provide evidence in the regulatory process,1 and even to modify clinical practice.
Meta-analysis is powerful but also controversial—controversial because several conditions are critical to a sound meta-analysis, and small violations of those conditions can lead to misleading results. Summarizing large amounts of varied information using a single number is another controversial aspect of meta-analysis. Under scrutiny, some meta-analyses have been inappropriate, and their conclusions not fully warranted.2,3
This article introduces the basic concepts of meta-analysis and discusses its caveats, with the aim of helping clinicians assess the merits of the results. We will use several recent meta-analyses to illustrate the issues, including a controversial one4 with potentially far-reaching consequences.
OBJECTIVES OF META-ANALYSIS
The main objectives of a meta-analysis are to:
- Summarize and integrate results from a number of individual studies
- Analyze differences in the results among studies
- Overcome small sample sizes of individual studies to detect effects of interest, and analyze end points that require larger sample sizes
- Increase precision in estimating effects
- Evaluate effects in subsets of patients
- Determine if new studies are needed to further investigate an issue
- Generate new hypotheses for future studies.
These lofty objectives can only be achieved when the meta-analysis satisfactorily addresses certain critical issues, which we will discuss next.
CRITICAL ISSUES IN META-ANALYSIS DESIGN
Four critical issues need to be addressed in a meta-analysis:
- Identification and selection of studies
- Heterogeneity of results
- Availability of information
- Analysis of the data.
IDENTIFICATION AND SELECTION OF STUDIES
The outcome of a meta-analysis depends on the studies included. The critical aspect of selecting studies to be included in a meta-analysis consists of two phases. The first is the identification phase or literature search, in which potential studies are identified. In the second phase, further criteria are used to create a list of studies for inclusion. Three insidious problems plague this aspect of meta-analysis: publication bias and search bias in the identification phase, and selection bias in the selection phase. These biases are discussed below.
Publication bias: ‘Positive’ studies are more likely to be printed
Searches of databases such as PubMed or Embase can yield long lists of studies. However, these databases include only studies that have been published. Such searches are unlikely to yield a representative sample because studies that show a “positive” result (usually in favor of a new treatment or against a well-established one) are more likely to be published than those that do not. This selective publication of studies is called publication bias.
In a recent article, Turner et al5 analyzed the publication status of studies of antidepressants. Based on studies registered with the US Food and Drug Administration (FDA), they found that 97% of the positive studies were published vs only 12% of the negative ones. Furthermore, when the nonpublished studies were not included in the analysis, the positive effects of individual drugs increased between 11% and 69%.
One reason for publication bias is that drug manufacturers are not generally interested in publishing negative studies. Another may be that editors favor positive studies because these are the ones that make the headlines and give the publication visibility. In some medical areas, the exclusion of studies conducted in non-English-speaking countries can increase publication bias.6
To ameliorate the effect of publication bias on the results of a meta-analysis, a serious effort should be made to identify unpublished studies. Identifying unpublished studies is easier now, thanks to improved communication between researchers worldwide, and thanks to registries in which all the studies of a certain disease or treatment are reported regardless of the result.
The National Institutes of Health maintains a registry of all the studies it supports, and the FDA keeps a registry and database in which drug companies must register all trials they intend to use in applying for marketing approval or a change in labeling. “Banks” of published and unpublished trials supported by pharmaceutical companies are also available (eg, http://ctr.gsk.co.uk/welcome.asp). The Cochrane collaboration (www.cochrane.org/) keeps records of systematic reviews and meta-analyses of many diseases and procedures.
Search bias: Identifying relevant studies
Even in the ideal case that all relevant studies were available (ie, no publication bias), a faulty search can miss some of them. In searching databases, much care should be taken to assure that the set of key words used for searching is as complete as possible. This step is so critical that most recent meta-analyses include the list of key words used. The search engine (eg, PubMed, Google) is also critical, affecting the type and number of studies that are found.7 Small differences in search strategies can produce large differences in the set of studies found.8
Selection bias: Choosing the studies to be included
The identification phase usually yields a long list of potential studies, many of which are not directly relevant to the topic of the meta-analysis. This list is then subject to additional criteria to select the studies to be included. This critical step is also designed to reduce differences among studies, eliminate replication of data or studies, and improve data quality, and thus enhance the validity of the results.
To reduce the possibility of selection bias in this phase, it is crucial for the criteria to be clearly defined and for the studies to be scored by more than one researcher, with the final list chosen by consensus.9,10 Frequently used criteria in this phase are in the areas of:
- Objectives
- Populations studied
- Study design (eg, experimental vs observational)
- Sample size
- Treatment (eg, type and dosage)
- Criteria for selection of controls
- Outcomes measured
- Quality of the data
- Analysis and reporting of results
- Accounting and reporting of attrition rates
- Length of follow-up
- When the study was conducted.
The objective in this phase is to select studies that are as similar as possible with respect to these criteria. It is a fact that even with careful selection, differences among studies will remain. But when the dissimilarities are large it becomes hard to justify pooling the results to obtain a “unified” conclusion.
In some cases, it is particularly difficult to find similar studies,10,11 and sometimes the discrepancies and low quality of the studies can prevent a reasonable integration of results. In a systematic review of advanced lung cancer, Nicolucci et al12 decided not to pool the results, in view of “systematic qualitative inadequacy of almost all trials” and lack of consistency in the studies and their methods. Marsoni et al13 came to a similar conclusion in attempting to summarize results in advanced ovarian cancer.
Stratification is an effective way to deal with inherent differences among studies and to improve the quality and usefulness of the conclusions. An added advantage to stratification is that insight can be gained by investigating discrepancies among strata.
There are many ways to create coherent subgroups of studies. For example, studies can be stratified according to their “quality,” assigned by certain scoring systems. Commonly used systems award points on the basis of how patients were selected and randomized, the type of blinding, the dropout rate, the outcome measurement, and the type of analysis (eg, intention-to-treat). However, these criteria, and therefore the scores, are somewhat subjective. Moher et al14 expand on this issue.
Large differences in sample sizes among studies are not uncommon and can cause problems in the analysis. Depending on the type of model used (see below), meta-analyses combine results based on the size of each study, but when the studies vary significantly in size, the large studies can still have an unduly large influence on the results. Stratifying by sample size is done sometimes to verify the stability of the results.4
On the other hand, the presence of dissimilarities among studies can have advantages by increasing the generalizability of the conclusions. Berlin and Colditz1 point out that “we gain strength in inference when the range of patient characteristics has been broadened by replicating findings in studies with populations that vary in age range, geographic region, severity of underlying illness, and the like.”
Funnel plot: Detecting biases in the identification and selection of studies
The funnel plot is a technique used to investigate the possibility of biases in the identification and selection phases. In a funnel plot the size of the effect (defined as a measure of the difference between treatment and control) in each study is plotted on the horizontal axis against standard error15 or sample size9 on the vertical axis. If there are no biases, the graph will tend to have a symmetrical funnel shape centered in the average effect of the studies. When negative studies are missing, the graph shows lack of symmetry.
Funnel plots are appealing because they are simple, but their objective is to detect a complex effect, and they can be misleading. For example, lack of symmetry in a funnel plot can also be caused by heterogeneity in the studies.16 Another problem with funnel plots is that they are difficult to interpret when the number of studies is small. In some cases, however, the researcher may not have any option but to perform the analysis and report the presence of bias.11
HETEROGENEITY OF RESULTS
In meta-analysis, heterogeneity refers to the degree of dissimilarity in the results of individual studies. In some cases, the dissimilarities in results can be traced back to inherent differences in the individual studies. In other situations, however, causes for the dissimilarities might not be easy to elucidate. In any case, as the level of heterogeneity increases, the justification for an integrated result becomes more difficult. A tool that is very effective to display the level of heterogeneity is the forest plot. In a forest plot, the estimated effect of each study along with a line representing a confidence interval is drawn. When the effects are similar, the confidence intervals overlap, and heterogeneity is low. The forest plot includes a reference line at the point of no effect (eg, one for relative risks and odds ratios). When some effects lie on opposite sides of the reference line, it means that the studies are contradictory and heterogeneity is high. In such cases, the conclusions of a meta-analysis are compromised.
AVAILABILITY OF INFORMATION
Most reports of individual studies include only summary results, such as means, standard deviations, proportions, odds ratios, and relative risks. Other than the possibility of errors in reporting, the lack of information can severely limit the type of analyses and conclusions that can be reached in a meta-analysis. For example, lack of information from individual studies can preclude the comparison of effects in predetermined subgroups of patients.
The best scenario is when data at the patient level are available. In such cases, the researcher has great flexibility in the analysis of the information. Trivella et al20 performed a meta-analysis of the value of microvessel density in predicting survival in non-small-cell lung cancer. They obtained information on individual patients by contacting research centers directly. The data allowed them to vary the cutoff point to classify microvessel density as high or low and to use statistical methods to ameliorate heterogeneity.
A frequent problem in meta-analysis is the lack of uniformity in how outcomes are measured. In the study by Trivella et al,20 the microvessel density was measured by two methods. The microvessel density was a significant prognostic factor when measured by one of the methods, but not the other.
RANDOMIZED CONTROLLED TRIALS VS OBSERVATIONAL STUDIES
Some researchers believe that meta-analyses should be conducted only on randomized controlled trials.3,21 Their reasoning is that meta-analyses should include only reasonably well-conducted studies to reduce the risk of a misleading conclusion. However, many important diseases can only be studied observationally. If these studies have a certain level of quality, there is no technical reason not to include them in a meta-analysis.
Gillum et al22 performed a meta-analysis published in 2000 on the risk of ischemic stroke in users of oral contraceptives, based on observational studies (since no randomized trials were available). Studies were identified and selected by multiple researchers using strict criteria to make sure that only studies fulfilling certain standards were included. Of 804 potentially relevant studies identified, only 16 were included in the final analysis. A funnel plot showed no evidence of bias and the level of heterogeneity was fairly low. The meta-analysis result confirmed the results of individual studies, but the precision with which the effect was estimated was much higher. The overall relative risk of stroke in women taking oral contraceptives was 2.75, with a 95% confidence interval of 2.24 to 3.38.
A more recent meta-analysis23 (published in 2004) on the same issue found no significant increase in the risk of ischemic stroke with the use of oral contraceptives. Gillum and Johnston24 suggest that the main reason for the discrepancy is the lower amount of estrogen in newer oral contraceptives. They also point out differences in the control groups and study outcomes as reasons for the discrepancies between the two studies.
Bhutta et al25 performed a meta-analysis of case-control (observational) studies of the effect of preterm birth on cognitive and behavioral outcomes. Studies were included only if the children were evaluated after their fifth birthday and the attrition rate was less than 30%. The studies were grouped according to criteria of quality devised specifically for case-control studies. The high-quality studies tended to show a larger effect than the low-quality studies, but the difference was not significant. Seventeen studies were included, and all of them found that children born preterm had lower cognitive scores; the difference was statistically significant in 15 of the studies. As expected, the meta-analysis confirmed these findings (95% confidence interval for the difference 9.2–12.5). The number of patients (1,556 cases and 1,720 controls) in the meta-analysis allowed the researchers to conclude further that the mean cognitive scores were directly proportional to the mean birth weight (R2 = 0.51, P < .001) and gestational age (R2 = 0.49, P < .001).
ANALYSIS OF DATA
There are specific statistical techniques that are used in meta-analysis to analyze and integrate the information. The data from the individual studies can be analyzed using either of two models: fixed effects or random effects.
The fixed-effects model assumes that the treatment effect is the same across studies. This common effect is unknown, and the purpose of the analysis is to estimate it with more precision than in the individual studies.
The random-effects model, on the other hand, assumes that the treatment effect is not the same across studies. The goal is to estimate the average effect in the studies.
In the fixed-effects model, the results of individual studies are pooled using weights that depend on the sample size of the study, whereas in the random-effects model each study is weighted equally. Due to the heterogeneity among studies, the random-effects model yields wider confidence intervals.
Both models have pros and cons. In many cases, the assumption that the treatment effect is the same in all the studies is not tenable, and the random-effects model is preferable. When the effect of interest is large, the results of both models tend to agree, particularly when the studies are balanced (ie, they have a similar number of patients in the treatment group as in the control group) and the study sizes are similar. But when the effect is small or when the level of heterogeneity of the studies is high, the result of the meta-analysis is likely to depend on the model used. In those cases, the analysis should be done and presented using both models.
It is highly desirable for a meta-analysis to include a sensitivity analysis to determine the “robustness” of the results. Two common ways to perform sensitivity analysis are to analyze the data using various methods and to present the results when some studies are removed from the analysis.26 If these actions cause serious changes in the overall results, the credibility of the results is compromised.
The strength of meta-analysis is that, by pooling many studies, the effective sample size is greatly increased, and consequently more variables and outcomes can be examined. For example, analysis in subsets of patients and regression analyses9 that could not be done in individual trials can be performed in a meta-analysis.
A word of caution should be given with respect to larger samples and the possibility of multiple analyses of the data in meta-analysis. Much care must be exercised when examining the significance of effects that are not considered prior to the meta-analysis. The testing of effects suggested by the data and not planned a priori (sometimes called “data-mining”) increases considerably the risk of false-positive results. One common problem with large samples is the temptation to perform many so-called “subgroup analyses” in which subgroups of patients formed according to multiple baseline characteristics are compared.27 The best way to minimize the possibility of false-positive results is to determine the effects to be tested before the data are collected and analyzed. Another method is to adjust the P value according to the number of analyses performed. In general, post hoc analyses should be deemed exploratory, and the reader should be made aware of this fact in order to judge the validity of the conclusion.
META-ANALYSIS OF RARE EVENTS
Lately, meta-analysis has been used to analyze outcomes that are rare and that individual studies were not designed to test. In general, the sample size of individual studies provides inadequate power to test rare outcomes. Adverse events are prime examples of important rare outcomes that are not always formally analyzed statistically. The problem in the analysis of adverse events is their low incidence. Paucity of events causes serious problems in any statistical analysis (see Shuster et al28). The reason is that, with rare events, small changes in the data can cause dramatic changes in the results. This problem can persist even after pooling data from many studies. Instability of results is also exacerbated by the use of relative measures (eg, relative risk and odds ratio) instead of absolute measures of risk (eg, risk difference).
In a controversial meta-analysis, Nissen and Wolski4 combined 42 studies to examine the effect of rosiglitazone (Avandia) on the risk of myocardial infarction and death from cardiovascular causes. The overall estimated incidence of myocardial infarction in the treatment groups was 0.006 (86/14,376), or 6 in 1,000. Furthermore, 4 studies did not have any occurrences in either group, and 2 of the 42 studies accounted for 28.4% of the patients in the study.
Using a fixed-effect model, the odds ratio was 1.42, ie, the odds of myocardial infarction was 42% higher in patients using rosiglitazone, and the difference was statistically significant (95% confidence interval 1.03–1.98). Given the low frequency of myocardial infarction, this translates into an increase of only 1.78 myocardial infarctions per 1,000 patients (from 4.22 to 6 per 1,000). Furthermore, when the data were analyzed using other methods or if the two large studies were removed, the effect became nonsignificant.29 Nissen and Wolski’s study4 is valuable and raises an important issue. However, the medical community would have been better served if a sensitivity analysis had been presented to highlight the fragility of the conclusions.
META-ANALYSIS VS LARGE RANDOMIZED CONTROLLED TRIALS
There is debate about how meta-analyses compare with large randomized controlled trials. In situations where a meta-analysis and a subsequent large randomized controlled trial are available, discrepancies are not uncommon.
LeLorier et al6 compared the results of 19 meta-analyses and 12 subsequent large randomized controlled trials on the same topics. In 5 (12%) of the 40 outcomes studied, the results of the trials were significantly different than those of the meta-analysis. The authors mentioned publication bias, study heterogeneity, and differences in populations as plausible explanations for the disagreements. However, they correctly commented: “this does not appear to be a large percentage, since a divergence in 5 percent of cases would be expected on the basis of chance alone.”6
A key reason for discrepancies is that meta-analyses are based on heterogeneous, often small studies. The results of a meta-analysis can be generalized to a target population similar to the target population in each of the studies. The patients in the individual studies can be substantially different with respect to diagnostic criteria, comorbidities, severity of disease, geographic region, and the time when the trial was conducted, among other factors. On the other hand, even in a large randomized controlled trial, the target population is necessarily more limited. These differences can explain many of the disagreements in the results.
A large, well-designed, randomized controlled trial is considered the gold standard in the sense that it provides the most reliable information on the specific target population from which the sample was drawn. Within that population the results of a randomized controlled trial supersede those of a meta-analysis. However, a well conducted meta-analysis can provide complementary information that is valuable to a researcher, clinician, or policy-maker.
CONCLUSION
Like many other statistical techniques, meta-analysis is a powerful tool when used judiciously; however, there are many caveats in its application. Clearly, meta-analysis has an important role in medical research, public policy, and clinical practice. Its use and value will likely increase, given the amount of new knowledge, the speed at which it is being created, and the availability of specialized software for performing it.30 A meta-analysis needs to fulfill several key requirements to ensure the validity of its results:
- Well-defined objectives, including precise definitions of clinical variables and outcomes
- An appropriate and well-documented study identification and selection strategy
- Evaluation of bias in the identification and selection of studies
- Description and evaluation of heterogeneity
- Justification of data analytic techniques
- Use of sensitivity analysis.
It is imperative that researchers, policy-makers, and clinicians be able to critically assess the value and reliability of the conclusions of meta-analyses.
The amount of information generated in medical research is becoming overwhelming, even for experienced researchers. New studies are constantly being published, and clinicians are finding it nearly impossible to stay current, even in their own area of specialty.
To help make sense of the information, we are seeing more and more review articles that pool the results of multiple studies. When certain principles are followed and the data are quantitatively analyzed, these reviews are called meta-analyses. A PubMed search of the word “meta-analysis” in the title yielded 1,473 articles in the year 2007.
Combining available information to generate an integrated result seems reasonable and can save a considerable amount of resources. Nowadays, meta-analyses are being used to design future research, to provide evidence in the regulatory process,1 and even to modify clinical practice.
Meta-analysis is powerful but also controversial—controversial because several conditions are critical to a sound meta-analysis, and small violations of those conditions can lead to misleading results. Summarizing large amounts of varied information using a single number is another controversial aspect of meta-analysis. Under scrutiny, some meta-analyses have been inappropriate, and their conclusions not fully warranted.2,3
This article introduces the basic concepts of meta-analysis and discusses its caveats, with the aim of helping clinicians assess the merits of the results. We will use several recent meta-analyses to illustrate the issues, including a controversial one4 with potentially far-reaching consequences.
OBJECTIVES OF META-ANALYSIS
The main objectives of a meta-analysis are to:
- Summarize and integrate results from a number of individual studies
- Analyze differences in the results among studies
- Overcome small sample sizes of individual studies to detect effects of interest, and analyze end points that require larger sample sizes
- Increase precision in estimating effects
- Evaluate effects in subsets of patients
- Determine if new studies are needed to further investigate an issue
- Generate new hypotheses for future studies.
These lofty objectives can only be achieved when the meta-analysis satisfactorily addresses certain critical issues, which we will discuss next.
CRITICAL ISSUES IN META-ANALYSIS DESIGN
Four critical issues need to be addressed in a meta-analysis:
- Identification and selection of studies
- Heterogeneity of results
- Availability of information
- Analysis of the data.
IDENTIFICATION AND SELECTION OF STUDIES
The outcome of a meta-analysis depends on the studies included. The critical aspect of selecting studies to be included in a meta-analysis consists of two phases. The first is the identification phase or literature search, in which potential studies are identified. In the second phase, further criteria are used to create a list of studies for inclusion. Three insidious problems plague this aspect of meta-analysis: publication bias and search bias in the identification phase, and selection bias in the selection phase. These biases are discussed below.
Publication bias: ‘Positive’ studies are more likely to be printed
Searches of databases such as PubMed or Embase can yield long lists of studies. However, these databases include only studies that have been published. Such searches are unlikely to yield a representative sample because studies that show a “positive” result (usually in favor of a new treatment or against a well-established one) are more likely to be published than those that do not. This selective publication of studies is called publication bias.
In a recent article, Turner et al5 analyzed the publication status of studies of antidepressants. Based on studies registered with the US Food and Drug Administration (FDA), they found that 97% of the positive studies were published vs only 12% of the negative ones. Furthermore, when the nonpublished studies were not included in the analysis, the positive effects of individual drugs increased between 11% and 69%.
One reason for publication bias is that drug manufacturers are not generally interested in publishing negative studies. Another may be that editors favor positive studies because these are the ones that make the headlines and give the publication visibility. In some medical areas, the exclusion of studies conducted in non-English-speaking countries can increase publication bias.6
To ameliorate the effect of publication bias on the results of a meta-analysis, a serious effort should be made to identify unpublished studies. Identifying unpublished studies is easier now, thanks to improved communication between researchers worldwide, and thanks to registries in which all the studies of a certain disease or treatment are reported regardless of the result.
The National Institutes of Health maintains a registry of all the studies it supports, and the FDA keeps a registry and database in which drug companies must register all trials they intend to use in applying for marketing approval or a change in labeling. “Banks” of published and unpublished trials supported by pharmaceutical companies are also available (eg, http://ctr.gsk.co.uk/welcome.asp). The Cochrane collaboration (www.cochrane.org/) keeps records of systematic reviews and meta-analyses of many diseases and procedures.
Search bias: Identifying relevant studies
Even in the ideal case that all relevant studies were available (ie, no publication bias), a faulty search can miss some of them. In searching databases, much care should be taken to assure that the set of key words used for searching is as complete as possible. This step is so critical that most recent meta-analyses include the list of key words used. The search engine (eg, PubMed, Google) is also critical, affecting the type and number of studies that are found.7 Small differences in search strategies can produce large differences in the set of studies found.8
Selection bias: Choosing the studies to be included
The identification phase usually yields a long list of potential studies, many of which are not directly relevant to the topic of the meta-analysis. This list is then subject to additional criteria to select the studies to be included. This critical step is also designed to reduce differences among studies, eliminate replication of data or studies, and improve data quality, and thus enhance the validity of the results.
To reduce the possibility of selection bias in this phase, it is crucial for the criteria to be clearly defined and for the studies to be scored by more than one researcher, with the final list chosen by consensus.9,10 Frequently used criteria in this phase are in the areas of:
- Objectives
- Populations studied
- Study design (eg, experimental vs observational)
- Sample size
- Treatment (eg, type and dosage)
- Criteria for selection of controls
- Outcomes measured
- Quality of the data
- Analysis and reporting of results
- Accounting and reporting of attrition rates
- Length of follow-up
- When the study was conducted.
The objective in this phase is to select studies that are as similar as possible with respect to these criteria. It is a fact that even with careful selection, differences among studies will remain. But when the dissimilarities are large it becomes hard to justify pooling the results to obtain a “unified” conclusion.
In some cases, it is particularly difficult to find similar studies,10,11 and sometimes the discrepancies and low quality of the studies can prevent a reasonable integration of results. In a systematic review of advanced lung cancer, Nicolucci et al12 decided not to pool the results, in view of “systematic qualitative inadequacy of almost all trials” and lack of consistency in the studies and their methods. Marsoni et al13 came to a similar conclusion in attempting to summarize results in advanced ovarian cancer.
Stratification is an effective way to deal with inherent differences among studies and to improve the quality and usefulness of the conclusions. An added advantage to stratification is that insight can be gained by investigating discrepancies among strata.
There are many ways to create coherent subgroups of studies. For example, studies can be stratified according to their “quality,” assigned by certain scoring systems. Commonly used systems award points on the basis of how patients were selected and randomized, the type of blinding, the dropout rate, the outcome measurement, and the type of analysis (eg, intention-to-treat). However, these criteria, and therefore the scores, are somewhat subjective. Moher et al14 expand on this issue.
Large differences in sample sizes among studies are not uncommon and can cause problems in the analysis. Depending on the type of model used (see below), meta-analyses combine results based on the size of each study, but when the studies vary significantly in size, the large studies can still have an unduly large influence on the results. Stratifying by sample size is done sometimes to verify the stability of the results.4
On the other hand, the presence of dissimilarities among studies can have advantages by increasing the generalizability of the conclusions. Berlin and Colditz1 point out that “we gain strength in inference when the range of patient characteristics has been broadened by replicating findings in studies with populations that vary in age range, geographic region, severity of underlying illness, and the like.”
Funnel plot: Detecting biases in the identification and selection of studies
The funnel plot is a technique used to investigate the possibility of biases in the identification and selection phases. In a funnel plot the size of the effect (defined as a measure of the difference between treatment and control) in each study is plotted on the horizontal axis against standard error15 or sample size9 on the vertical axis. If there are no biases, the graph will tend to have a symmetrical funnel shape centered in the average effect of the studies. When negative studies are missing, the graph shows lack of symmetry.
Funnel plots are appealing because they are simple, but their objective is to detect a complex effect, and they can be misleading. For example, lack of symmetry in a funnel plot can also be caused by heterogeneity in the studies.16 Another problem with funnel plots is that they are difficult to interpret when the number of studies is small. In some cases, however, the researcher may not have any option but to perform the analysis and report the presence of bias.11
HETEROGENEITY OF RESULTS
In meta-analysis, heterogeneity refers to the degree of dissimilarity in the results of individual studies. In some cases, the dissimilarities in results can be traced back to inherent differences in the individual studies. In other situations, however, causes for the dissimilarities might not be easy to elucidate. In any case, as the level of heterogeneity increases, the justification for an integrated result becomes more difficult. A tool that is very effective to display the level of heterogeneity is the forest plot. In a forest plot, the estimated effect of each study along with a line representing a confidence interval is drawn. When the effects are similar, the confidence intervals overlap, and heterogeneity is low. The forest plot includes a reference line at the point of no effect (eg, one for relative risks and odds ratios). When some effects lie on opposite sides of the reference line, it means that the studies are contradictory and heterogeneity is high. In such cases, the conclusions of a meta-analysis are compromised.
AVAILABILITY OF INFORMATION
Most reports of individual studies include only summary results, such as means, standard deviations, proportions, odds ratios, and relative risks. Other than the possibility of errors in reporting, the lack of information can severely limit the type of analyses and conclusions that can be reached in a meta-analysis. For example, lack of information from individual studies can preclude the comparison of effects in predetermined subgroups of patients.
The best scenario is when data at the patient level are available. In such cases, the researcher has great flexibility in the analysis of the information. Trivella et al20 performed a meta-analysis of the value of microvessel density in predicting survival in non-small-cell lung cancer. They obtained information on individual patients by contacting research centers directly. The data allowed them to vary the cutoff point to classify microvessel density as high or low and to use statistical methods to ameliorate heterogeneity.
A frequent problem in meta-analysis is the lack of uniformity in how outcomes are measured. In the study by Trivella et al,20 the microvessel density was measured by two methods. The microvessel density was a significant prognostic factor when measured by one of the methods, but not the other.
RANDOMIZED CONTROLLED TRIALS VS OBSERVATIONAL STUDIES
Some researchers believe that meta-analyses should be conducted only on randomized controlled trials.3,21 Their reasoning is that meta-analyses should include only reasonably well-conducted studies to reduce the risk of a misleading conclusion. However, many important diseases can only be studied observationally. If these studies have a certain level of quality, there is no technical reason not to include them in a meta-analysis.
Gillum et al22 performed a meta-analysis published in 2000 on the risk of ischemic stroke in users of oral contraceptives, based on observational studies (since no randomized trials were available). Studies were identified and selected by multiple researchers using strict criteria to make sure that only studies fulfilling certain standards were included. Of 804 potentially relevant studies identified, only 16 were included in the final analysis. A funnel plot showed no evidence of bias and the level of heterogeneity was fairly low. The meta-analysis result confirmed the results of individual studies, but the precision with which the effect was estimated was much higher. The overall relative risk of stroke in women taking oral contraceptives was 2.75, with a 95% confidence interval of 2.24 to 3.38.
A more recent meta-analysis23 (published in 2004) on the same issue found no significant increase in the risk of ischemic stroke with the use of oral contraceptives. Gillum and Johnston24 suggest that the main reason for the discrepancy is the lower amount of estrogen in newer oral contraceptives. They also point out differences in the control groups and study outcomes as reasons for the discrepancies between the two studies.
Bhutta et al25 performed a meta-analysis of case-control (observational) studies of the effect of preterm birth on cognitive and behavioral outcomes. Studies were included only if the children were evaluated after their fifth birthday and the attrition rate was less than 30%. The studies were grouped according to criteria of quality devised specifically for case-control studies. The high-quality studies tended to show a larger effect than the low-quality studies, but the difference was not significant. Seventeen studies were included, and all of them found that children born preterm had lower cognitive scores; the difference was statistically significant in 15 of the studies. As expected, the meta-analysis confirmed these findings (95% confidence interval for the difference 9.2–12.5). The number of patients (1,556 cases and 1,720 controls) in the meta-analysis allowed the researchers to conclude further that the mean cognitive scores were directly proportional to the mean birth weight (R2 = 0.51, P < .001) and gestational age (R2 = 0.49, P < .001).
ANALYSIS OF DATA
There are specific statistical techniques that are used in meta-analysis to analyze and integrate the information. The data from the individual studies can be analyzed using either of two models: fixed effects or random effects.
The fixed-effects model assumes that the treatment effect is the same across studies. This common effect is unknown, and the purpose of the analysis is to estimate it with more precision than in the individual studies.
The random-effects model, on the other hand, assumes that the treatment effect is not the same across studies. The goal is to estimate the average effect in the studies.
In the fixed-effects model, the results of individual studies are pooled using weights that depend on the sample size of the study, whereas in the random-effects model each study is weighted equally. Due to the heterogeneity among studies, the random-effects model yields wider confidence intervals.
Both models have pros and cons. In many cases, the assumption that the treatment effect is the same in all the studies is not tenable, and the random-effects model is preferable. When the effect of interest is large, the results of both models tend to agree, particularly when the studies are balanced (ie, they have a similar number of patients in the treatment group as in the control group) and the study sizes are similar. But when the effect is small or when the level of heterogeneity of the studies is high, the result of the meta-analysis is likely to depend on the model used. In those cases, the analysis should be done and presented using both models.
It is highly desirable for a meta-analysis to include a sensitivity analysis to determine the “robustness” of the results. Two common ways to perform sensitivity analysis are to analyze the data using various methods and to present the results when some studies are removed from the analysis.26 If these actions cause serious changes in the overall results, the credibility of the results is compromised.
The strength of meta-analysis is that, by pooling many studies, the effective sample size is greatly increased, and consequently more variables and outcomes can be examined. For example, analysis in subsets of patients and regression analyses9 that could not be done in individual trials can be performed in a meta-analysis.
A word of caution should be given with respect to larger samples and the possibility of multiple analyses of the data in meta-analysis. Much care must be exercised when examining the significance of effects that are not considered prior to the meta-analysis. The testing of effects suggested by the data and not planned a priori (sometimes called “data-mining”) increases considerably the risk of false-positive results. One common problem with large samples is the temptation to perform many so-called “subgroup analyses” in which subgroups of patients formed according to multiple baseline characteristics are compared.27 The best way to minimize the possibility of false-positive results is to determine the effects to be tested before the data are collected and analyzed. Another method is to adjust the P value according to the number of analyses performed. In general, post hoc analyses should be deemed exploratory, and the reader should be made aware of this fact in order to judge the validity of the conclusion.
META-ANALYSIS OF RARE EVENTS
Lately, meta-analysis has been used to analyze outcomes that are rare and that individual studies were not designed to test. In general, the sample size of individual studies provides inadequate power to test rare outcomes. Adverse events are prime examples of important rare outcomes that are not always formally analyzed statistically. The problem in the analysis of adverse events is their low incidence. Paucity of events causes serious problems in any statistical analysis (see Shuster et al28). The reason is that, with rare events, small changes in the data can cause dramatic changes in the results. This problem can persist even after pooling data from many studies. Instability of results is also exacerbated by the use of relative measures (eg, relative risk and odds ratio) instead of absolute measures of risk (eg, risk difference).
In a controversial meta-analysis, Nissen and Wolski4 combined 42 studies to examine the effect of rosiglitazone (Avandia) on the risk of myocardial infarction and death from cardiovascular causes. The overall estimated incidence of myocardial infarction in the treatment groups was 0.006 (86/14,376), or 6 in 1,000. Furthermore, 4 studies did not have any occurrences in either group, and 2 of the 42 studies accounted for 28.4% of the patients in the study.
Using a fixed-effect model, the odds ratio was 1.42, ie, the odds of myocardial infarction was 42% higher in patients using rosiglitazone, and the difference was statistically significant (95% confidence interval 1.03–1.98). Given the low frequency of myocardial infarction, this translates into an increase of only 1.78 myocardial infarctions per 1,000 patients (from 4.22 to 6 per 1,000). Furthermore, when the data were analyzed using other methods or if the two large studies were removed, the effect became nonsignificant.29 Nissen and Wolski’s study4 is valuable and raises an important issue. However, the medical community would have been better served if a sensitivity analysis had been presented to highlight the fragility of the conclusions.
META-ANALYSIS VS LARGE RANDOMIZED CONTROLLED TRIALS
There is debate about how meta-analyses compare with large randomized controlled trials. In situations where a meta-analysis and a subsequent large randomized controlled trial are available, discrepancies are not uncommon.
LeLorier et al6 compared the results of 19 meta-analyses and 12 subsequent large randomized controlled trials on the same topics. In 5 (12%) of the 40 outcomes studied, the results of the trials were significantly different than those of the meta-analysis. The authors mentioned publication bias, study heterogeneity, and differences in populations as plausible explanations for the disagreements. However, they correctly commented: “this does not appear to be a large percentage, since a divergence in 5 percent of cases would be expected on the basis of chance alone.”6
A key reason for discrepancies is that meta-analyses are based on heterogeneous, often small studies. The results of a meta-analysis can be generalized to a target population similar to the target population in each of the studies. The patients in the individual studies can be substantially different with respect to diagnostic criteria, comorbidities, severity of disease, geographic region, and the time when the trial was conducted, among other factors. On the other hand, even in a large randomized controlled trial, the target population is necessarily more limited. These differences can explain many of the disagreements in the results.
A large, well-designed, randomized controlled trial is considered the gold standard in the sense that it provides the most reliable information on the specific target population from which the sample was drawn. Within that population the results of a randomized controlled trial supersede those of a meta-analysis. However, a well conducted meta-analysis can provide complementary information that is valuable to a researcher, clinician, or policy-maker.
CONCLUSION
Like many other statistical techniques, meta-analysis is a powerful tool when used judiciously; however, there are many caveats in its application. Clearly, meta-analysis has an important role in medical research, public policy, and clinical practice. Its use and value will likely increase, given the amount of new knowledge, the speed at which it is being created, and the availability of specialized software for performing it.30 A meta-analysis needs to fulfill several key requirements to ensure the validity of its results:
- Well-defined objectives, including precise definitions of clinical variables and outcomes
- An appropriate and well-documented study identification and selection strategy
- Evaluation of bias in the identification and selection of studies
- Description and evaluation of heterogeneity
- Justification of data analytic techniques
- Use of sensitivity analysis.
It is imperative that researchers, policy-makers, and clinicians be able to critically assess the value and reliability of the conclusions of meta-analyses.
- Berlin JA, Colditz GA. The role of meta-analysis in the regulatory process for food, drugs, and devices. JAMA 1999; 281:830–834.
- Bailar JC. The promise and problems of meta-analysis. N Engl J Med 1997; 337:559–561.
- Simon R. Meta-analysis of clinical trials: opportunities and limitations. In: Stangl DK, Berry DA, editors. Meta-Analysis in Medicine and Health Policy. New York: Marcel Dekker, 2000.
- Nissen SE, Wolski K. Effect of rosiglitazone on the risk of myocardial infarction and death from cardiovascular causes. N Engl J Med 2007; 356:2457–2471.
- Turner EH, Matthews AM, Linardatos E, et al. Selective publication of antidepressant trials and its influence on apparent efficacy. N Engl J Med 2008; 358:252–260.
- LeLorier J, Grégoire G, Benhaddad A, Lapierre J, Derderian F. Discrepancies between meta-analyses and subsequent large randomized, controlled trials. N Engl J Med 1997; 337:536–542.
- Steinbrook R. Searching for the right search—reaching the medical literature. N Engl J Med 2006; 354:4–7.
- Dickersin K, Scherer R, Lefebvre C. Systematic reviews: identifying relevant studies for systematic reviews. BMJ 1994; 309:1286–1291.
- De Luca G, Suryapranta H, Stone GW, et al. Coronary stenting versus balloon angioplasty for acute myocardial infarction: a meta-regression analysis of randomized trials. Int J Cardiol 2007; 10.1016/j.ijcard.2007.03.112
- Ng TT, McGory ML, Ko CY, et al. Meta-analysis in surgery. Arch Surg 2006; 141:1125–1130.
- Ray CE, Prochazka A. The need for anticoagulation following inferior vena cava filter placement: systematic review. Cardiovasc Intervent Radiol 2007; 31:316–324.
- Nicolucci A, Grilli R, Alexanian AA, Apolone G, Torri V, Liberati A. Quality evolution and clinical implications of randomized controlled trials on the treatment of lung cancer. A lost opportunity for meta-analysis. JAMA 1989; 262:2101–2107.
- Marsoni S, Torri V, Taiana A. Critical review of the quality and development of randomized clinical trials and their influence on the treatment of advanced epithelial ovarian cancer. Ann Oncol 1990; 1:343–350.
- Moher D, Cook DJ, Eastwood S, Olkin I, Rennie D, Stroup DF. Improving the quality of reports of meta-analyses of randomised controlled trials: the QUOROM statement. Quality of Reporting of Meta-analyses. Lancet 1999; 354:1896–1900.
- Gami AS, Witt BJ, Howard DE, et al. Metabolic syndrome and risk of incident cardiovascular events and death. J Am Coll Cardiol 2007; 49:403–414.
- Terrin N, Schmid CH, Lau J, Olkin I. Adjusting for publication bias in the presence of heterogeneity. Stat Med 2003; 22:2113–2126.
- Dentali F, Doukelis D, Gianni M, et al. Meta-analysis: anticoagulant prophylaxis to prevent symptomatic venous thromboembolism in hospitalized medical patients. Ann Intern Med 2007; 146:278–288.
- Whitehead A. Meta-Analysis of Controlled Clinical Trials. New York: Wiley, 2002.
- Gebski V, Burmeister B, Smithers BM, et al. Survival benefits from neoadjuvant chemoradiotherapy or chemotherapy in oesophageal carcinoma: a meta-analysis. Lancet Oncology 2007; 8:226–234.
- Trivella M, Pezzella F, Pastorino U, et al. Microvessel density as a prognostic factor in non-small-cell lung carcinoma: a meta-analysis of individual patient data. Lancet Oncology 2007; 8:488–499.
- Kunz R, Vist G, Oxman AD. Randomisation to protect against selection bias in healthcare trials (Cochrane Methodology Review). The Cochrane Library, 1, 2003. Oxford: Update Software.
- Gillum LA, Mamidipudi SK, Johnston SC. Ischemic stroke risk with oral contraceptives: a meta-analysis. JAMA 2000; 284:72–78.
- Chan WS, Ray J, Wai EK, et al. Risk of stroke in women exposed to low-dose oral contraceptives. Arch Intern Med 2004; 164:741–747.
- Gillum LA, Johnston SC. Oral contraceptives and stroke risk: the debate continues. Lancet 2004; 3:453–454.
- Bhutta AT, Cleves MA, Casey PH, et al. Cognitive and behavioral outcomes of school–aged children who were born preterm. JAMA 2002; 288:728–737.
- De Luca G, Suryapranta H, Stone GW, et al. Adjunctive mechanical devices to prevent distal embolization in patients undergoing mechanical revascularization for acute myocardial infarction: a meta-analysis of randomized trials. Am Heart J 2007; 153:343–353.
- Wang R, Lagakos SW, Ware JH, et al. Statistics in medicine—reporting of subgroup analyses in clinical trials. N Engl J Med 2007; 357:2189–2194.
- Shuster JJ, Jones LS, Salmon DA. Fixed vs random effects meta-analysis in rare events: the rosiglitazone link with myocardial infarction and cardiac death. Stat Med 2007; 26:4375–4385.
- Bracken MB. Rosiglitazone and cardiovascular risk. N Engl J Med 2007; 357:937–938.
- Sutton AJ, Lambert PC, Hellmich M, et al. Meta-analysis in practice: a critical review of available software. In:Stangl DK, Berry DA, editors. Meta-Analysis in Medicine and Health Policy. New York: Marcel Dekker, 2000.
- Berlin JA, Colditz GA. The role of meta-analysis in the regulatory process for food, drugs, and devices. JAMA 1999; 281:830–834.
- Bailar JC. The promise and problems of meta-analysis. N Engl J Med 1997; 337:559–561.
- Simon R. Meta-analysis of clinical trials: opportunities and limitations. In: Stangl DK, Berry DA, editors. Meta-Analysis in Medicine and Health Policy. New York: Marcel Dekker, 2000.
- Nissen SE, Wolski K. Effect of rosiglitazone on the risk of myocardial infarction and death from cardiovascular causes. N Engl J Med 2007; 356:2457–2471.
- Turner EH, Matthews AM, Linardatos E, et al. Selective publication of antidepressant trials and its influence on apparent efficacy. N Engl J Med 2008; 358:252–260.
- LeLorier J, Grégoire G, Benhaddad A, Lapierre J, Derderian F. Discrepancies between meta-analyses and subsequent large randomized, controlled trials. N Engl J Med 1997; 337:536–542.
- Steinbrook R. Searching for the right search—reaching the medical literature. N Engl J Med 2006; 354:4–7.
- Dickersin K, Scherer R, Lefebvre C. Systematic reviews: identifying relevant studies for systematic reviews. BMJ 1994; 309:1286–1291.
- De Luca G, Suryapranta H, Stone GW, et al. Coronary stenting versus balloon angioplasty for acute myocardial infarction: a meta-regression analysis of randomized trials. Int J Cardiol 2007; 10.1016/j.ijcard.2007.03.112
- Ng TT, McGory ML, Ko CY, et al. Meta-analysis in surgery. Arch Surg 2006; 141:1125–1130.
- Ray CE, Prochazka A. The need for anticoagulation following inferior vena cava filter placement: systematic review. Cardiovasc Intervent Radiol 2007; 31:316–324.
- Nicolucci A, Grilli R, Alexanian AA, Apolone G, Torri V, Liberati A. Quality evolution and clinical implications of randomized controlled trials on the treatment of lung cancer. A lost opportunity for meta-analysis. JAMA 1989; 262:2101–2107.
- Marsoni S, Torri V, Taiana A. Critical review of the quality and development of randomized clinical trials and their influence on the treatment of advanced epithelial ovarian cancer. Ann Oncol 1990; 1:343–350.
- Moher D, Cook DJ, Eastwood S, Olkin I, Rennie D, Stroup DF. Improving the quality of reports of meta-analyses of randomised controlled trials: the QUOROM statement. Quality of Reporting of Meta-analyses. Lancet 1999; 354:1896–1900.
- Gami AS, Witt BJ, Howard DE, et al. Metabolic syndrome and risk of incident cardiovascular events and death. J Am Coll Cardiol 2007; 49:403–414.
- Terrin N, Schmid CH, Lau J, Olkin I. Adjusting for publication bias in the presence of heterogeneity. Stat Med 2003; 22:2113–2126.
- Dentali F, Doukelis D, Gianni M, et al. Meta-analysis: anticoagulant prophylaxis to prevent symptomatic venous thromboembolism in hospitalized medical patients. Ann Intern Med 2007; 146:278–288.
- Whitehead A. Meta-Analysis of Controlled Clinical Trials. New York: Wiley, 2002.
- Gebski V, Burmeister B, Smithers BM, et al. Survival benefits from neoadjuvant chemoradiotherapy or chemotherapy in oesophageal carcinoma: a meta-analysis. Lancet Oncology 2007; 8:226–234.
- Trivella M, Pezzella F, Pastorino U, et al. Microvessel density as a prognostic factor in non-small-cell lung carcinoma: a meta-analysis of individual patient data. Lancet Oncology 2007; 8:488–499.
- Kunz R, Vist G, Oxman AD. Randomisation to protect against selection bias in healthcare trials (Cochrane Methodology Review). The Cochrane Library, 1, 2003. Oxford: Update Software.
- Gillum LA, Mamidipudi SK, Johnston SC. Ischemic stroke risk with oral contraceptives: a meta-analysis. JAMA 2000; 284:72–78.
- Chan WS, Ray J, Wai EK, et al. Risk of stroke in women exposed to low-dose oral contraceptives. Arch Intern Med 2004; 164:741–747.
- Gillum LA, Johnston SC. Oral contraceptives and stroke risk: the debate continues. Lancet 2004; 3:453–454.
- Bhutta AT, Cleves MA, Casey PH, et al. Cognitive and behavioral outcomes of school–aged children who were born preterm. JAMA 2002; 288:728–737.
- De Luca G, Suryapranta H, Stone GW, et al. Adjunctive mechanical devices to prevent distal embolization in patients undergoing mechanical revascularization for acute myocardial infarction: a meta-analysis of randomized trials. Am Heart J 2007; 153:343–353.
- Wang R, Lagakos SW, Ware JH, et al. Statistics in medicine—reporting of subgroup analyses in clinical trials. N Engl J Med 2007; 357:2189–2194.
- Shuster JJ, Jones LS, Salmon DA. Fixed vs random effects meta-analysis in rare events: the rosiglitazone link with myocardial infarction and cardiac death. Stat Med 2007; 26:4375–4385.
- Bracken MB. Rosiglitazone and cardiovascular risk. N Engl J Med 2007; 357:937–938.
- Sutton AJ, Lambert PC, Hellmich M, et al. Meta-analysis in practice: a critical review of available software. In:Stangl DK, Berry DA, editors. Meta-Analysis in Medicine and Health Policy. New York: Marcel Dekker, 2000.
KEY POINTS
- Meta-analysis is an analytical technique designed to summarize the results of multiple studies.
- By combining studies, a meta-analysis increases the sample size and thus the power to study effects of interest.
- There are many caveats in performing a valid meta-analysis, and in some cases a meta-analysis is not appropriate and the results can be misleading.