User login
Methodological Progress Note: Classification and Regression Tree Analysis
Machine-learning is a type of artificial intelligence in which systems automatically learn and improve from experience without being explicitly programmed. Classification and Regression Tree (CART) analysis is a machine-learning algorithm that was developed to visually classify or segment populations into subgroups with similar characteristics and outcomes. CART analysis is a decision tree methodology that was initially developed in the 1960s for use in product marketing.1 Since then, a number of health disciplines have used it to isolate patient subgroups from larger populations to guide clinical decision-making by better identifying those most likely to benefit.2 The clinical utility of CART mirrors how most clinicians think, which is not in terms of coefficients (ie, regression output) but rather in terms of categories or classifications (eg, low vs high risk).
In this issue of the Journal of Hospital Medicine, Young and colleagues use classification trees to predict discharge placement (postacute care facility vs home) based on a patient’s hospital admission characteristics and mobility score. The resulting decision tree indicates that patients with the lowest mobility scores, as well as those 65 years and older, were most likely to be discharged to postacute care facilities.3 In this review, we orient the reader to the basics of CART analysis, discuss important intricacies, and weigh its pros, cons, and application as a statistical tool.
WHAT IS CART ANALYSIS?
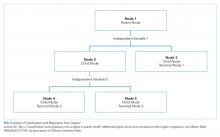
CART is a nonparametric (ie, makes no assumptions about data distribution) statistical tool that identifies subgroups within a population whose members share common characteristics as defined by the independent variables included in the model. CART analysis is unique in that it yields a visual output of the data in the form of a multisegmented structure that resembles the branches of a tree (Figure). CART analysis consists of four basic steps: (1) tree-building (including splitting criteria and estimation of classification error), (2) stopping the tree-building process, (3) tree “pruning,” and (4) tree selection.
In general, CART analysis begins with a single “node” or group, which contains the entire sample population. This is referred to as the “parent node.” The CART procedure simultaneously examines all available independent variables and selects one that results in two groups that are the most distinct with respect to the outcome variable of interest. In Young et al’s example, posthospital discharge placement is the outcome.3 This parent node then branches into two “child nodes” according to the independent variable that was selected. Within each of these “child nodes,” the tree-growing methodology recursively assesses each of the remaining independent variables to determine which will result in the best split according to the chosen splitting criterion.2 Each subsequent “child node” will become a “parent node” to the two groups in which it splits. This process is repeated on the data in each subsequent “child node” and is stopped once a predefined stopping point is reached. Notably, while division into two groups is the most common application of CART modeling, there are models that can split data into more than two child nodes.
Since CART outcomes can be heavily dependent on the data being used (eg, electronic health records or administrative data), it is important to attempt to confirm results in a similar, but different, study cohort. Because obtaining separate data sources with similar cohorts can be difficult, many investigators using CART will utilize a “split sample approach” in which study data are split into separate training and validation sets.4 In the training set, which frequently comprises two-thirds of the available data, the algorithm is tested in exploratory analysis. Once the algorithm is defined and agreed upon, it is retested within a validation set, constructed from the remaining one-third of data. This approach, which Young et al utilize,3 allows for improved confidence and reduced risk of bias in the findings and allows for some degree of external validation. Further, the split sample approach supports more reliable measures of predictive accuracy: in Young et al’s case, the proportion of correctly classified patients discharged to a postacute care facility (sensitivity: 58%, 95% CI 49-68%) and the proportion of correctly classified patients discharged home (specificity: 84%, 95% CI 78-90%). Despite these advantages, the split sample approach is not universally used.
Classification Versus Regression Trees
While commonly grouped together, CARTs can be distinguished from one another based on the dependent, or outcome, variable. Categorical outcome variables require the use of a classification tree, while continuous outcomes utilize regression trees. Of note, the independent, or predictor, variables can be any combination of categorical or continuous variables. However, splitting at each node creates categorical output when using CART algorithms.
Splitting Criteria
The splitting of each node is based on reducing the degree of “impurity” (heterogeneity with respect to the outcome variable) within each node. For example, a node that has no impurity will have a zero error rate labeling its binary outcomes. While CART works well with categorical variables, continuous variables (eg, age) can also be assessed, though only with certain algorithms. Several different splitting criteria exist, each of which attempt to maximize the differences within each child node. While beyond the scope of this review, examples of popular splitting criteria are Gini, entropy, and minimum error.5
Stopping Rules
To manage the size of a tree, CART analysis allows for predefined stopping rules to minimize the extent of growth while also establishing a minimal degree of statistical difference between nodes that is considered meaningful. To accomplish this task, two stopping rules are often used. The first defines the minimum number of observations in child, or “terminal,” nodes. The second defines the maximum number of levels a tree may grow, thus allowing the investigator to decide the total number of predictor variables that can define a terminal node. While several other stopping rules exist, these are the most commonly utilized.
Pruning
To avoid missing important associations due to premature stoppage, investigators may use another mechanism to limit tree growth called “pruning.” For pruning, the first step is to grow a considerably large tree that includes many levels or nodes, possibly to the point where there are just a few observations per terminal node. Then, similar to the residual sum of squares in a regression, the investigator can calculate a misclassification cost (ie, goodness of fit) and select the tree with the smallest cost.2 Of note, stopping rules and pruning can be used simultaneously.
Classification Error
Similar to other forms of statistical inference it remains important to understand the uncertainty within the inference. In regression modeling, for example, classification errors can be calculated using standard errors of the parameter estimates. In CART analysis, because random samples from a population may produce different trees, measures of variability can be more complicated. One strategy is to generate a tree from a test sample and then use the remaining data to calculate a measure of the misclassification cost (a measure of how much additional accuracy a split must add to the entire tree to warrant the additional complexity). Alternatively, a “k-fold cross-validation” can be performed in which the data is broken down into k subsets from which a tree is created using all data except for one of the subsets. The computed tree is then applied to the remaining subset to determine a misclassification cost. These classification costs are important as they also impact the stopping and pruning processes. Ultimately, a final tree, which best limits classification errors, is selected.
WHEN WOULD YOU USE CART ANALYSIS?
This method can be useful in multiple settings in which an investigator wants to characterize a subpopulation from a larger cohort. Adaptation of this could include, but is not limited to, risk stratification,6 diagnostics,7 and patient identification for medical interventions.8 Moreover, CART analysis has the added benefit of creating visually interpretable predictive models that can be utilized for front-line clinical decision making.9,10
STRENGTHS OF CART ANALYSIS
CART analysis has been shown to have several advantages over other commonly used modeling methods. First, it is a nonparametric model that can handle highly skewed data and does not require that the predictor, or predictors, takes on a predetermined form (allowing them to be constructed from the data). This is helpful as many clinical variables can have wide degrees of variance.
Unlike other modeling techniques, CART can identify higher-order interactions between multiple variables, meaning it can handle interactions that occur whenever one variable affects the nature of an interaction between two other variables. Further, CART can handle multiple correlated independent variables, something logistic regression models classically cannot do.
From a clinical standpoint, the “logic” of the visual-based CART output can be easier to interpret than the probabilistic output (eg, odds ratio) associated with logistic regression modeling, making it more practical, applicable, and easier for clinicians to adopt.10,12 Finally, CART software is easy to use for those who do not have strong statistical backgrounds, and it is less resource intensive than other statistical methods.2
LIMITATIONS OF CART ANALYSIS
Despite these features, CART does have several disadvantages. First, due to the ease with which CART analysis can be performed, “data dredging” can be a significant concern. Its ideal use is with a priori consideration of independent variables.2 Second, while CART is most beneficial in describing links and cutoffs between variables, it may not be useful for hypothesis testing.2 Third, large data sets are needed to perform CART, especially if the investigator is using the split sample approach mentioned above.11 Finally, while CART is the most utilized decision tree methodology, several other types of decision tree methods exist: C4.5, CRUISE, Quick, Unbiased, Efficient Statistical Trees, Chi-square-Automatic-Interaction-Detection, and others. Many of these allow for splitting into more than two groups and have other features that may be more advantageous to one’s analysis.13
WHY DID THE AUTHORS USE CART?
Decision trees offer simple, interpretable results of multiple factors that can be easily applied to clinical scenarios. In this case, the authors specifically used classification tree analysis to take advantage of CART’s machine-learning ability to consider higher-order interactions to build their model—as they lacked a priori evidence to help guide them in traditional (ie, logistic regression) model construction. Furthermore, CART analysis created an output that logically and visually illustrates which combination of characteristics is most associated with discharge placement and can potentially be utilized to help facilitate discharge planning in future hospitalized patients. To sum up, this machine-learning methodology allowed the investigators to determine which variables taken together were the most suitable in predicting their outcome of interest and present these findings in a manner that busy clinicians can interpret and apply.
1. Magee JF. Decision Trees for Decision Making. Harvard Business Review. 1964. https://hbr.org/1964/07/decision-trees-for-decision-making. Accessed August 26, 2019.
2. Lemon SC, Roy J, Clark MA, Friedmann PD, Rakowski W. Classification and regression tree analysis in public health: methodological review and comparison with logistic regression. Ann Behav Med. 2003;26(3):172-181. https://doi.org/10.1207/S15324796ABM2603_02
3. Young D, Colantuoni E, Seltzer D, et al. Prediction of disposition within 48-hours of hospital admission using patient mobility scores. J Hosp Med. 2020;15(9):540-543. https://doi.org/10.12788/jhm.3332
4. Rajkomar A, Dean J, Kohane I. Machine learning in medicine. N Engl J Med. 2019;380(14):1347-1358. https://doi.org/10.1056/NEJMra1814259
5. Zhang H, Singer B. Recursive Partitioning in the Health Sciences. New York: Springer-Verlag; 1999. https://www.springer.com/gp/book/9781475730272. Accessed August 24, 2019.
6. Fonarow GC, Adams KF, Abraham WT, Yancy CW, Boscardin WJ, for the ADHERE Scientific Advisory Committee SG. Risk stratification for in-hospital mortality in acutely decompensated heart failure: classification and regression tree analysis. JAMA. 2005;293(5):572-580. https://doi.org/10.1001/jama.293.5.572
7. Hess KR, Abbruzzese MC, Lenzi R, Raber MN, Abbruzzese JL. Classification and regression tree analysis of 1000 consecutive patients with unknown primary carcinoma. Clin Cancer Res. 1999;5(11):3403-3410.
8. Garzotto M, Beer TM, Hudson RG, et al. Improved detection of prostate cancer using classification and regression tree analysis. J Clin Oncol. 2005;23(19):4322-4329. https://doi.org/10.1200/JCO.2005.11.136
9. Hong W, Dong L, Huang Q, Wu W, Wu J, Wang Y. Prediction of severe acute pancreatitis using classification and regression tree analysis. Dig Dis Sci. 2011;56(12):3664-3671. https://doi.org/10.1007/s10620-011-1849-x
10. Lewis RJ. An Introduction to Classification and Regression Tree (CART) Analysis. Proceedings of Annual Meeting of the Society for Academic Emergency Medicine, San Francisco, CA, USA, May 22-25, 2000; pp. 1–14.
11. Perlich C, Provost F, Simonoff JS. Tree induction vs logistic regression: a learning-curve analysis. J Mach Learn Res. 2003;4(Jun):211-255. https://doi.org/10.1162/153244304322972694
12. Woolever D. The art and science of clinical decision making. Fam Pract Manag. 2008;15(5):31-36.
13. Loh WY. Classification and regression trees. Wires Data Min Know Disc. 2011;1(1):14-23. https://doi.org/10.1002/widm.8
Machine-learning is a type of artificial intelligence in which systems automatically learn and improve from experience without being explicitly programmed. Classification and Regression Tree (CART) analysis is a machine-learning algorithm that was developed to visually classify or segment populations into subgroups with similar characteristics and outcomes. CART analysis is a decision tree methodology that was initially developed in the 1960s for use in product marketing.1 Since then, a number of health disciplines have used it to isolate patient subgroups from larger populations to guide clinical decision-making by better identifying those most likely to benefit.2 The clinical utility of CART mirrors how most clinicians think, which is not in terms of coefficients (ie, regression output) but rather in terms of categories or classifications (eg, low vs high risk).
In this issue of the Journal of Hospital Medicine, Young and colleagues use classification trees to predict discharge placement (postacute care facility vs home) based on a patient’s hospital admission characteristics and mobility score. The resulting decision tree indicates that patients with the lowest mobility scores, as well as those 65 years and older, were most likely to be discharged to postacute care facilities.3 In this review, we orient the reader to the basics of CART analysis, discuss important intricacies, and weigh its pros, cons, and application as a statistical tool.
WHAT IS CART ANALYSIS?
CART is a nonparametric (ie, makes no assumptions about data distribution) statistical tool that identifies subgroups within a population whose members share common characteristics as defined by the independent variables included in the model. CART analysis is unique in that it yields a visual output of the data in the form of a multisegmented structure that resembles the branches of a tree (Figure). CART analysis consists of four basic steps: (1) tree-building (including splitting criteria and estimation of classification error), (2) stopping the tree-building process, (3) tree “pruning,” and (4) tree selection.
In general, CART analysis begins with a single “node” or group, which contains the entire sample population. This is referred to as the “parent node.” The CART procedure simultaneously examines all available independent variables and selects one that results in two groups that are the most distinct with respect to the outcome variable of interest. In Young et al’s example, posthospital discharge placement is the outcome.3 This parent node then branches into two “child nodes” according to the independent variable that was selected. Within each of these “child nodes,” the tree-growing methodology recursively assesses each of the remaining independent variables to determine which will result in the best split according to the chosen splitting criterion.2 Each subsequent “child node” will become a “parent node” to the two groups in which it splits. This process is repeated on the data in each subsequent “child node” and is stopped once a predefined stopping point is reached. Notably, while division into two groups is the most common application of CART modeling, there are models that can split data into more than two child nodes.
Since CART outcomes can be heavily dependent on the data being used (eg, electronic health records or administrative data), it is important to attempt to confirm results in a similar, but different, study cohort. Because obtaining separate data sources with similar cohorts can be difficult, many investigators using CART will utilize a “split sample approach” in which study data are split into separate training and validation sets.4 In the training set, which frequently comprises two-thirds of the available data, the algorithm is tested in exploratory analysis. Once the algorithm is defined and agreed upon, it is retested within a validation set, constructed from the remaining one-third of data. This approach, which Young et al utilize,3 allows for improved confidence and reduced risk of bias in the findings and allows for some degree of external validation. Further, the split sample approach supports more reliable measures of predictive accuracy: in Young et al’s case, the proportion of correctly classified patients discharged to a postacute care facility (sensitivity: 58%, 95% CI 49-68%) and the proportion of correctly classified patients discharged home (specificity: 84%, 95% CI 78-90%). Despite these advantages, the split sample approach is not universally used.
Classification Versus Regression Trees
While commonly grouped together, CARTs can be distinguished from one another based on the dependent, or outcome, variable. Categorical outcome variables require the use of a classification tree, while continuous outcomes utilize regression trees. Of note, the independent, or predictor, variables can be any combination of categorical or continuous variables. However, splitting at each node creates categorical output when using CART algorithms.
Splitting Criteria
The splitting of each node is based on reducing the degree of “impurity” (heterogeneity with respect to the outcome variable) within each node. For example, a node that has no impurity will have a zero error rate labeling its binary outcomes. While CART works well with categorical variables, continuous variables (eg, age) can also be assessed, though only with certain algorithms. Several different splitting criteria exist, each of which attempt to maximize the differences within each child node. While beyond the scope of this review, examples of popular splitting criteria are Gini, entropy, and minimum error.5
Stopping Rules
To manage the size of a tree, CART analysis allows for predefined stopping rules to minimize the extent of growth while also establishing a minimal degree of statistical difference between nodes that is considered meaningful. To accomplish this task, two stopping rules are often used. The first defines the minimum number of observations in child, or “terminal,” nodes. The second defines the maximum number of levels a tree may grow, thus allowing the investigator to decide the total number of predictor variables that can define a terminal node. While several other stopping rules exist, these are the most commonly utilized.
Pruning
To avoid missing important associations due to premature stoppage, investigators may use another mechanism to limit tree growth called “pruning.” For pruning, the first step is to grow a considerably large tree that includes many levels or nodes, possibly to the point where there are just a few observations per terminal node. Then, similar to the residual sum of squares in a regression, the investigator can calculate a misclassification cost (ie, goodness of fit) and select the tree with the smallest cost.2 Of note, stopping rules and pruning can be used simultaneously.
Classification Error
Similar to other forms of statistical inference it remains important to understand the uncertainty within the inference. In regression modeling, for example, classification errors can be calculated using standard errors of the parameter estimates. In CART analysis, because random samples from a population may produce different trees, measures of variability can be more complicated. One strategy is to generate a tree from a test sample and then use the remaining data to calculate a measure of the misclassification cost (a measure of how much additional accuracy a split must add to the entire tree to warrant the additional complexity). Alternatively, a “k-fold cross-validation” can be performed in which the data is broken down into k subsets from which a tree is created using all data except for one of the subsets. The computed tree is then applied to the remaining subset to determine a misclassification cost. These classification costs are important as they also impact the stopping and pruning processes. Ultimately, a final tree, which best limits classification errors, is selected.
WHEN WOULD YOU USE CART ANALYSIS?
This method can be useful in multiple settings in which an investigator wants to characterize a subpopulation from a larger cohort. Adaptation of this could include, but is not limited to, risk stratification,6 diagnostics,7 and patient identification for medical interventions.8 Moreover, CART analysis has the added benefit of creating visually interpretable predictive models that can be utilized for front-line clinical decision making.9,10
STRENGTHS OF CART ANALYSIS
CART analysis has been shown to have several advantages over other commonly used modeling methods. First, it is a nonparametric model that can handle highly skewed data and does not require that the predictor, or predictors, takes on a predetermined form (allowing them to be constructed from the data). This is helpful as many clinical variables can have wide degrees of variance.
Unlike other modeling techniques, CART can identify higher-order interactions between multiple variables, meaning it can handle interactions that occur whenever one variable affects the nature of an interaction between two other variables. Further, CART can handle multiple correlated independent variables, something logistic regression models classically cannot do.
From a clinical standpoint, the “logic” of the visual-based CART output can be easier to interpret than the probabilistic output (eg, odds ratio) associated with logistic regression modeling, making it more practical, applicable, and easier for clinicians to adopt.10,12 Finally, CART software is easy to use for those who do not have strong statistical backgrounds, and it is less resource intensive than other statistical methods.2
LIMITATIONS OF CART ANALYSIS
Despite these features, CART does have several disadvantages. First, due to the ease with which CART analysis can be performed, “data dredging” can be a significant concern. Its ideal use is with a priori consideration of independent variables.2 Second, while CART is most beneficial in describing links and cutoffs between variables, it may not be useful for hypothesis testing.2 Third, large data sets are needed to perform CART, especially if the investigator is using the split sample approach mentioned above.11 Finally, while CART is the most utilized decision tree methodology, several other types of decision tree methods exist: C4.5, CRUISE, Quick, Unbiased, Efficient Statistical Trees, Chi-square-Automatic-Interaction-Detection, and others. Many of these allow for splitting into more than two groups and have other features that may be more advantageous to one’s analysis.13
WHY DID THE AUTHORS USE CART?
Decision trees offer simple, interpretable results of multiple factors that can be easily applied to clinical scenarios. In this case, the authors specifically used classification tree analysis to take advantage of CART’s machine-learning ability to consider higher-order interactions to build their model—as they lacked a priori evidence to help guide them in traditional (ie, logistic regression) model construction. Furthermore, CART analysis created an output that logically and visually illustrates which combination of characteristics is most associated with discharge placement and can potentially be utilized to help facilitate discharge planning in future hospitalized patients. To sum up, this machine-learning methodology allowed the investigators to determine which variables taken together were the most suitable in predicting their outcome of interest and present these findings in a manner that busy clinicians can interpret and apply.
Machine-learning is a type of artificial intelligence in which systems automatically learn and improve from experience without being explicitly programmed. Classification and Regression Tree (CART) analysis is a machine-learning algorithm that was developed to visually classify or segment populations into subgroups with similar characteristics and outcomes. CART analysis is a decision tree methodology that was initially developed in the 1960s for use in product marketing.1 Since then, a number of health disciplines have used it to isolate patient subgroups from larger populations to guide clinical decision-making by better identifying those most likely to benefit.2 The clinical utility of CART mirrors how most clinicians think, which is not in terms of coefficients (ie, regression output) but rather in terms of categories or classifications (eg, low vs high risk).
In this issue of the Journal of Hospital Medicine, Young and colleagues use classification trees to predict discharge placement (postacute care facility vs home) based on a patient’s hospital admission characteristics and mobility score. The resulting decision tree indicates that patients with the lowest mobility scores, as well as those 65 years and older, were most likely to be discharged to postacute care facilities.3 In this review, we orient the reader to the basics of CART analysis, discuss important intricacies, and weigh its pros, cons, and application as a statistical tool.
WHAT IS CART ANALYSIS?
CART is a nonparametric (ie, makes no assumptions about data distribution) statistical tool that identifies subgroups within a population whose members share common characteristics as defined by the independent variables included in the model. CART analysis is unique in that it yields a visual output of the data in the form of a multisegmented structure that resembles the branches of a tree (Figure). CART analysis consists of four basic steps: (1) tree-building (including splitting criteria and estimation of classification error), (2) stopping the tree-building process, (3) tree “pruning,” and (4) tree selection.
In general, CART analysis begins with a single “node” or group, which contains the entire sample population. This is referred to as the “parent node.” The CART procedure simultaneously examines all available independent variables and selects one that results in two groups that are the most distinct with respect to the outcome variable of interest. In Young et al’s example, posthospital discharge placement is the outcome.3 This parent node then branches into two “child nodes” according to the independent variable that was selected. Within each of these “child nodes,” the tree-growing methodology recursively assesses each of the remaining independent variables to determine which will result in the best split according to the chosen splitting criterion.2 Each subsequent “child node” will become a “parent node” to the two groups in which it splits. This process is repeated on the data in each subsequent “child node” and is stopped once a predefined stopping point is reached. Notably, while division into two groups is the most common application of CART modeling, there are models that can split data into more than two child nodes.
Since CART outcomes can be heavily dependent on the data being used (eg, electronic health records or administrative data), it is important to attempt to confirm results in a similar, but different, study cohort. Because obtaining separate data sources with similar cohorts can be difficult, many investigators using CART will utilize a “split sample approach” in which study data are split into separate training and validation sets.4 In the training set, which frequently comprises two-thirds of the available data, the algorithm is tested in exploratory analysis. Once the algorithm is defined and agreed upon, it is retested within a validation set, constructed from the remaining one-third of data. This approach, which Young et al utilize,3 allows for improved confidence and reduced risk of bias in the findings and allows for some degree of external validation. Further, the split sample approach supports more reliable measures of predictive accuracy: in Young et al’s case, the proportion of correctly classified patients discharged to a postacute care facility (sensitivity: 58%, 95% CI 49-68%) and the proportion of correctly classified patients discharged home (specificity: 84%, 95% CI 78-90%). Despite these advantages, the split sample approach is not universally used.
Classification Versus Regression Trees
While commonly grouped together, CARTs can be distinguished from one another based on the dependent, or outcome, variable. Categorical outcome variables require the use of a classification tree, while continuous outcomes utilize regression trees. Of note, the independent, or predictor, variables can be any combination of categorical or continuous variables. However, splitting at each node creates categorical output when using CART algorithms.
Splitting Criteria
The splitting of each node is based on reducing the degree of “impurity” (heterogeneity with respect to the outcome variable) within each node. For example, a node that has no impurity will have a zero error rate labeling its binary outcomes. While CART works well with categorical variables, continuous variables (eg, age) can also be assessed, though only with certain algorithms. Several different splitting criteria exist, each of which attempt to maximize the differences within each child node. While beyond the scope of this review, examples of popular splitting criteria are Gini, entropy, and minimum error.5
Stopping Rules
To manage the size of a tree, CART analysis allows for predefined stopping rules to minimize the extent of growth while also establishing a minimal degree of statistical difference between nodes that is considered meaningful. To accomplish this task, two stopping rules are often used. The first defines the minimum number of observations in child, or “terminal,” nodes. The second defines the maximum number of levels a tree may grow, thus allowing the investigator to decide the total number of predictor variables that can define a terminal node. While several other stopping rules exist, these are the most commonly utilized.
Pruning
To avoid missing important associations due to premature stoppage, investigators may use another mechanism to limit tree growth called “pruning.” For pruning, the first step is to grow a considerably large tree that includes many levels or nodes, possibly to the point where there are just a few observations per terminal node. Then, similar to the residual sum of squares in a regression, the investigator can calculate a misclassification cost (ie, goodness of fit) and select the tree with the smallest cost.2 Of note, stopping rules and pruning can be used simultaneously.
Classification Error
Similar to other forms of statistical inference it remains important to understand the uncertainty within the inference. In regression modeling, for example, classification errors can be calculated using standard errors of the parameter estimates. In CART analysis, because random samples from a population may produce different trees, measures of variability can be more complicated. One strategy is to generate a tree from a test sample and then use the remaining data to calculate a measure of the misclassification cost (a measure of how much additional accuracy a split must add to the entire tree to warrant the additional complexity). Alternatively, a “k-fold cross-validation” can be performed in which the data is broken down into k subsets from which a tree is created using all data except for one of the subsets. The computed tree is then applied to the remaining subset to determine a misclassification cost. These classification costs are important as they also impact the stopping and pruning processes. Ultimately, a final tree, which best limits classification errors, is selected.
WHEN WOULD YOU USE CART ANALYSIS?
This method can be useful in multiple settings in which an investigator wants to characterize a subpopulation from a larger cohort. Adaptation of this could include, but is not limited to, risk stratification,6 diagnostics,7 and patient identification for medical interventions.8 Moreover, CART analysis has the added benefit of creating visually interpretable predictive models that can be utilized for front-line clinical decision making.9,10
STRENGTHS OF CART ANALYSIS
CART analysis has been shown to have several advantages over other commonly used modeling methods. First, it is a nonparametric model that can handle highly skewed data and does not require that the predictor, or predictors, takes on a predetermined form (allowing them to be constructed from the data). This is helpful as many clinical variables can have wide degrees of variance.
Unlike other modeling techniques, CART can identify higher-order interactions between multiple variables, meaning it can handle interactions that occur whenever one variable affects the nature of an interaction between two other variables. Further, CART can handle multiple correlated independent variables, something logistic regression models classically cannot do.
From a clinical standpoint, the “logic” of the visual-based CART output can be easier to interpret than the probabilistic output (eg, odds ratio) associated with logistic regression modeling, making it more practical, applicable, and easier for clinicians to adopt.10,12 Finally, CART software is easy to use for those who do not have strong statistical backgrounds, and it is less resource intensive than other statistical methods.2
LIMITATIONS OF CART ANALYSIS
Despite these features, CART does have several disadvantages. First, due to the ease with which CART analysis can be performed, “data dredging” can be a significant concern. Its ideal use is with a priori consideration of independent variables.2 Second, while CART is most beneficial in describing links and cutoffs between variables, it may not be useful for hypothesis testing.2 Third, large data sets are needed to perform CART, especially if the investigator is using the split sample approach mentioned above.11 Finally, while CART is the most utilized decision tree methodology, several other types of decision tree methods exist: C4.5, CRUISE, Quick, Unbiased, Efficient Statistical Trees, Chi-square-Automatic-Interaction-Detection, and others. Many of these allow for splitting into more than two groups and have other features that may be more advantageous to one’s analysis.13
WHY DID THE AUTHORS USE CART?
Decision trees offer simple, interpretable results of multiple factors that can be easily applied to clinical scenarios. In this case, the authors specifically used classification tree analysis to take advantage of CART’s machine-learning ability to consider higher-order interactions to build their model—as they lacked a priori evidence to help guide them in traditional (ie, logistic regression) model construction. Furthermore, CART analysis created an output that logically and visually illustrates which combination of characteristics is most associated with discharge placement and can potentially be utilized to help facilitate discharge planning in future hospitalized patients. To sum up, this machine-learning methodology allowed the investigators to determine which variables taken together were the most suitable in predicting their outcome of interest and present these findings in a manner that busy clinicians can interpret and apply.
1. Magee JF. Decision Trees for Decision Making. Harvard Business Review. 1964. https://hbr.org/1964/07/decision-trees-for-decision-making. Accessed August 26, 2019.
2. Lemon SC, Roy J, Clark MA, Friedmann PD, Rakowski W. Classification and regression tree analysis in public health: methodological review and comparison with logistic regression. Ann Behav Med. 2003;26(3):172-181. https://doi.org/10.1207/S15324796ABM2603_02
3. Young D, Colantuoni E, Seltzer D, et al. Prediction of disposition within 48-hours of hospital admission using patient mobility scores. J Hosp Med. 2020;15(9):540-543. https://doi.org/10.12788/jhm.3332
4. Rajkomar A, Dean J, Kohane I. Machine learning in medicine. N Engl J Med. 2019;380(14):1347-1358. https://doi.org/10.1056/NEJMra1814259
5. Zhang H, Singer B. Recursive Partitioning in the Health Sciences. New York: Springer-Verlag; 1999. https://www.springer.com/gp/book/9781475730272. Accessed August 24, 2019.
6. Fonarow GC, Adams KF, Abraham WT, Yancy CW, Boscardin WJ, for the ADHERE Scientific Advisory Committee SG. Risk stratification for in-hospital mortality in acutely decompensated heart failure: classification and regression tree analysis. JAMA. 2005;293(5):572-580. https://doi.org/10.1001/jama.293.5.572
7. Hess KR, Abbruzzese MC, Lenzi R, Raber MN, Abbruzzese JL. Classification and regression tree analysis of 1000 consecutive patients with unknown primary carcinoma. Clin Cancer Res. 1999;5(11):3403-3410.
8. Garzotto M, Beer TM, Hudson RG, et al. Improved detection of prostate cancer using classification and regression tree analysis. J Clin Oncol. 2005;23(19):4322-4329. https://doi.org/10.1200/JCO.2005.11.136
9. Hong W, Dong L, Huang Q, Wu W, Wu J, Wang Y. Prediction of severe acute pancreatitis using classification and regression tree analysis. Dig Dis Sci. 2011;56(12):3664-3671. https://doi.org/10.1007/s10620-011-1849-x
10. Lewis RJ. An Introduction to Classification and Regression Tree (CART) Analysis. Proceedings of Annual Meeting of the Society for Academic Emergency Medicine, San Francisco, CA, USA, May 22-25, 2000; pp. 1–14.
11. Perlich C, Provost F, Simonoff JS. Tree induction vs logistic regression: a learning-curve analysis. J Mach Learn Res. 2003;4(Jun):211-255. https://doi.org/10.1162/153244304322972694
12. Woolever D. The art and science of clinical decision making. Fam Pract Manag. 2008;15(5):31-36.
13. Loh WY. Classification and regression trees. Wires Data Min Know Disc. 2011;1(1):14-23. https://doi.org/10.1002/widm.8
1. Magee JF. Decision Trees for Decision Making. Harvard Business Review. 1964. https://hbr.org/1964/07/decision-trees-for-decision-making. Accessed August 26, 2019.
2. Lemon SC, Roy J, Clark MA, Friedmann PD, Rakowski W. Classification and regression tree analysis in public health: methodological review and comparison with logistic regression. Ann Behav Med. 2003;26(3):172-181. https://doi.org/10.1207/S15324796ABM2603_02
3. Young D, Colantuoni E, Seltzer D, et al. Prediction of disposition within 48-hours of hospital admission using patient mobility scores. J Hosp Med. 2020;15(9):540-543. https://doi.org/10.12788/jhm.3332
4. Rajkomar A, Dean J, Kohane I. Machine learning in medicine. N Engl J Med. 2019;380(14):1347-1358. https://doi.org/10.1056/NEJMra1814259
5. Zhang H, Singer B. Recursive Partitioning in the Health Sciences. New York: Springer-Verlag; 1999. https://www.springer.com/gp/book/9781475730272. Accessed August 24, 2019.
6. Fonarow GC, Adams KF, Abraham WT, Yancy CW, Boscardin WJ, for the ADHERE Scientific Advisory Committee SG. Risk stratification for in-hospital mortality in acutely decompensated heart failure: classification and regression tree analysis. JAMA. 2005;293(5):572-580. https://doi.org/10.1001/jama.293.5.572
7. Hess KR, Abbruzzese MC, Lenzi R, Raber MN, Abbruzzese JL. Classification and regression tree analysis of 1000 consecutive patients with unknown primary carcinoma. Clin Cancer Res. 1999;5(11):3403-3410.
8. Garzotto M, Beer TM, Hudson RG, et al. Improved detection of prostate cancer using classification and regression tree analysis. J Clin Oncol. 2005;23(19):4322-4329. https://doi.org/10.1200/JCO.2005.11.136
9. Hong W, Dong L, Huang Q, Wu W, Wu J, Wang Y. Prediction of severe acute pancreatitis using classification and regression tree analysis. Dig Dis Sci. 2011;56(12):3664-3671. https://doi.org/10.1007/s10620-011-1849-x
10. Lewis RJ. An Introduction to Classification and Regression Tree (CART) Analysis. Proceedings of Annual Meeting of the Society for Academic Emergency Medicine, San Francisco, CA, USA, May 22-25, 2000; pp. 1–14.
11. Perlich C, Provost F, Simonoff JS. Tree induction vs logistic regression: a learning-curve analysis. J Mach Learn Res. 2003;4(Jun):211-255. https://doi.org/10.1162/153244304322972694
12. Woolever D. The art and science of clinical decision making. Fam Pract Manag. 2008;15(5):31-36.
13. Loh WY. Classification and regression trees. Wires Data Min Know Disc. 2011;1(1):14-23. https://doi.org/10.1002/widm.8
© 2020 Society of Hospital Medicine