User login
The TEND (Tomorrow’s Expected Number of Discharges) Model Accurately Predicted the Number of Patients Who Were Discharged from the Hospital the Next Day
Hospitals typically allocate beds based on historical patient volumes. If funding decreases, hospitals will usually try to maximize resource utilization by allocating beds to attain occupancies close to 100% for significant periods of time. This will invariably cause days in which hospital occupancy exceeds capacity, at which time critical entry points (such as the emergency department and operating room) will become blocked. This creates significant concerns over the patient quality of care.
Hospital administrators have very few options when hospital occupancy exceeds 100%. They could postpone admissions for “planned” cases, bring in additional staff to increase capacity, or instigate additional methods to increase hospital discharges such as expanding care resources in the community. All options are costly, bothersome, or cannot be actioned immediately. The need for these options could be minimized by enabling hospital administrators to make more informed decisions regarding hospital bed management by knowing the likely number of discharges in the next 24 hours.
Predicting the number of people who will be discharged in the next day can be approached in several ways. One approach would be to calculate each patient’s expected length of stay and then use the variation around that estimate to calculate each day’s discharge probability. Several studies have attempted to model hospital length of stay using a broad assortment of methodologies, but a mechanism to accurately predict this outcome has been elusive1,2 (with Verburg et al.3 concluding in their study’s abstract that “…it is difficult to predict length of stay…”). A second approach would be to use survival analysis methods to generate each patient’s hazard of discharge over time, which could be directly converted to an expected daily risk of discharge. However, this approach is complicated by the concurrent need to include time-dependent covariates and consider the competing risk of death in hospital, which can complicate survival modeling.4,5 A third approach would be the implementation of a longitudinal analysis using marginal models to predict the daily probability of discharge,6 but this method quickly overwhelms computer resources when large datasets are present.
In this study, we decided to use nonparametric models to predict the daily number of hospital discharges. We first identified patient groups with distinct discharge patterns. We then calculated the conditional daily discharge probability of patients in each of these groups. Finally, these conditional daily discharge probabilities were then summed for each hospital day to generate the expected number of discharges in the next 24 hours. This paper details the methods we used to create our model and the accuracy of its predictions.
METHODS
Study Setting and Databases Used for Analysis
The study took place at The Ottawa Hospital, a 1000-bed teaching hospital with 3 campuses that is the primary referral center in our region. The study was approved by our local research ethics board.
The Patient Registry Database records the date and time of admission for each patient (defined as the moment that a patient’s admission request is registered in the patient registration) and discharge (defined as the time when the patient’s discharge from hospital was entered into the patient registration) for hospital encounters. Emergency department encounters were also identified in the Patient Registry Database along with admission service, patient age and sex, and patient location throughout the admission. The Laboratory Database records all laboratory studies and results on all patients at the hospital.
Study Cohort
We used the Patient Registry Database to identify all people aged 1 year or more who were admitted to the hospital between January 1, 2013, and December 31, 2015. This time frame was selected to (i) ensure that data were complete; and (ii) complete calendar years of data were available for both derivation (patient-days in 2013-2014) and validation (2015) cohorts. Patients who were observed in the emergency room without admission to hospital were not included.
Study Outcome
The study outcome was the number of patients discharged from the hospital each day. For the analysis, the reference point for each day was 1 second past midnight; therefore, values for time-dependent covariates up to and including midnight were used to predict the number of discharges in the next 24 hours.
Study Covariates
Baseline (ie, time-independent) covariates included patient age and sex, admission service, hospital campus, whether or not the patient was admitted from the emergency department (all determined from the Patient Registry Database), and the Laboratory-based Acute Physiological Score (LAPS). The latter, which was calculated with the Laboratory Database using results for 14 tests (arterial pH, PaCO2, PaO2, anion gap, hematocrit, total white blood cell count, serum albumin, total bilirubin, creatinine, urea nitrogen, glucose, sodium, bicarbonate, and troponin I) measured in the 24-hour time frame preceding hospitalization, was derived by Escobar and colleagues7 to measure severity of illness and was subsequently validated in our hospital.8 The independent association of each laboratory perturbation with risk of death in hospital is reflected by the number of points assigned to each lab value with the total LAPS being the sum of these values. Time-dependent covariates included weekday in hospital and whether or not patients were in the intensive care unit.
Analysis
We used 3 stages to create a model to predict the daily expected number of discharges: we identified discharge risk strata containing patients having similar discharge patterns using data from patients in the derivation cohort (first stage); then, we generated the preliminary probability of discharge by determining the daily discharge probability in each discharge risk strata (second stage); finally, we modified the probability from the second stage based on the weekday and admission service and summed these probabilities to create the expected number of discharges on a particular date (third stage).
The first stage identified discharge risk strata based on the covariates listed above. This was determined by using a survival tree approach9 with proportional hazard regression models to generate the “splits.” These models were offered all covariates listed in the Study Covariates section. Admission service was clustered within 4 departments (obstetrics/gynecology, psychiatry, surgery, and medicine) and day of week was “binarized” into weekday/weekend-holiday (because the use of categorical variables with large numbers of groups can “stunt” regression trees due to small numbers of patients—and, therefore, statistical power—in each subgroup). The proportional hazards model identified the covariate having the strongest association with time to discharge (based on the Wald X2 value divided by the degrees of freedom). This variable was then used to split the cohort into subgroups (with continuous covariates being categorized into quartiles). The proportional hazards model was then repeated in each subgroup (with the previous splitting variable[s] excluded from the model). This process continued until no variable was associated with time to discharge with a P value less than .0001. This survival-tree was then used to cluster all patients into distinct discharge risk strata.
In the second stage, we generated the preliminary probability of discharge for a specific date. This was calculated by assigning all patients in hospital to their discharge risk strata (Appendix). We then measured the probability of discharge on each hospitalization day in all discharge risk strata using data from the previous 180 days (we only used the prior 180 days of data to account for temporal changes in hospital discharge patterns). For example, consider a 75-year-old patient on her third hospital day under obstetrics/gynecology on December 19, 2015 (a Saturday). This patient would be assigned to risk stratum #133 (Appendix A). We then measured the probability of discharge of all patients in this discharge risk stratum hospitalized in the previous 6 months (ie, between June 22, 2015, and December 18, 2015) on each hospital day. For risk stratum #133, the probability of discharge on hospital day 3 was 0.1111; therefore, our sample patient’s preliminary expected discharge probability was 0.1111.
To attain stable daily discharge probability estimates, a minimum of 50 patients per discharge risk stratum-hospitalization day combination was required. If there were less than 50 patients for a particular hospitalization day in a particular discharge risk stratum, we grouped hospitalization days in that risk stratum together until the minimum of 50 patients was collected.
The third (and final) stage accounted for the lack of granularity when we created the discharge risk strata in the first stage. As we mentioned above, admission service was clustered into 4 departments and the day of week was clustered into weekend/weekday. However, important variations in discharge probabilities could still exist within departments and between particular days of the week.10 Therefore, we created a correction factor to adjust the preliminary expected number of discharges based on the admission division and day of week. This correction factor used data from the 180 days prior to the analysis date within which the expected daily number of discharges was calculated (using the methods above). The correction factor was the relative difference between the observed and expected number of discharges within each division-day of week grouping.
For example, to calculate the correction factor for our sample patient presented above (75-year-old patient on hospital day 3 under gynecology on Saturday, December 19, 2015), we measured the observed number of discharges from gynecology on Saturdays between June 22, 2015, and December 18, 2015, (n = 206) and the expected number of discharges (n = 195.255) resulting in a correction factor of (observed-expected)/expected = (195.255-206)/195.206 = 0.05503. Therefore, the final expected discharge probability for our sample patient was 0.1111+0.1111*0.05503=0.1172. The expected number of discharges on a particular date was the preliminary expected number of discharges on that date (generated in the second stage) multiplied by the correction factor for the corresponding division-day or week group.
RESULTS
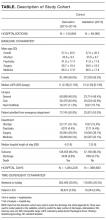
There were 192,859 admissions involving patients more than 1 year of age that spent at least part of their hospitalization between January 1, 2013, and December 31, 2015 (Table). Patients were middle-aged and slightly female predominant, with about half being admitted from the emergency department. Approximately 80% of admissions were to surgical or medical services. More than 95% of admissions ended with a discharge from the hospital with the remainder ending in a death. Almost 30% of hospitalization days occurred on weekends or holidays. Hospitalizations in the derivation (2013-2014) and validation (2015) group were essentially the same, except there was a slight drop in hospital length of stay (from a median of 4 days to 3 days) between the 2 periods.
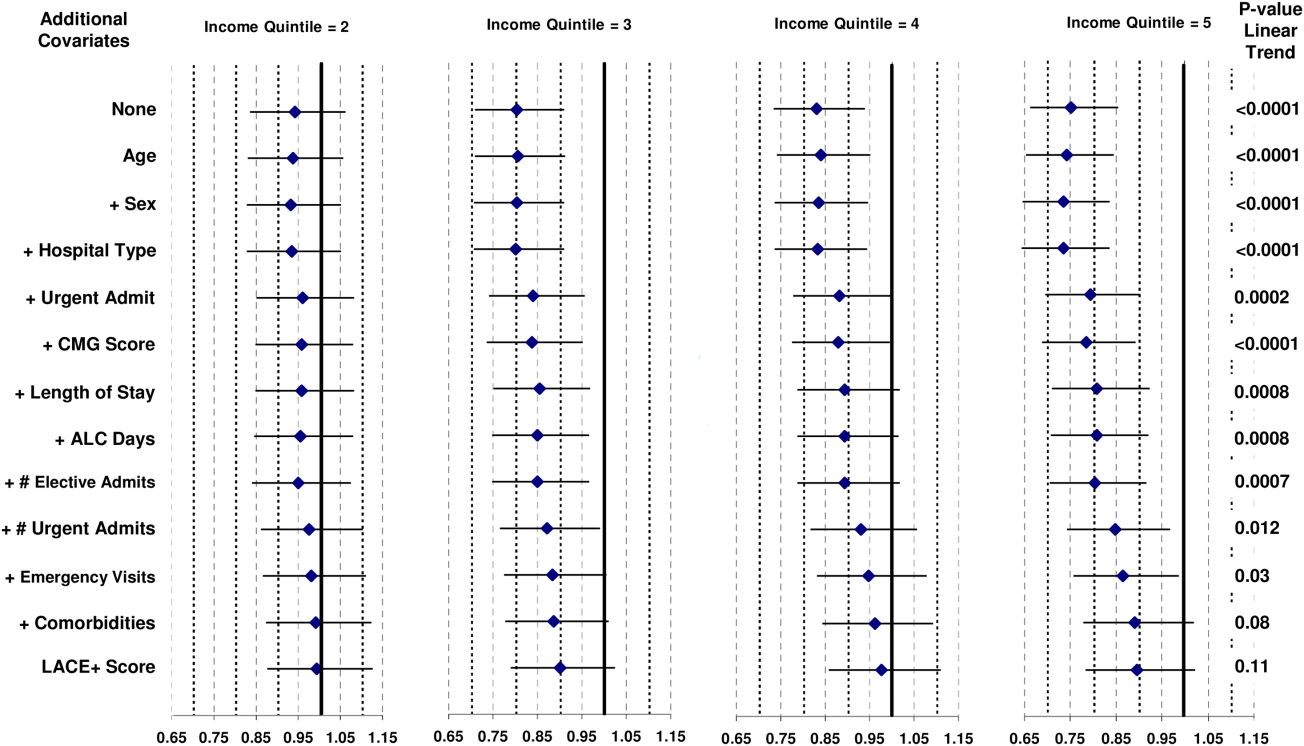
Patient and hospital covariates importantly influenced the daily conditional probability of discharge (Figure 1). Patients admitted to the obstetrics/gynecology department were notably more likely to be discharged from hospital with no influence from the day of week. In contrast, the probability of discharge decreased notably on the weekends in the other departments. Patients on the ward were much more likely to be discharged than those in the intensive care unit, with increasing age associated with a decreased discharge likelihood in the former but not the latter patients. Finally, discharge probabilities varied only slightly between campuses at our hospital with discharge risk decreasing as severity of illness (as measured by LAPS) increased.
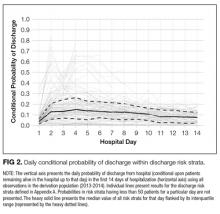
The TEND model contained 142 discharge risk strata (Appendix A). Weekend-holiday status had the strongest association with discharge probability (ie, it was the first splitting variable). The most complex discharge risk strata contained 6 covariates. The daily conditional probability of discharge during the first 2 weeks of hospitalization varied extensively between discharge risk strata (Figure 2). Overall, the conditional discharge probability increased from the first to the second day, remained relatively stable for several days, and then slowly decreased over time. However, this pattern and day-to-day variability differed extensively between risk strata.
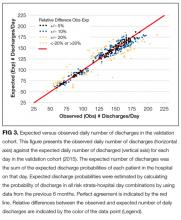
The observed daily number of discharges in the validation cohort varied extensively (median 139; interquartile range [IQR] 95-160; range 39-214). The TEND model accurately predicted the daily number of discharges with the expected daily number being strongly associated with the observed number (adjusted R2 = 89.2%; P < 0.0001; Figure 3). Calibration decreased but remained significant when we limited the analyses by hospital campus (General: R2 = 46.3%; P < 0.0001; Civic: R2 = 47.9%; P < 0.0001; Heart Institute: R2 = 18.1%; P < 0.0001). The expected number of daily discharges was an unbiased estimator of the observed number of discharges (its parameter estimate in a linear regression model with the observed number of discharges as the outcome variable was 1.0005; 95% confidence interval, 0.9647-1.0363). The absolute difference in the observed and expected daily number of discharges was small (median 1.6; IQR −6.8 to 9.4; range −37 to 63.4) as was the relative difference (median 1.4%; IQR −5.5% to 7.1%; range −40.9% to 43.4%). The expected number of discharges was within 20% of the observed number of discharges in 95.1% of days in 2015.
DISCUSSION
Knowing how many patients will soon be discharged from the hospital should greatly facilitate hospital planning. This study showed that the TEND model used simple patient and hospitalization covariates to accurately predict the number of patients who will be discharged from hospital in the next day.
We believe that this study has several notable findings. First, we think that using a nonparametric approach to predicting the daily number of discharges importantly increased accuracy. This approach allowed us to generate expected likelihoods based on actual discharge probabilities at our hospital in the most recent 6 months of hospitalization-days within patients having discharge patterns that were very similar to the patient in question (ie, discharge risk strata, Appendix A). This ensured that trends in hospitalization habits were accounted for without the need of a period variable in our model. In addition, the lack of parameters in the model will make it easier to transplant it to other hospitals. Second, we think that the accuracy of the predictions were remarkable given the relative “crudeness” of our predictors. By using relatively simple factors, the TEND model was able to output accurate predictions for the number of daily discharges (Figure 3).
This study joins several others that have attempted to accomplish the difficult task of predicting the number of hospital discharges by using digitized data. Barnes et al.11 created a model using regression random forest methods in a single medical service within a hospital to predict the daily number of discharges with impressive accuracy (mean daily number of discharges observed 8.29, expected 8.51). Interestingly, the model in this study was more accurate at predicting discharge likelihood than physicians. Levin et al.12 derived a model using discrete time logistic regression to predict the likelihood of discharge from a pediatric intensive care unit, finding that physician orders (captured via electronic order entry) could be categorized and used to significantly increase the accuracy of discharge likelihood. This study demonstrates the potential opportunities within health-related data from hospital data warehouses to improve prediction. We believe that continued work in this field will result in the increased use of digital data to help hospital administrators manage patient beds more efficiently and effectively than currently used resource intensive manual methods.13,14
Several issues should be kept in mind when interpreting our findings. First, our analysis is limited to a single institution in Canada. It will be important to determine if the TEND model methodology generalizes to other hospitals in different jurisdictions. Such an external validation, especially in multiple hospitals, will be important to show that the TEND model methodology works in other facilities. Hospitals could implement the TEND model if they are able to record daily values for each of the variables required to assign patients to a discharge risk stratum (Appendix A) and calculate within each the daily probability of discharge. Hospitals could derive their own discharge risk strata to account for covariates, which we did not include in our study but could be influential, such as insurance status. These discharge risk estimates could also be incorporated into the electronic medical record or hospital dashboards (as long as the data required to generate the estimates are available). These interventions would permit the expected number of hospital discharges (and even the patient-level probability of discharge) to be calculated on a daily basis. Second, 2 potential biases could have influenced the identification of our discharge risk strata (Appendix A). In this process, we used survival tree methods to separate patient-days into clusters having progressively more homogenous discharge patterns. Each split was determined by using a proportional hazards model that ignored the competing risks of death in hospital. In addition, the model expressed age and LAPS as continuous variables, whereas these covariates had to be categorized to create our risk strata groupings. The strength of a covariate’s association with an outcome will decrease when a continuous variable is categorized.15 Both of these issues might have biased our final risk strata categorization (Appendix A). Third, we limited our model to include simple covariates whose values could be determined relatively easily within most hospital administrative data systems. While this increases the generalizability to other hospital information systems, we believe that the introduction of other covariates to the model—such as daily vital signs, laboratory results, medications, or time from operations—could increase prediction accuracy. Finally, it is uncertain whether or not knowing the predicted number of discharges will improve the efficiency of bed management within the hospital. It seems logical that an accurate prediction of the number of beds that will be made available in the next day should improve decisions regarding the number of patients who could be admitted electively to the hospital. It remains to be seen, however, whether this truly happens.
In summary, we found that the TEND model used a handful of patient and hospitalization factors to accurately predict the expected number of discharges from hospital in the next day. Further work is required to implement this model into our institution’s data warehouse and then determine whether this prediction will improve the efficiency of bed management at our hospital.
Disclosure: CvW is supported by a University of Ottawa Department of Medicine Clinician Scientist Chair. The authors have no conflicts of interest
1. Austin PC, Rothwell DM, Tu JV. A comparison of statistical modeling strategies for analyzing length of stay after CABG surgery. Health Serv Outcomes Res Methodol. 2002;3:107-133.
2. Moran JL, Solomon PJ. A review of statistical estimators for risk-adjusted length of stay: analysis of the Australian and new Zealand intensive care adult patient data-base, 2008-2009. BMC Med Res Methodol. 2012;12:68. PubMed
3. Verburg IWM, de Keizer NF, de Jonge E, Peek N. Comparison of regression methods for modeling intensive care length of stay. PLoS One. 2014;9:e109684. PubMed
4. Beyersmann J, Schumacher M. Time-dependent covariates in the proportional subdistribution hazards model for competing risks. Biostatistics. 2008;9:765-776. PubMed
5. Latouche A, Porcher R, Chevret S. A note on including time-dependent covariate in regression model for competing risks data. Biom J. 2005;47:807-814. PubMed
6. Fitzmaurice GM, Laird NM, Ware JH. Marginal models: generalized estimating equations. Applied Longitudinal Analysis. 2nd ed. John Wiley & Sons; 2011;353-394.
7. Escobar GJ, Greene JD, Scheirer P, Gardner MN, Draper D, Kipnis P. Risk-adjusting hospital inpatient mortality using automated inpatient, outpatient, and laboratory databases. Med Care. 2008;46:232-239. PubMed
8. van Walraven C, Escobar GJ, Greene JD, Forster AJ. The Kaiser Permanente inpatient risk adjustment methodology was valid in an external patient population. J Clin Epidemiol. 2010;63:798-803. PubMed
9. Bou-Hamad I, Larocque D, Ben-Ameur H. A review of survival trees. Statist Surv. 2011;44-71.
10. van Walraven C, Bell CM. Risk of death or readmission among people discharged from hospital on Fridays. CMAJ. 2002;166:1672-1673. PubMed
11. Barnes S, Hamrock E, Toerper M, Siddiqui S, Levin S. Real-time prediction of inpatient length of stay for discharge prioritization. J Am Med Inform Assoc. 2016;23:e2-e10. PubMed
12. Levin SRP, Harley ETB, Fackler JCM, et al. Real-time forecasting of pediatric intensive care unit length of stay using computerized provider orders. Crit Care Med. 2012;40:3058-3064. PubMed
13. Resar R, Nolan K, Kaczynski D, Jensen K. Using real-time demand capacity management to improve hospitalwide patient flow. Jt Comm J Qual Patient Saf. 2011;37:217-227. PubMed
14. de Grood A, Blades K, Pendharkar SR. A review of discharge prediction processes in acute care hospitals. Healthc Policy. 2016;12:105-115. PubMed
15. van Walraven C, Hart RG. Leave ‘em alone - why continuous variables should be analyzed as such. Neuroepidemiology 2008;30:138-139. PubMed
Hospitals typically allocate beds based on historical patient volumes. If funding decreases, hospitals will usually try to maximize resource utilization by allocating beds to attain occupancies close to 100% for significant periods of time. This will invariably cause days in which hospital occupancy exceeds capacity, at which time critical entry points (such as the emergency department and operating room) will become blocked. This creates significant concerns over the patient quality of care.
Hospital administrators have very few options when hospital occupancy exceeds 100%. They could postpone admissions for “planned” cases, bring in additional staff to increase capacity, or instigate additional methods to increase hospital discharges such as expanding care resources in the community. All options are costly, bothersome, or cannot be actioned immediately. The need for these options could be minimized by enabling hospital administrators to make more informed decisions regarding hospital bed management by knowing the likely number of discharges in the next 24 hours.
Predicting the number of people who will be discharged in the next day can be approached in several ways. One approach would be to calculate each patient’s expected length of stay and then use the variation around that estimate to calculate each day’s discharge probability. Several studies have attempted to model hospital length of stay using a broad assortment of methodologies, but a mechanism to accurately predict this outcome has been elusive1,2 (with Verburg et al.3 concluding in their study’s abstract that “…it is difficult to predict length of stay…”). A second approach would be to use survival analysis methods to generate each patient’s hazard of discharge over time, which could be directly converted to an expected daily risk of discharge. However, this approach is complicated by the concurrent need to include time-dependent covariates and consider the competing risk of death in hospital, which can complicate survival modeling.4,5 A third approach would be the implementation of a longitudinal analysis using marginal models to predict the daily probability of discharge,6 but this method quickly overwhelms computer resources when large datasets are present.
In this study, we decided to use nonparametric models to predict the daily number of hospital discharges. We first identified patient groups with distinct discharge patterns. We then calculated the conditional daily discharge probability of patients in each of these groups. Finally, these conditional daily discharge probabilities were then summed for each hospital day to generate the expected number of discharges in the next 24 hours. This paper details the methods we used to create our model and the accuracy of its predictions.
METHODS
Study Setting and Databases Used for Analysis
The study took place at The Ottawa Hospital, a 1000-bed teaching hospital with 3 campuses that is the primary referral center in our region. The study was approved by our local research ethics board.
The Patient Registry Database records the date and time of admission for each patient (defined as the moment that a patient’s admission request is registered in the patient registration) and discharge (defined as the time when the patient’s discharge from hospital was entered into the patient registration) for hospital encounters. Emergency department encounters were also identified in the Patient Registry Database along with admission service, patient age and sex, and patient location throughout the admission. The Laboratory Database records all laboratory studies and results on all patients at the hospital.
Study Cohort
We used the Patient Registry Database to identify all people aged 1 year or more who were admitted to the hospital between January 1, 2013, and December 31, 2015. This time frame was selected to (i) ensure that data were complete; and (ii) complete calendar years of data were available for both derivation (patient-days in 2013-2014) and validation (2015) cohorts. Patients who were observed in the emergency room without admission to hospital were not included.
Study Outcome
The study outcome was the number of patients discharged from the hospital each day. For the analysis, the reference point for each day was 1 second past midnight; therefore, values for time-dependent covariates up to and including midnight were used to predict the number of discharges in the next 24 hours.
Study Covariates
Baseline (ie, time-independent) covariates included patient age and sex, admission service, hospital campus, whether or not the patient was admitted from the emergency department (all determined from the Patient Registry Database), and the Laboratory-based Acute Physiological Score (LAPS). The latter, which was calculated with the Laboratory Database using results for 14 tests (arterial pH, PaCO2, PaO2, anion gap, hematocrit, total white blood cell count, serum albumin, total bilirubin, creatinine, urea nitrogen, glucose, sodium, bicarbonate, and troponin I) measured in the 24-hour time frame preceding hospitalization, was derived by Escobar and colleagues7 to measure severity of illness and was subsequently validated in our hospital.8 The independent association of each laboratory perturbation with risk of death in hospital is reflected by the number of points assigned to each lab value with the total LAPS being the sum of these values. Time-dependent covariates included weekday in hospital and whether or not patients were in the intensive care unit.
Analysis
We used 3 stages to create a model to predict the daily expected number of discharges: we identified discharge risk strata containing patients having similar discharge patterns using data from patients in the derivation cohort (first stage); then, we generated the preliminary probability of discharge by determining the daily discharge probability in each discharge risk strata (second stage); finally, we modified the probability from the second stage based on the weekday and admission service and summed these probabilities to create the expected number of discharges on a particular date (third stage).
The first stage identified discharge risk strata based on the covariates listed above. This was determined by using a survival tree approach9 with proportional hazard regression models to generate the “splits.” These models were offered all covariates listed in the Study Covariates section. Admission service was clustered within 4 departments (obstetrics/gynecology, psychiatry, surgery, and medicine) and day of week was “binarized” into weekday/weekend-holiday (because the use of categorical variables with large numbers of groups can “stunt” regression trees due to small numbers of patients—and, therefore, statistical power—in each subgroup). The proportional hazards model identified the covariate having the strongest association with time to discharge (based on the Wald X2 value divided by the degrees of freedom). This variable was then used to split the cohort into subgroups (with continuous covariates being categorized into quartiles). The proportional hazards model was then repeated in each subgroup (with the previous splitting variable[s] excluded from the model). This process continued until no variable was associated with time to discharge with a P value less than .0001. This survival-tree was then used to cluster all patients into distinct discharge risk strata.
In the second stage, we generated the preliminary probability of discharge for a specific date. This was calculated by assigning all patients in hospital to their discharge risk strata (Appendix). We then measured the probability of discharge on each hospitalization day in all discharge risk strata using data from the previous 180 days (we only used the prior 180 days of data to account for temporal changes in hospital discharge patterns). For example, consider a 75-year-old patient on her third hospital day under obstetrics/gynecology on December 19, 2015 (a Saturday). This patient would be assigned to risk stratum #133 (Appendix A). We then measured the probability of discharge of all patients in this discharge risk stratum hospitalized in the previous 6 months (ie, between June 22, 2015, and December 18, 2015) on each hospital day. For risk stratum #133, the probability of discharge on hospital day 3 was 0.1111; therefore, our sample patient’s preliminary expected discharge probability was 0.1111.
To attain stable daily discharge probability estimates, a minimum of 50 patients per discharge risk stratum-hospitalization day combination was required. If there were less than 50 patients for a particular hospitalization day in a particular discharge risk stratum, we grouped hospitalization days in that risk stratum together until the minimum of 50 patients was collected.
The third (and final) stage accounted for the lack of granularity when we created the discharge risk strata in the first stage. As we mentioned above, admission service was clustered into 4 departments and the day of week was clustered into weekend/weekday. However, important variations in discharge probabilities could still exist within departments and between particular days of the week.10 Therefore, we created a correction factor to adjust the preliminary expected number of discharges based on the admission division and day of week. This correction factor used data from the 180 days prior to the analysis date within which the expected daily number of discharges was calculated (using the methods above). The correction factor was the relative difference between the observed and expected number of discharges within each division-day of week grouping.
For example, to calculate the correction factor for our sample patient presented above (75-year-old patient on hospital day 3 under gynecology on Saturday, December 19, 2015), we measured the observed number of discharges from gynecology on Saturdays between June 22, 2015, and December 18, 2015, (n = 206) and the expected number of discharges (n = 195.255) resulting in a correction factor of (observed-expected)/expected = (195.255-206)/195.206 = 0.05503. Therefore, the final expected discharge probability for our sample patient was 0.1111+0.1111*0.05503=0.1172. The expected number of discharges on a particular date was the preliminary expected number of discharges on that date (generated in the second stage) multiplied by the correction factor for the corresponding division-day or week group.
RESULTS
There were 192,859 admissions involving patients more than 1 year of age that spent at least part of their hospitalization between January 1, 2013, and December 31, 2015 (Table). Patients were middle-aged and slightly female predominant, with about half being admitted from the emergency department. Approximately 80% of admissions were to surgical or medical services. More than 95% of admissions ended with a discharge from the hospital with the remainder ending in a death. Almost 30% of hospitalization days occurred on weekends or holidays. Hospitalizations in the derivation (2013-2014) and validation (2015) group were essentially the same, except there was a slight drop in hospital length of stay (from a median of 4 days to 3 days) between the 2 periods.
Patient and hospital covariates importantly influenced the daily conditional probability of discharge (Figure 1). Patients admitted to the obstetrics/gynecology department were notably more likely to be discharged from hospital with no influence from the day of week. In contrast, the probability of discharge decreased notably on the weekends in the other departments. Patients on the ward were much more likely to be discharged than those in the intensive care unit, with increasing age associated with a decreased discharge likelihood in the former but not the latter patients. Finally, discharge probabilities varied only slightly between campuses at our hospital with discharge risk decreasing as severity of illness (as measured by LAPS) increased.
The TEND model contained 142 discharge risk strata (Appendix A). Weekend-holiday status had the strongest association with discharge probability (ie, it was the first splitting variable). The most complex discharge risk strata contained 6 covariates. The daily conditional probability of discharge during the first 2 weeks of hospitalization varied extensively between discharge risk strata (Figure 2). Overall, the conditional discharge probability increased from the first to the second day, remained relatively stable for several days, and then slowly decreased over time. However, this pattern and day-to-day variability differed extensively between risk strata.
The observed daily number of discharges in the validation cohort varied extensively (median 139; interquartile range [IQR] 95-160; range 39-214). The TEND model accurately predicted the daily number of discharges with the expected daily number being strongly associated with the observed number (adjusted R2 = 89.2%; P < 0.0001; Figure 3). Calibration decreased but remained significant when we limited the analyses by hospital campus (General: R2 = 46.3%; P < 0.0001; Civic: R2 = 47.9%; P < 0.0001; Heart Institute: R2 = 18.1%; P < 0.0001). The expected number of daily discharges was an unbiased estimator of the observed number of discharges (its parameter estimate in a linear regression model with the observed number of discharges as the outcome variable was 1.0005; 95% confidence interval, 0.9647-1.0363). The absolute difference in the observed and expected daily number of discharges was small (median 1.6; IQR −6.8 to 9.4; range −37 to 63.4) as was the relative difference (median 1.4%; IQR −5.5% to 7.1%; range −40.9% to 43.4%). The expected number of discharges was within 20% of the observed number of discharges in 95.1% of days in 2015.
DISCUSSION
Knowing how many patients will soon be discharged from the hospital should greatly facilitate hospital planning. This study showed that the TEND model used simple patient and hospitalization covariates to accurately predict the number of patients who will be discharged from hospital in the next day.
We believe that this study has several notable findings. First, we think that using a nonparametric approach to predicting the daily number of discharges importantly increased accuracy. This approach allowed us to generate expected likelihoods based on actual discharge probabilities at our hospital in the most recent 6 months of hospitalization-days within patients having discharge patterns that were very similar to the patient in question (ie, discharge risk strata, Appendix A). This ensured that trends in hospitalization habits were accounted for without the need of a period variable in our model. In addition, the lack of parameters in the model will make it easier to transplant it to other hospitals. Second, we think that the accuracy of the predictions were remarkable given the relative “crudeness” of our predictors. By using relatively simple factors, the TEND model was able to output accurate predictions for the number of daily discharges (Figure 3).
This study joins several others that have attempted to accomplish the difficult task of predicting the number of hospital discharges by using digitized data. Barnes et al.11 created a model using regression random forest methods in a single medical service within a hospital to predict the daily number of discharges with impressive accuracy (mean daily number of discharges observed 8.29, expected 8.51). Interestingly, the model in this study was more accurate at predicting discharge likelihood than physicians. Levin et al.12 derived a model using discrete time logistic regression to predict the likelihood of discharge from a pediatric intensive care unit, finding that physician orders (captured via electronic order entry) could be categorized and used to significantly increase the accuracy of discharge likelihood. This study demonstrates the potential opportunities within health-related data from hospital data warehouses to improve prediction. We believe that continued work in this field will result in the increased use of digital data to help hospital administrators manage patient beds more efficiently and effectively than currently used resource intensive manual methods.13,14
Several issues should be kept in mind when interpreting our findings. First, our analysis is limited to a single institution in Canada. It will be important to determine if the TEND model methodology generalizes to other hospitals in different jurisdictions. Such an external validation, especially in multiple hospitals, will be important to show that the TEND model methodology works in other facilities. Hospitals could implement the TEND model if they are able to record daily values for each of the variables required to assign patients to a discharge risk stratum (Appendix A) and calculate within each the daily probability of discharge. Hospitals could derive their own discharge risk strata to account for covariates, which we did not include in our study but could be influential, such as insurance status. These discharge risk estimates could also be incorporated into the electronic medical record or hospital dashboards (as long as the data required to generate the estimates are available). These interventions would permit the expected number of hospital discharges (and even the patient-level probability of discharge) to be calculated on a daily basis. Second, 2 potential biases could have influenced the identification of our discharge risk strata (Appendix A). In this process, we used survival tree methods to separate patient-days into clusters having progressively more homogenous discharge patterns. Each split was determined by using a proportional hazards model that ignored the competing risks of death in hospital. In addition, the model expressed age and LAPS as continuous variables, whereas these covariates had to be categorized to create our risk strata groupings. The strength of a covariate’s association with an outcome will decrease when a continuous variable is categorized.15 Both of these issues might have biased our final risk strata categorization (Appendix A). Third, we limited our model to include simple covariates whose values could be determined relatively easily within most hospital administrative data systems. While this increases the generalizability to other hospital information systems, we believe that the introduction of other covariates to the model—such as daily vital signs, laboratory results, medications, or time from operations—could increase prediction accuracy. Finally, it is uncertain whether or not knowing the predicted number of discharges will improve the efficiency of bed management within the hospital. It seems logical that an accurate prediction of the number of beds that will be made available in the next day should improve decisions regarding the number of patients who could be admitted electively to the hospital. It remains to be seen, however, whether this truly happens.
In summary, we found that the TEND model used a handful of patient and hospitalization factors to accurately predict the expected number of discharges from hospital in the next day. Further work is required to implement this model into our institution’s data warehouse and then determine whether this prediction will improve the efficiency of bed management at our hospital.
Disclosure: CvW is supported by a University of Ottawa Department of Medicine Clinician Scientist Chair. The authors have no conflicts of interest
Hospitals typically allocate beds based on historical patient volumes. If funding decreases, hospitals will usually try to maximize resource utilization by allocating beds to attain occupancies close to 100% for significant periods of time. This will invariably cause days in which hospital occupancy exceeds capacity, at which time critical entry points (such as the emergency department and operating room) will become blocked. This creates significant concerns over the patient quality of care.
Hospital administrators have very few options when hospital occupancy exceeds 100%. They could postpone admissions for “planned” cases, bring in additional staff to increase capacity, or instigate additional methods to increase hospital discharges such as expanding care resources in the community. All options are costly, bothersome, or cannot be actioned immediately. The need for these options could be minimized by enabling hospital administrators to make more informed decisions regarding hospital bed management by knowing the likely number of discharges in the next 24 hours.
Predicting the number of people who will be discharged in the next day can be approached in several ways. One approach would be to calculate each patient’s expected length of stay and then use the variation around that estimate to calculate each day’s discharge probability. Several studies have attempted to model hospital length of stay using a broad assortment of methodologies, but a mechanism to accurately predict this outcome has been elusive1,2 (with Verburg et al.3 concluding in their study’s abstract that “…it is difficult to predict length of stay…”). A second approach would be to use survival analysis methods to generate each patient’s hazard of discharge over time, which could be directly converted to an expected daily risk of discharge. However, this approach is complicated by the concurrent need to include time-dependent covariates and consider the competing risk of death in hospital, which can complicate survival modeling.4,5 A third approach would be the implementation of a longitudinal analysis using marginal models to predict the daily probability of discharge,6 but this method quickly overwhelms computer resources when large datasets are present.
In this study, we decided to use nonparametric models to predict the daily number of hospital discharges. We first identified patient groups with distinct discharge patterns. We then calculated the conditional daily discharge probability of patients in each of these groups. Finally, these conditional daily discharge probabilities were then summed for each hospital day to generate the expected number of discharges in the next 24 hours. This paper details the methods we used to create our model and the accuracy of its predictions.
METHODS
Study Setting and Databases Used for Analysis
The study took place at The Ottawa Hospital, a 1000-bed teaching hospital with 3 campuses that is the primary referral center in our region. The study was approved by our local research ethics board.
The Patient Registry Database records the date and time of admission for each patient (defined as the moment that a patient’s admission request is registered in the patient registration) and discharge (defined as the time when the patient’s discharge from hospital was entered into the patient registration) for hospital encounters. Emergency department encounters were also identified in the Patient Registry Database along with admission service, patient age and sex, and patient location throughout the admission. The Laboratory Database records all laboratory studies and results on all patients at the hospital.
Study Cohort
We used the Patient Registry Database to identify all people aged 1 year or more who were admitted to the hospital between January 1, 2013, and December 31, 2015. This time frame was selected to (i) ensure that data were complete; and (ii) complete calendar years of data were available for both derivation (patient-days in 2013-2014) and validation (2015) cohorts. Patients who were observed in the emergency room without admission to hospital were not included.
Study Outcome
The study outcome was the number of patients discharged from the hospital each day. For the analysis, the reference point for each day was 1 second past midnight; therefore, values for time-dependent covariates up to and including midnight were used to predict the number of discharges in the next 24 hours.
Study Covariates
Baseline (ie, time-independent) covariates included patient age and sex, admission service, hospital campus, whether or not the patient was admitted from the emergency department (all determined from the Patient Registry Database), and the Laboratory-based Acute Physiological Score (LAPS). The latter, which was calculated with the Laboratory Database using results for 14 tests (arterial pH, PaCO2, PaO2, anion gap, hematocrit, total white blood cell count, serum albumin, total bilirubin, creatinine, urea nitrogen, glucose, sodium, bicarbonate, and troponin I) measured in the 24-hour time frame preceding hospitalization, was derived by Escobar and colleagues7 to measure severity of illness and was subsequently validated in our hospital.8 The independent association of each laboratory perturbation with risk of death in hospital is reflected by the number of points assigned to each lab value with the total LAPS being the sum of these values. Time-dependent covariates included weekday in hospital and whether or not patients were in the intensive care unit.
Analysis
We used 3 stages to create a model to predict the daily expected number of discharges: we identified discharge risk strata containing patients having similar discharge patterns using data from patients in the derivation cohort (first stage); then, we generated the preliminary probability of discharge by determining the daily discharge probability in each discharge risk strata (second stage); finally, we modified the probability from the second stage based on the weekday and admission service and summed these probabilities to create the expected number of discharges on a particular date (third stage).
The first stage identified discharge risk strata based on the covariates listed above. This was determined by using a survival tree approach9 with proportional hazard regression models to generate the “splits.” These models were offered all covariates listed in the Study Covariates section. Admission service was clustered within 4 departments (obstetrics/gynecology, psychiatry, surgery, and medicine) and day of week was “binarized” into weekday/weekend-holiday (because the use of categorical variables with large numbers of groups can “stunt” regression trees due to small numbers of patients—and, therefore, statistical power—in each subgroup). The proportional hazards model identified the covariate having the strongest association with time to discharge (based on the Wald X2 value divided by the degrees of freedom). This variable was then used to split the cohort into subgroups (with continuous covariates being categorized into quartiles). The proportional hazards model was then repeated in each subgroup (with the previous splitting variable[s] excluded from the model). This process continued until no variable was associated with time to discharge with a P value less than .0001. This survival-tree was then used to cluster all patients into distinct discharge risk strata.
In the second stage, we generated the preliminary probability of discharge for a specific date. This was calculated by assigning all patients in hospital to their discharge risk strata (Appendix). We then measured the probability of discharge on each hospitalization day in all discharge risk strata using data from the previous 180 days (we only used the prior 180 days of data to account for temporal changes in hospital discharge patterns). For example, consider a 75-year-old patient on her third hospital day under obstetrics/gynecology on December 19, 2015 (a Saturday). This patient would be assigned to risk stratum #133 (Appendix A). We then measured the probability of discharge of all patients in this discharge risk stratum hospitalized in the previous 6 months (ie, between June 22, 2015, and December 18, 2015) on each hospital day. For risk stratum #133, the probability of discharge on hospital day 3 was 0.1111; therefore, our sample patient’s preliminary expected discharge probability was 0.1111.
To attain stable daily discharge probability estimates, a minimum of 50 patients per discharge risk stratum-hospitalization day combination was required. If there were less than 50 patients for a particular hospitalization day in a particular discharge risk stratum, we grouped hospitalization days in that risk stratum together until the minimum of 50 patients was collected.
The third (and final) stage accounted for the lack of granularity when we created the discharge risk strata in the first stage. As we mentioned above, admission service was clustered into 4 departments and the day of week was clustered into weekend/weekday. However, important variations in discharge probabilities could still exist within departments and between particular days of the week.10 Therefore, we created a correction factor to adjust the preliminary expected number of discharges based on the admission division and day of week. This correction factor used data from the 180 days prior to the analysis date within which the expected daily number of discharges was calculated (using the methods above). The correction factor was the relative difference between the observed and expected number of discharges within each division-day of week grouping.
For example, to calculate the correction factor for our sample patient presented above (75-year-old patient on hospital day 3 under gynecology on Saturday, December 19, 2015), we measured the observed number of discharges from gynecology on Saturdays between June 22, 2015, and December 18, 2015, (n = 206) and the expected number of discharges (n = 195.255) resulting in a correction factor of (observed-expected)/expected = (195.255-206)/195.206 = 0.05503. Therefore, the final expected discharge probability for our sample patient was 0.1111+0.1111*0.05503=0.1172. The expected number of discharges on a particular date was the preliminary expected number of discharges on that date (generated in the second stage) multiplied by the correction factor for the corresponding division-day or week group.
RESULTS
There were 192,859 admissions involving patients more than 1 year of age that spent at least part of their hospitalization between January 1, 2013, and December 31, 2015 (Table). Patients were middle-aged and slightly female predominant, with about half being admitted from the emergency department. Approximately 80% of admissions were to surgical or medical services. More than 95% of admissions ended with a discharge from the hospital with the remainder ending in a death. Almost 30% of hospitalization days occurred on weekends or holidays. Hospitalizations in the derivation (2013-2014) and validation (2015) group were essentially the same, except there was a slight drop in hospital length of stay (from a median of 4 days to 3 days) between the 2 periods.
Patient and hospital covariates importantly influenced the daily conditional probability of discharge (Figure 1). Patients admitted to the obstetrics/gynecology department were notably more likely to be discharged from hospital with no influence from the day of week. In contrast, the probability of discharge decreased notably on the weekends in the other departments. Patients on the ward were much more likely to be discharged than those in the intensive care unit, with increasing age associated with a decreased discharge likelihood in the former but not the latter patients. Finally, discharge probabilities varied only slightly between campuses at our hospital with discharge risk decreasing as severity of illness (as measured by LAPS) increased.
The TEND model contained 142 discharge risk strata (Appendix A). Weekend-holiday status had the strongest association with discharge probability (ie, it was the first splitting variable). The most complex discharge risk strata contained 6 covariates. The daily conditional probability of discharge during the first 2 weeks of hospitalization varied extensively between discharge risk strata (Figure 2). Overall, the conditional discharge probability increased from the first to the second day, remained relatively stable for several days, and then slowly decreased over time. However, this pattern and day-to-day variability differed extensively between risk strata.
The observed daily number of discharges in the validation cohort varied extensively (median 139; interquartile range [IQR] 95-160; range 39-214). The TEND model accurately predicted the daily number of discharges with the expected daily number being strongly associated with the observed number (adjusted R2 = 89.2%; P < 0.0001; Figure 3). Calibration decreased but remained significant when we limited the analyses by hospital campus (General: R2 = 46.3%; P < 0.0001; Civic: R2 = 47.9%; P < 0.0001; Heart Institute: R2 = 18.1%; P < 0.0001). The expected number of daily discharges was an unbiased estimator of the observed number of discharges (its parameter estimate in a linear regression model with the observed number of discharges as the outcome variable was 1.0005; 95% confidence interval, 0.9647-1.0363). The absolute difference in the observed and expected daily number of discharges was small (median 1.6; IQR −6.8 to 9.4; range −37 to 63.4) as was the relative difference (median 1.4%; IQR −5.5% to 7.1%; range −40.9% to 43.4%). The expected number of discharges was within 20% of the observed number of discharges in 95.1% of days in 2015.
DISCUSSION
Knowing how many patients will soon be discharged from the hospital should greatly facilitate hospital planning. This study showed that the TEND model used simple patient and hospitalization covariates to accurately predict the number of patients who will be discharged from hospital in the next day.
We believe that this study has several notable findings. First, we think that using a nonparametric approach to predicting the daily number of discharges importantly increased accuracy. This approach allowed us to generate expected likelihoods based on actual discharge probabilities at our hospital in the most recent 6 months of hospitalization-days within patients having discharge patterns that were very similar to the patient in question (ie, discharge risk strata, Appendix A). This ensured that trends in hospitalization habits were accounted for without the need of a period variable in our model. In addition, the lack of parameters in the model will make it easier to transplant it to other hospitals. Second, we think that the accuracy of the predictions were remarkable given the relative “crudeness” of our predictors. By using relatively simple factors, the TEND model was able to output accurate predictions for the number of daily discharges (Figure 3).
This study joins several others that have attempted to accomplish the difficult task of predicting the number of hospital discharges by using digitized data. Barnes et al.11 created a model using regression random forest methods in a single medical service within a hospital to predict the daily number of discharges with impressive accuracy (mean daily number of discharges observed 8.29, expected 8.51). Interestingly, the model in this study was more accurate at predicting discharge likelihood than physicians. Levin et al.12 derived a model using discrete time logistic regression to predict the likelihood of discharge from a pediatric intensive care unit, finding that physician orders (captured via electronic order entry) could be categorized and used to significantly increase the accuracy of discharge likelihood. This study demonstrates the potential opportunities within health-related data from hospital data warehouses to improve prediction. We believe that continued work in this field will result in the increased use of digital data to help hospital administrators manage patient beds more efficiently and effectively than currently used resource intensive manual methods.13,14
Several issues should be kept in mind when interpreting our findings. First, our analysis is limited to a single institution in Canada. It will be important to determine if the TEND model methodology generalizes to other hospitals in different jurisdictions. Such an external validation, especially in multiple hospitals, will be important to show that the TEND model methodology works in other facilities. Hospitals could implement the TEND model if they are able to record daily values for each of the variables required to assign patients to a discharge risk stratum (Appendix A) and calculate within each the daily probability of discharge. Hospitals could derive their own discharge risk strata to account for covariates, which we did not include in our study but could be influential, such as insurance status. These discharge risk estimates could also be incorporated into the electronic medical record or hospital dashboards (as long as the data required to generate the estimates are available). These interventions would permit the expected number of hospital discharges (and even the patient-level probability of discharge) to be calculated on a daily basis. Second, 2 potential biases could have influenced the identification of our discharge risk strata (Appendix A). In this process, we used survival tree methods to separate patient-days into clusters having progressively more homogenous discharge patterns. Each split was determined by using a proportional hazards model that ignored the competing risks of death in hospital. In addition, the model expressed age and LAPS as continuous variables, whereas these covariates had to be categorized to create our risk strata groupings. The strength of a covariate’s association with an outcome will decrease when a continuous variable is categorized.15 Both of these issues might have biased our final risk strata categorization (Appendix A). Third, we limited our model to include simple covariates whose values could be determined relatively easily within most hospital administrative data systems. While this increases the generalizability to other hospital information systems, we believe that the introduction of other covariates to the model—such as daily vital signs, laboratory results, medications, or time from operations—could increase prediction accuracy. Finally, it is uncertain whether or not knowing the predicted number of discharges will improve the efficiency of bed management within the hospital. It seems logical that an accurate prediction of the number of beds that will be made available in the next day should improve decisions regarding the number of patients who could be admitted electively to the hospital. It remains to be seen, however, whether this truly happens.
In summary, we found that the TEND model used a handful of patient and hospitalization factors to accurately predict the expected number of discharges from hospital in the next day. Further work is required to implement this model into our institution’s data warehouse and then determine whether this prediction will improve the efficiency of bed management at our hospital.
Disclosure: CvW is supported by a University of Ottawa Department of Medicine Clinician Scientist Chair. The authors have no conflicts of interest
1. Austin PC, Rothwell DM, Tu JV. A comparison of statistical modeling strategies for analyzing length of stay after CABG surgery. Health Serv Outcomes Res Methodol. 2002;3:107-133.
2. Moran JL, Solomon PJ. A review of statistical estimators for risk-adjusted length of stay: analysis of the Australian and new Zealand intensive care adult patient data-base, 2008-2009. BMC Med Res Methodol. 2012;12:68. PubMed
3. Verburg IWM, de Keizer NF, de Jonge E, Peek N. Comparison of regression methods for modeling intensive care length of stay. PLoS One. 2014;9:e109684. PubMed
4. Beyersmann J, Schumacher M. Time-dependent covariates in the proportional subdistribution hazards model for competing risks. Biostatistics. 2008;9:765-776. PubMed
5. Latouche A, Porcher R, Chevret S. A note on including time-dependent covariate in regression model for competing risks data. Biom J. 2005;47:807-814. PubMed
6. Fitzmaurice GM, Laird NM, Ware JH. Marginal models: generalized estimating equations. Applied Longitudinal Analysis. 2nd ed. John Wiley & Sons; 2011;353-394.
7. Escobar GJ, Greene JD, Scheirer P, Gardner MN, Draper D, Kipnis P. Risk-adjusting hospital inpatient mortality using automated inpatient, outpatient, and laboratory databases. Med Care. 2008;46:232-239. PubMed
8. van Walraven C, Escobar GJ, Greene JD, Forster AJ. The Kaiser Permanente inpatient risk adjustment methodology was valid in an external patient population. J Clin Epidemiol. 2010;63:798-803. PubMed
9. Bou-Hamad I, Larocque D, Ben-Ameur H. A review of survival trees. Statist Surv. 2011;44-71.
10. van Walraven C, Bell CM. Risk of death or readmission among people discharged from hospital on Fridays. CMAJ. 2002;166:1672-1673. PubMed
11. Barnes S, Hamrock E, Toerper M, Siddiqui S, Levin S. Real-time prediction of inpatient length of stay for discharge prioritization. J Am Med Inform Assoc. 2016;23:e2-e10. PubMed
12. Levin SRP, Harley ETB, Fackler JCM, et al. Real-time forecasting of pediatric intensive care unit length of stay using computerized provider orders. Crit Care Med. 2012;40:3058-3064. PubMed
13. Resar R, Nolan K, Kaczynski D, Jensen K. Using real-time demand capacity management to improve hospitalwide patient flow. Jt Comm J Qual Patient Saf. 2011;37:217-227. PubMed
14. de Grood A, Blades K, Pendharkar SR. A review of discharge prediction processes in acute care hospitals. Healthc Policy. 2016;12:105-115. PubMed
15. van Walraven C, Hart RG. Leave ‘em alone - why continuous variables should be analyzed as such. Neuroepidemiology 2008;30:138-139. PubMed
1. Austin PC, Rothwell DM, Tu JV. A comparison of statistical modeling strategies for analyzing length of stay after CABG surgery. Health Serv Outcomes Res Methodol. 2002;3:107-133.
2. Moran JL, Solomon PJ. A review of statistical estimators for risk-adjusted length of stay: analysis of the Australian and new Zealand intensive care adult patient data-base, 2008-2009. BMC Med Res Methodol. 2012;12:68. PubMed
3. Verburg IWM, de Keizer NF, de Jonge E, Peek N. Comparison of regression methods for modeling intensive care length of stay. PLoS One. 2014;9:e109684. PubMed
4. Beyersmann J, Schumacher M. Time-dependent covariates in the proportional subdistribution hazards model for competing risks. Biostatistics. 2008;9:765-776. PubMed
5. Latouche A, Porcher R, Chevret S. A note on including time-dependent covariate in regression model for competing risks data. Biom J. 2005;47:807-814. PubMed
6. Fitzmaurice GM, Laird NM, Ware JH. Marginal models: generalized estimating equations. Applied Longitudinal Analysis. 2nd ed. John Wiley & Sons; 2011;353-394.
7. Escobar GJ, Greene JD, Scheirer P, Gardner MN, Draper D, Kipnis P. Risk-adjusting hospital inpatient mortality using automated inpatient, outpatient, and laboratory databases. Med Care. 2008;46:232-239. PubMed
8. van Walraven C, Escobar GJ, Greene JD, Forster AJ. The Kaiser Permanente inpatient risk adjustment methodology was valid in an external patient population. J Clin Epidemiol. 2010;63:798-803. PubMed
9. Bou-Hamad I, Larocque D, Ben-Ameur H. A review of survival trees. Statist Surv. 2011;44-71.
10. van Walraven C, Bell CM. Risk of death or readmission among people discharged from hospital on Fridays. CMAJ. 2002;166:1672-1673. PubMed
11. Barnes S, Hamrock E, Toerper M, Siddiqui S, Levin S. Real-time prediction of inpatient length of stay for discharge prioritization. J Am Med Inform Assoc. 2016;23:e2-e10. PubMed
12. Levin SRP, Harley ETB, Fackler JCM, et al. Real-time forecasting of pediatric intensive care unit length of stay using computerized provider orders. Crit Care Med. 2012;40:3058-3064. PubMed
13. Resar R, Nolan K, Kaczynski D, Jensen K. Using real-time demand capacity management to improve hospitalwide patient flow. Jt Comm J Qual Patient Saf. 2011;37:217-227. PubMed
14. de Grood A, Blades K, Pendharkar SR. A review of discharge prediction processes in acute care hospitals. Healthc Policy. 2016;12:105-115. PubMed
15. van Walraven C, Hart RG. Leave ‘em alone - why continuous variables should be analyzed as such. Neuroepidemiology 2008;30:138-139. PubMed
© 2018 Society of Hospital Medicine
Hyperglycemia and CV Complications
Hyperglycemia in hospitalized patients is frequently observed and is recognized as an important threat to the health of patients with varying levels of illness, independent of diabetes status.[1, 2, 3, 4] Previous studies have found that in‐hospital hyperglycemia is associated with higher short‐term mortality rates,[5, 6, 7] longer lengths of stay, and higher rates of admission to intensive care units.[4]
In‐hospital hyperglycemia may be the result of diabetes mellitus or stress associated with hospitalization. The mechanism of stress hyperglycemia differs from diabetic hyperglycemia and can occur independently of diabetes status.[8] Stress hyperglycemia is characterized by rapid onset of insulin resistance, which normally takes months or years in diabetes mellitus. It develops in association with or because of other stressor such as infection or inflammatory processes.[9]
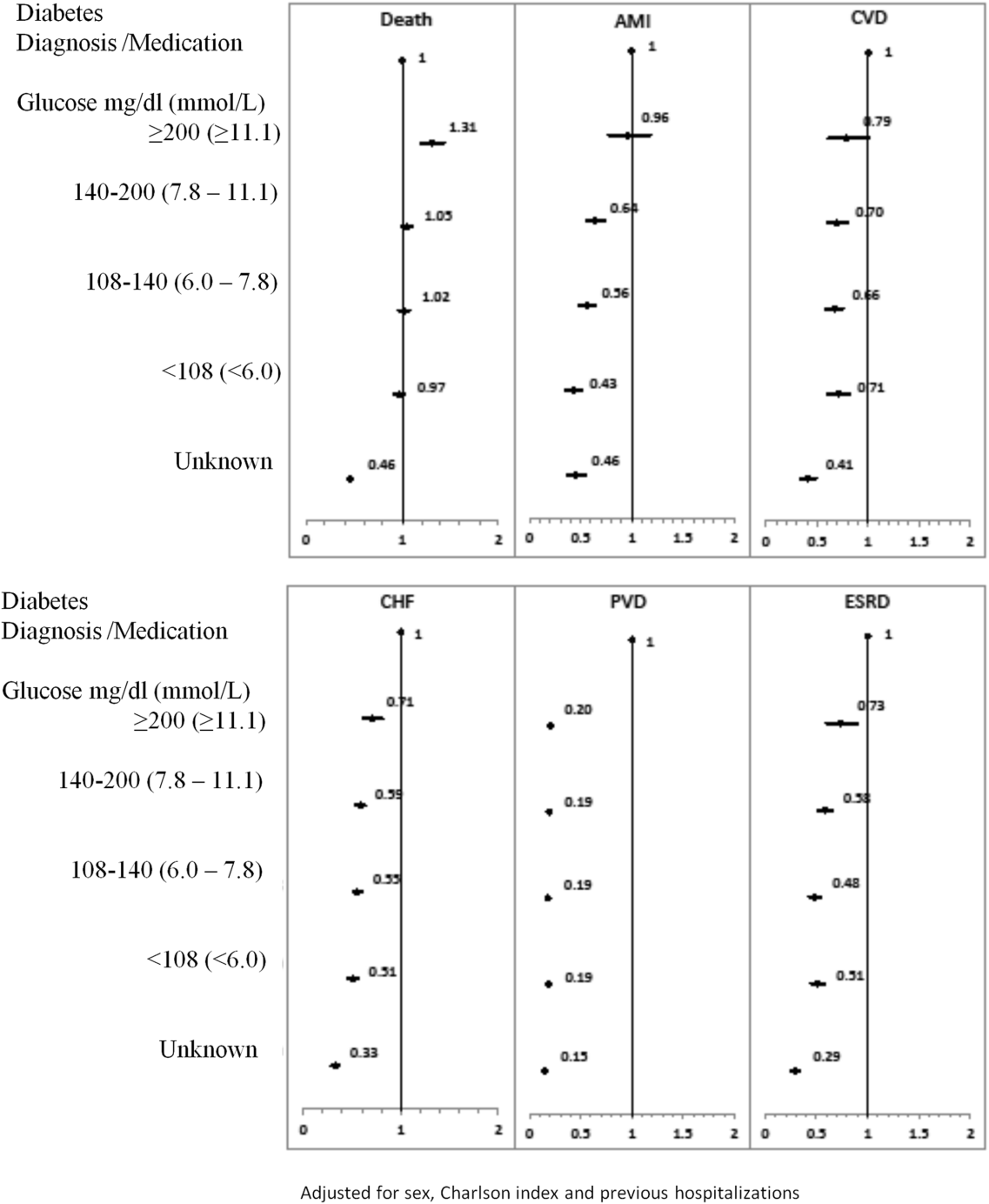
To our knowledge, no long‐term follow‐up study on hospitalized patients with elevated glucose levels but without a diabetes diagnosis has ever been conducted. In this study, we measured the 1‐ and 5‐year risk of mortality and diabetes‐related diseases for hospitalized patients with a diabetes diagnosis compared with patients grouped according to their peak in‐hospital serum glucose level. Our primary comparison was between patients with diagnosed diabetes and those with peak serum glucose >200 mg/dL (11.1 mmol/L), but we also examined 4 other categories of peak serum glucose: 140 to 200 mg/dL (7.811.1 mmol/L), 108 to 140 mg/dL (6.07.8 mmol/L), and <108 mg/dL (<6.0 mmol/L).
METHODS
Study Base
The study included all adult patients (excluding patients admitted to psychiatry and obstetrics) admitted to The Ottawa Hospital (TOH) between January 1, 1996 and March 31, 2008 and discharged alive. Included patients were 18 years or older and had complete medical record abstracts. TOH is the primary hospital in Ottawa, Ontario, Canada, and the main tertiary hospital in the Champlain Local Health Integration Network, the public healthcare authority for the Ottawa region. This study was approved by The Ottawa Hospital Research Ethics Board.
Data Sources
The Ottawa Hospital Data Warehouse (OHDW) is a repository for data from the hospital's patient information systems. These systems include patient registration information, discharge abstract, and laboratory, pharmacy, and radiology results. OHDW was used to determine each patient's age, gender, diagnoses, pharmacy orders, laboratory test results, in‐hospital comorbidities, most responsible hospital service, and admission urgency.
This dataset was linked to 3 population‐based administrative datasets and 1 derived cohort. Ontario's Registered Persons Database (RPDB) is a population‐based registry containing date of death (if applicable) as well as eligibility status for the provincial universal health insurance program, the Ontario Health Insurance Plan (OHIP).[10] The OHIP database records billing claims submitted by approximately 95% of Ontario physicians. Each claim contains a fee code describing the type of service provided and a location denoting where the service had taken place. The Canadian Institute for Health Information Discharge Abstract Database (DAD) records clinical, demographic, and administrative data for all hospital admissions and same‐day surgeries for all Ontario acute care hospitals since April 1, 1988. The Ontario Myocardial Infarction Database (OMID) contains records of all patients with a most responsible diagnosis of acute myocardial infarction (AMI) (International Classification of Diseases, 9th Revision [ICD‐9] code 410 or International Classification of Diseases, 10th Revision [ICD‐10] code I21) identified from the DAD. Details on the creation of the OMID are provided in an earlier study.[10]
Variable Definitions
We identified the index admission of the TOH cohort in the DAD using a unique encrypted health insurance number, admission and discharge dates, and the institution number. To avoid double counting, patients with the same encrypted health insurance number who were discharged from an institution and admitted to another within 2 days were classified as transfers and counted as 1 hospitalization.
Diabetes and cardiovascular (CV) complications (acute myocardial infarction [AMI], congestive heart failure [CHF], cardiovascular disease [CVD], peripheral vascular disease [PVD], and end‐stage renal disease [ESRD]) were identified in the discharge abstract as the most responsible diagnosis for the admission as well as postadmission comorbidities. The discharge abstract records diagnostic codes according to ICD‐9 (April 1, 1988March 31, 2002) or ICD‐10 (April 1, 2002March 1, 2009).
Each hospitalization was classified into 1 of 6 mutually exclusive diabetes status categories based on diagnostic codes, serum glucose test results, and pharmacy records. The diagnosed diabetes group included hospitalizations with any diagnostic code of diabetes in the discharge abstract or any order for a diabetes medication during hospitalization. Eligible medications included acarbose, acetohexamide, chlorpropamide, glibenclamide, gliclazide, glimepiride, glipizide, glyburide, insulin, metformin, nateglinide, pioglitazone, repaglinide, rosiglitazone, and tolbutamide. A chart validation study showed excellent ascertainment of diabetes status using these methods (correct classification 88.8%; 95% confidence interval [CI]: 85.791.3 with weighted kappa=0.89; 95% CI: 0.85‐0.92).[11, 12] Patients without diagnosed diabetes were classified according to their peak serum glucose value during the index hospitalization: <108 mg/dL (<6.0 mmol/L), 108 to 140 mg/dL (6.07.8 mmol/L), 140 to 200 mg/dL (7.811.1 mmol/L), >200 mg/dL (>11.1 mmol/L); hospitalizations in which glucose levels were not obtained were classified as unknown. These peak serum glucose categories are based on the World Health Organization's definition of diabetes and poor glucose tolerance.[12]
Outcomes
The primary outcome was all‐cause postdischarge mortality determined by linking the index admission to the RPDB. Secondary outcomes were CV complications, including: AMI (determined by linking to the OMID); hospitalization for CHF (determined by linking to the DAD for primary diagnosis of 425, 428, 514, 518.4 or I50, I42.0, I42.6, I42.7, I42.8, I42.9, I43, J81), CVD (determined by linking to the DAD for primary diagnosis of 430, 431, 432, 434, 436 or I60, I61, I62, I63, I64, G46), PVD (determined by primary diagnosis of 96.11, 96.12, 96.13, 96.14, 96.15 [excluded if in conjunction with 170, 171, 213, 730, 740759, 800900, 901904, 940950], 50.18, 51.25, 51.29 [excluded if in conjunction with 414.1, 441, 44] or 1VC93, 1VG93, 1VQ93, 1WA93, 1WE93, 1WJ93, 1WL93, 1WM93 [excluded if in conjunction with C40, C41, C46.1, C47, C49, D160, M46.2, M86, M87, M89.6, M90.0‐M90.5, Q00, Q38‐Q40, S02.0, S09.0, S04.0, S15, S25, T26), and 1KG50, 1KG57, 1KG76, 1KG35HAC1, 1KG35HHC1 [excluded if in conjunction with I60, I67.1, I71, I72, 177.0, 179.0]), and ESRD (determined by 403.9, 404.9,584, 585, 586, 788.5 or I12, I13, N17, N18, N19, R34).
Analysis
We identified all encounters of cohort patients in any Ontario acute‐care hospital within 5 years following the index discharge. Patients not covered by provincial health insurance (OHIP) were excluded.
We first measured crude mortality and morbidity rates by patient category (diagnosed diabetes and glucose levels). Next, we compared the unadjusted outcomes and baseline characteristics (age, sex, previous inpatient and emergency admissions, and disease at admission) between groups using a [2] test for categorical variables and analysis of variance for continuous variables.
Due to the violation of proportional hazards, we used the Weibull accelerated failure time model to calculate the hazard of death associated with diabetes status or serum glucose level. Consistency of the probability plots confirmed appropriateness of using the Weibull function. Competing risk is defined as a type of failure that prevents the observation of the event of interest or fundamentally alters the probability of its occurrence.[13, 14] In the comorbidity analyses, death is a competing risk for all other outcomes. We calculated the multivariate competing risk hazard for each outcome of interest except death. Each model was adjusted for potential confounders: baseline risk of in‐hospital mortality, common comorbidities, most responsible hospital service, and the number of previous inpatient admissions and emergency department visits to TOH in the previous 6 months. The probability of dying during the admission was calculated using the Escobar model, which predicts the in‐hospital probability of dying using data available at the time of admission to the hospital.[15] The Escobar model has been validated in the study population.[16] The baseline probability of dying was based on age, sex, acuity of admission, primary condition, Charlson comorbidity score,[17] and the laboratory‐based acute physiology score.[15] The Charlson comorbidity score was calculated using weights from Schneeweiss et al.[17] Kaplan‐Meier survival curves were created for both adjusted and unadjusted models. Death was used as the main censoring variable when analyzing nonfatal outcomes at 1‐ and 5‐year follow‐up.
Adjusted models were constructed using a stepwise selection technique and compared with Akaike and Bayesian information criteria values. For all tests, significance was defined as a P value of 0.05 or less.
We recognize that the cohort may contain more than 1 index hospitalization per patient. However, repeated analyses using only the first or last encounter per patient produced nearly identical hazard ratios (HRs) and CIs.
RESULTS
Between January 1, 1996 and March 31, 2008, 194,641 nonpsychiatric and nonobstetric adults were admitted to TOH. Seventeen patients were excluded because they were ineligible for healthcare coverage and had no encounter with the Ontario healthcare system following discharge from hospital, and 11,175 of the admissions ended in death. The final cohort consisted of 114,764 unique individuals representing 183,449 encounters.
Patients had a mean age of 59.5 years (standard deviation: 18.0) and 48.9% were male. The baseline risk of dying during hospitalization was 4.8%.
Table 1 describes patients by diabetes and peak serum glucose status. Patients with diagnosed diabetes were more likely to be older and male. Patients with elevated peak serum glucose (>200 mg/dL; >11.1 mmol/L) were younger than the diagnosed diabetes group and had a higher baseline probability of in‐hospital death (9.4%, 95% CI: 9.09.7). Patients in these 2 groups had more inpatient admissions within the previous 6 months compared to the groups with other peak serum glucose values.
| Serum Glucose Level, mg/dL | ||||||
|---|---|---|---|---|---|---|
| Diagnosed Diabetes, n=32,774, 17.9% | >200, n=5,082, 2.8% | 140200, n=25,857, 14.1% | 108140, n=38,741, 21.1% | <108, n=27,603, 15.0% | Unknown, n=53,392, 29.1% | |
| ||||||
| Age, y, mean (SD) | 65.8 (14.1) | 64.3 (17.0)a | 63.9 (17.3)a | 60.9 (18.6)a | 54.3 (19.7)a | 54.8 (16.9)a |
| Risk‐adjusted mortality at admission, mean (SD) | 0.08 (0.12) | 0.09 (0.12)a | 0.07 (0.10)a | 0.05 (0.09)a | 0.04 (0.07)a | 0.01 (0.04)a |
| Sex, male, no. (%) | 18,200 (55.5) | 2,610 (51.4)a | 13,477 (52.1)a | 19,495 (50.3)a | 12,907 (46.8)a | 22,951 (43.0)a |
| No. of previous inpatient admissions, 6 months (%) | ||||||
| 0 | 22,780 (69.5) | 3,576 (70.4) | 19,118 (73.9)a | 28,827 (74.4)a | 20,354 (73.7)a | 43,317 (81.1)a |
| 1 | 6,470 (19.7) | 962 (18.9) | 4,484 (17.3)a | 6,526 (16.9)a | 4,744 (17.2)a | 7,360 (13.8)a |
| 2+ | 3,524 (10.8) | 544 (10.7) | 2,255 (8.7)a | 3,388 (9.1)a | 2,505 (9.1)a | 2,715 (5.1)a |
| No. of previous emergency admissions (6 months) (%) | ||||||
| 0 | 15,518 (47.4) | 2,638 (51.9)a | 12,681 (49.0)a | 16,584 (42.8)a | 13,039 (47.2) | 43,112 (80.8)a |
| 1 | 9,665 (29.5) | 1,490 (29.3)a | 8,339 (32.3)a | 13,829 (35.7)a | 8,709 (31.6) | 6,533 (12.2)a |
| 2+ | 7,591 (23.2) | 954 (18.8)a | 4,837 (18.7)a | 8,328 (21.5)a | 5,855 (21.2) | 3,747 (7.0)a |
| Emergency admission at index hospitalization (%) | 25,420 (77.6) | 4,178 (82.2)a | 20,284 (78.5)a | 33,282 (85.9)a | 23,598 (85.5)a | 15,039 (28.2)a |
| Length of stay, d (mean/SD) | 12.4 (22.3) | 15.8 (30.0)a | 11.9 (17.1)a | 8.5 (12.2)a | 6.3 (9.5)a | 3.4 (4.9)a |
| Disease at index hospitalization (%) | ||||||
| PVD | 2,783 (8.5) | 257 (5.1)a | 1,387 (5.4)a | 1,372 (3.5)a | 908 (3.3)a | 965 (1.8)a |
| Pneumonia | 3,308 (10.1) | 658 (13.0)a | 2,577 (10.0) | 2,809 (7.3)a | 1,220 (4.4)a | 399 (0.8)a |
| UTI | 3,549 (10.8) | 665 (13.1)a | 2,660 (10.3)a | 3,336 (8.6)a | 1,559 (5.7)a | 929 (1.7)a |
| IHD | 8,957 (27.3) | 1,086 (21.4)a | 4,714 (18.2)a | 5,306 (13.7)a | 3,100 (11.2)a | 2,842 (5.3)a |
| Hypertension | 10,864 (33.2) | 1,115 (21.9)a | 5,155 (19.9)a | 5,880 (15.2)a | 3,045 (11.0)a | 3,211 (6.0)a |
| Arrhythmia | 5,010 (15.3) | 823 (16.2) | 3,768 (14.6)a | 3,718 (9.6)a | 2,046 (7.4)a | 1,172 (2.2)a |
| CHF | 570 (17.5) | 763 (15.0)a | 2,761 (10.7)a | 2,449 (6.3)a | 1,121 (4.1)a | 386 (0.7)a |
| Diagnoses of diabetes in the next year (%) | 126 (2.5) | 368 (1.4) | 370 (1.0) | 215 (0.8) | 540 (1.0) | |
| Diagnoses of diabetes in the next 5 years (%) | 310 (6.1) | 981 (3.8) | 916 (2.4) | 434 (1.7) | 1,317 (2.5) | |
| First 3 most common primary discharge codes | AHD I251 (5.7%), HF I50 (3.1%), NSTEMI I214 (1.6%) | AHD I251 (2.7%), COPD J441 (2.1%), HF I50 (2.0%) | AHD I251 (4.0%), Pneumonia J189 (1.6%), HF I50 (1.5%) | AHD I251 (1.6%), Pneumonia J189 (1.5%), CA D700 (1.3%) | AHD I251 (1.8%), AA K359 (1.7%), UA I200 (1.2%) | OA M171 (2.3%), AHD I251 (2.2%), OA M170 (1.7%) |
Of the 5082 patients classified with a peak serum glucose measurement >200 mg/dL (11.1 mmol/L), 15% had 2 and 8% had more than 2 serum glucose measurements that exceeded this threshold. For the remaining patients (with 1 peak serum glucose measurement >200 mg/dL), 52% had additional serum glucose measurements over 140 mg/dL (7.8 mmol/L).
Table 2 presents crude 1‐ and 5‐year mortality and morbidity rates by patient group. The mortality rate is the percentage of patients who died within 1 year and 5 years of their index admission, with or without developing a CV complication. Morbidity rate describes the percentage who developed the complication among patients who survived after discharge or developed the complication prior to death within a 1‐year and 5‐year period. During the 1‐year follow‐up period, the crude mortality rate among patients with elevated peak serum glucose was higher than all other groups (25.4% vs 20.6% for diagnosed diabetes and 7.4% to 22.5% for other peak serum glucose levels; all P<0.0001). For the 5‐year follow‐up, the gap between patients with elevated peak serum glucose and those with diagnosed diabetes lessened but remained significant (45.1% vs 41.7%; P<0.0001). In the 1‐year follow‐up, patients with diagnosed diabetes had significantly higher morbidity rates than all other groups except for AMI. The difference in the rate of AMI for diagnosed diabetes and patients with elevated glucose was not statistically significant.
| Diagnosed Diabetes, n=32,774 | Serum Glucose Level (mg/dL) | |||||
|---|---|---|---|---|---|---|
| >200, n=5,082 | 140200, n=25,857 | 108140, n=38,741 | <108, n=27,603 | Unknown, n=53,392 | ||
| ||||||
| All‐cause death | ||||||
| 1 year | 6,762 (20.6) | 1,293 (25.4)a | 5,309 (20.5) | 7,212 (18.6)a | 4,178 (15)a | 3,969 (7.4)a |
| 5 years | 13,659 (41.7) | 2,292 (45.1)a | 9,871 (38.2)a | 13,256 (34.2)a | 7,606 (27.6)a | 98,614 (16.1)a |
| AMI | ||||||
| 1 year | 728 (2.8) | 104 (2.7) | 326 (1.6)a | 386 (1.2)a | 172 (0.7)a | 218 (0.4)a |
| 5 years | 1,687 (8.4) | 182 (6.3)a | 687 (4.2)a | 837 (3.2)a | 436 (2.2)a | 633 (1.4)a |
| CVD | ||||||
| 1 year | 582 (2.2) | 71 (1.9) | 306 (1.5)a | 403 (1.3)a | 251 (1.1)a | 195 (0.4)a |
| 5 years | 1,153 (5.8) | 143 (5.0) | 623 (3.8)a | 872 (3.4)a | 470 (2.3)a | 534 (1.2)a |
| CHF | ||||||
| 1 year | 2,260 (8.4) | 245 (6.3)a | 870 (4.2)a | 1,023 (3.2)a | 516 (2.2)a | 362 (0.7)a |
| 5 years | 3,830 (17.7) | 395 (12.9)a | 1,529 (9.0)a | 1,802 (6.8)a | 960 (4.7)a | 884 (2.0)a |
| PVD | ||||||
| 1 year | 795 (3.0) | 24 (0.6)a | 114 (0.6)a | 154 (0.5)a | 97 (0.4)a | 141 (0.3)a |
| 5 years | 1,547 (7.8) | 50 (1.8)a | 220 (1.4)a | 275 (1.1)a | 192 (1.0)a | 295 (0.7)a |
| ESRD | ||||||
| 1 year | 953 (3.6) | 104 (2.7)a | 403 (1.9)a | 457 (1.4)a | 311 (1.3)a | 329 (0.7)a |
| 5 years | 1,938 (9.5) | 183 (6.3)a | 807 (4.9)a | 995 (3.8)a | 611 (3.0)a | 771 (1.7)a |
The 1‐year adjusted hazard ratios for mortality and CV complications are presented in Figure 1. After adjustment for baseline demographics and clinical and hospital factors, having a peak serum glucose level above 200 mg/dL (11.1 mmol/L) was an independent predictor of death. The mortality risk for this group in the year following discharge was 31% higher than patients with diagnosed diabetes (adjusted HR: 1.31, 95% CI: 1.20‐1.43). There was no mortality risk difference between the group with diagnosed diabetes and the lower peak serum glucose levels (adjusted HR: 1.05, 95% CI: 0.99‐1.11), 108160 mg/dL (6.07.8 mmol/L) (adjusted HR: 1.02, 95% CI: 0.971.07); and <108 mg/dL (<6.0 mmol/L) (adjusted HR: 0.97, 95% CI: 0.921.03). Adjusted HRs, with 95% CIs and P values for 5‐year follow‐up are presented in Figure 2.
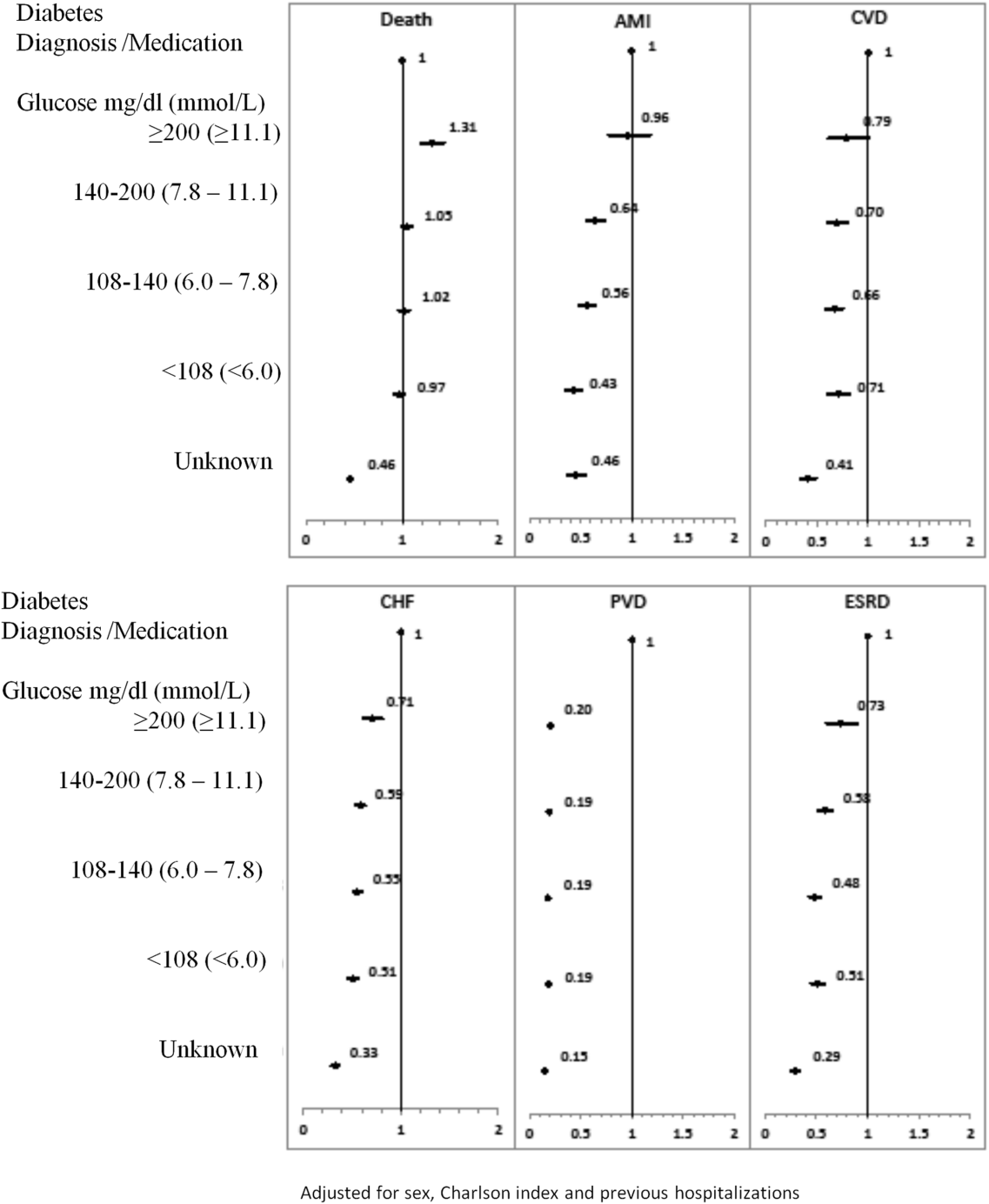
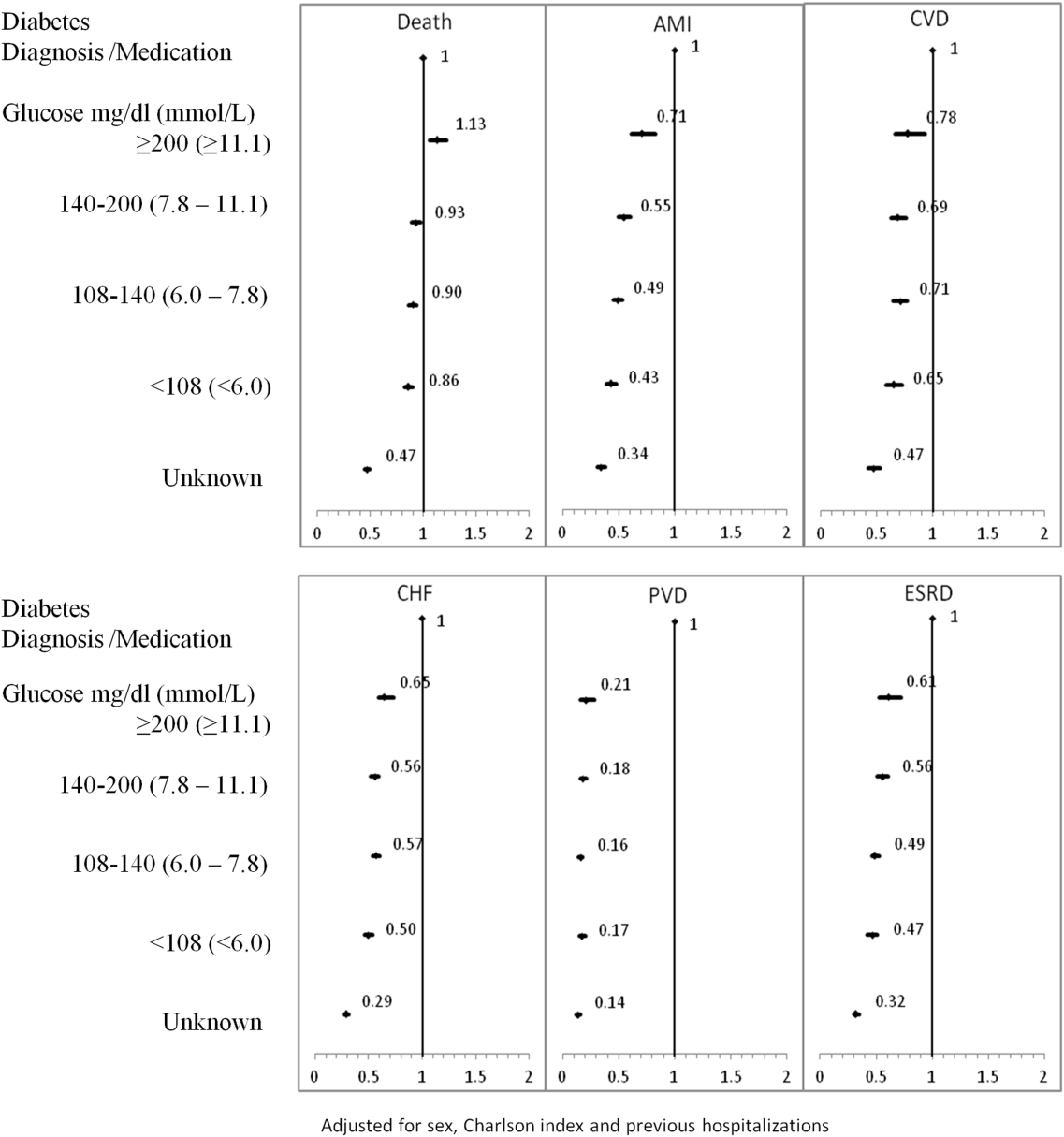
Adjusted hazard ratios for morbidity showed a different pattern. Patients with diagnosed diabetes had a higher risk of developing complications in the year following discharge from the hospital (Figure 1). After adjusting for potential confounders, we found that patients with diagnosed diabetes had the same risk of AMI and CVD as patients with peak serum glucose levels above 200 mg/dL (11.1 mmol/L) (AMI, adjusted HR: 0.96; 95% CI: 0.78‐1.18; CVD, adjusted HR: 0.79; 95% CI: 0.61‐1.00) but a 36% to 57% higher AMI risk and 29% to 34% higher CVD risk than other peak serum glucose level groups. Compared to all peak serum glucose groups, patients with diagnosed diabetes had a significantly higher risk of developing CHF, PVD, and ESRD (Figure 1). Similarly, the 5‐year risk of AMI, CVD, CHF, PVD, and ESRD was higher for patients with diagnosed diabetes compared to all peak serum glucose groups (Figure 2).
CONCLUSION/DISCUSSION
The study found that in‐hospital hyperglycemia was a strong predictor of mortality at 1‐ and 5‐years follow‐up, even after adjustment using well‐established and discriminating comorbidity measures. Extreme in‐hospital hyperglycemia was a stronger predictor of mortality than diagnosed diabetes.
Previous studies have shown that diabetes and stress hyperglycemia among hospitalized patients are important markers for poor clinical outcomes and in‐hospital mortality.[1, 2, 4] This study indicates that hospitalized patients with extreme hyperglycemia (peak serum glucose >200 mg/dL) were at a high risk of death for at least 5 years following discharge.
These findings, based on a large general sample of hospitalized patients, indicate that the extreme elevations in peak serum glucose convey a risk for all hospitalized patients, not only those with critical illness.[3, 18] Hyperglycemia appears to be an independent indicator of mortality risk and should be evaluated as a potential component within risk prediction tools. Further study is required to determine mechanisms for this risk association to identify what therapies, if any, might be used to minimize this risk.
The diagnosed diabetes group, which likely included some patients who also had extreme in‐hospital hyperglycemia, had a lower 1‐year risk of death than patients with hyperglycemia who did not have diabetes diagnosis. This may be an indication of the protective effect of blood glucose control, because patients with diabetes are more likely to receive therapy for hyperglycemia during and after hospitalization.
Classification of patients by several serum glucose levels (as opposed to a dichotomous classification, where hyperglycemia is either present or absent), showed that hyperglycemia constitutes a graded risk[5] for almost all outcomes examined, particularly mortality, AMI, and CVD.
Previous studies indicate that diabetes is observed in only 23% to 35% of hospitalized patients with hyperglycemia.[18, 19] We would expect higher risk for CV complications for patients with elevated glucose if the proportion of these patients who had undiagnosed diabetes was higher than the proportion estimated in the literature. However, we observed lower risk of CV complications (especially PVD and ESRD) for the elevated glucose group in the 1 and 5 years following discharge. In‐hospital hyperglycemia is not equivalent to undiagnosed diabetes.
There are several potential limitations in this study. The first is our method for ascertaining CV complications. Diverse disease definitions are used in medical literature, and similar studies using different definitions may yield different results, though we would not expect to find a wide range of variation. Second, our study did not include information about severity of diabetes and the persistence of elevated glucose; if available, this knowledge may provide better insight into patient experiences, especially in long‐term follow‐up. Third, results are also limited by the absence of data on cause of death, a potentially helpful means of identifying posthospitalization difficulties experienced by patients with hyperglycemia. Fourth, this study mainly compares experiences of patients with elevated peak serum glucose level to diabetes patients; it would be worthwhile to explore the impact of lower gradations of glucose levels.
We would like to emphasize that we did not confirm diabetes diagnosis following discharge for patients with hyperglycemia. However, we did not observe a high rate of complications at 5‐year follow‐up, particularly for ESRD. This may be because most patients with in‐hospital elevated glucose had early diabetes or transient hyperglycemia and therefore lower risk of long‐term diabetes‐specific consultations.
Hyperglycemia is an important independent indicator, carrying a greater risk for 1‐ and 5‐year mortality than diagnosed diabetes. However, it is unclear whether hospitalized patients with elevated peak serum glucose have early diabetes or their hyperglycemia reflects hospital stress or another comorbidity concept.
Acknowledgements
The authors are grateful to Amy Zierler and Allison Whalen O'Connor for their editorial assistance. This study was supported by the Institute for Clinical Evaluative Sciences (ICES), which is funded by an annual grant from the Ontario Ministry of Health and Long‐Term Care (MOHLTC). The opinions, results and conclusions reported in this paper are those of the authors and are independent from the funding sources. No endorsement by ICES or the Ontario MOHLTC is intended or should be inferred.
Disclosure: Nothing to report.
- , , , et al. Management of diabetes and hyperglycemia in hospitals. Diabetes Care. 2004;27(2):553–591.
- , , , et al. American Association of Clinical Endocrinologists and American Diabetes Association consensus statement on inpatient glycemic control. Diabetes Care. 2009;32(6):1119–1131.
- The NICE‐SUGAR Study Investigators. Intensive versus conventional glucose control in critically ill patients. N Engl J Med. 2009;360(13):1283–1297.
- , , , , , . Hyperglycemia: an independent marker of in‐hospital mortality in patients with undiagnosed diabetes. J Clin Endocrinol Metab. 2002;87(3):978–982.
- , , , , . Hyperglycemia‐related mortality in critically ill patients varies with admission diagnosis. Crit Care Med. 2009;37(12):3001–3009.
- , . Hospital management of hyperglycemia. Curr Opin Endocrinol Diabetes Obes. 2011;18(2):110–118.
- , , , et al. IScore: a risk score to predict death early after hospitalization for an acute ischemic stroke. Circulation. 2011;123(7):739–749.
- , . Does Stress‐induced hyperglycemia increase the risk of perioperative infectious complications in orthopaedic trauma patients? J Orthop Trauma. 2010;24(12):752–756.
- . Metabolic mechanisms of stress hyperglycemia. J Parenter Enteral Nutr. 2006;30(2):157–163.
- , , . Temporal changes in the outcomes of acute myocardial infarction in Ontario, 1992–1996. CMAJ. 1999;161(10):1257–1261.
- , , , et al. The accuracy of using integrated electronic health care data to identify patients with undiagnosed diabetes mellitus. J Eval Clin Pract. 2012;18(3):606–611.
- American Diabetes Association. Diagnosis and classification of diabetes mellitus. Diabetes Care. 2006;29(suppl 1):s43–s48.
- . Dealing with competing risks: testing covariates and calculating sample size. Stat Med. 2002;21(22):3317–3324.
- , , , . Competing risk analysis of events 10 years after revascularization. Scand Cardiovasc J. 2010;44(5):279–288.
- , , , , , . Risk‐adjusting hospital inpatient mortality using automated inpatient, outpatient, and laboratory databases. Med Care. 2008;46(3):232–239.
- , , , . The Kaiser Permanente inpatient risk adjustment methodology was valid in an external patient population. J Clin Epidemiol. 2010;63(7):798–803.
- , , , . Improved comorbidity adjustment for predicting mortality in medicare populations. Health Serv Res. 2003;38(4):1103–1120.
- , , , et al. Glucose metabolism in patients with acute myocardial infarction and no previous diagnosis of diabetes mellitus: a prospective study. Lancet. 2002;359(9324):2140–2144.
- , , , et al. Disorders of glucose metabolism in acute stroke patients: an underrecognized problem. Diabetes Care. 2006;29(4):792–797.
Hyperglycemia in hospitalized patients is frequently observed and is recognized as an important threat to the health of patients with varying levels of illness, independent of diabetes status.[1, 2, 3, 4] Previous studies have found that in‐hospital hyperglycemia is associated with higher short‐term mortality rates,[5, 6, 7] longer lengths of stay, and higher rates of admission to intensive care units.[4]
In‐hospital hyperglycemia may be the result of diabetes mellitus or stress associated with hospitalization. The mechanism of stress hyperglycemia differs from diabetic hyperglycemia and can occur independently of diabetes status.[8] Stress hyperglycemia is characterized by rapid onset of insulin resistance, which normally takes months or years in diabetes mellitus. It develops in association with or because of other stressor such as infection or inflammatory processes.[9]
To our knowledge, no long‐term follow‐up study on hospitalized patients with elevated glucose levels but without a diabetes diagnosis has ever been conducted. In this study, we measured the 1‐ and 5‐year risk of mortality and diabetes‐related diseases for hospitalized patients with a diabetes diagnosis compared with patients grouped according to their peak in‐hospital serum glucose level. Our primary comparison was between patients with diagnosed diabetes and those with peak serum glucose >200 mg/dL (11.1 mmol/L), but we also examined 4 other categories of peak serum glucose: 140 to 200 mg/dL (7.811.1 mmol/L), 108 to 140 mg/dL (6.07.8 mmol/L), and <108 mg/dL (<6.0 mmol/L).
METHODS
Study Base
The study included all adult patients (excluding patients admitted to psychiatry and obstetrics) admitted to The Ottawa Hospital (TOH) between January 1, 1996 and March 31, 2008 and discharged alive. Included patients were 18 years or older and had complete medical record abstracts. TOH is the primary hospital in Ottawa, Ontario, Canada, and the main tertiary hospital in the Champlain Local Health Integration Network, the public healthcare authority for the Ottawa region. This study was approved by The Ottawa Hospital Research Ethics Board.
Data Sources
The Ottawa Hospital Data Warehouse (OHDW) is a repository for data from the hospital's patient information systems. These systems include patient registration information, discharge abstract, and laboratory, pharmacy, and radiology results. OHDW was used to determine each patient's age, gender, diagnoses, pharmacy orders, laboratory test results, in‐hospital comorbidities, most responsible hospital service, and admission urgency.
This dataset was linked to 3 population‐based administrative datasets and 1 derived cohort. Ontario's Registered Persons Database (RPDB) is a population‐based registry containing date of death (if applicable) as well as eligibility status for the provincial universal health insurance program, the Ontario Health Insurance Plan (OHIP).[10] The OHIP database records billing claims submitted by approximately 95% of Ontario physicians. Each claim contains a fee code describing the type of service provided and a location denoting where the service had taken place. The Canadian Institute for Health Information Discharge Abstract Database (DAD) records clinical, demographic, and administrative data for all hospital admissions and same‐day surgeries for all Ontario acute care hospitals since April 1, 1988. The Ontario Myocardial Infarction Database (OMID) contains records of all patients with a most responsible diagnosis of acute myocardial infarction (AMI) (International Classification of Diseases, 9th Revision [ICD‐9] code 410 or International Classification of Diseases, 10th Revision [ICD‐10] code I21) identified from the DAD. Details on the creation of the OMID are provided in an earlier study.[10]
Variable Definitions
We identified the index admission of the TOH cohort in the DAD using a unique encrypted health insurance number, admission and discharge dates, and the institution number. To avoid double counting, patients with the same encrypted health insurance number who were discharged from an institution and admitted to another within 2 days were classified as transfers and counted as 1 hospitalization.
Diabetes and cardiovascular (CV) complications (acute myocardial infarction [AMI], congestive heart failure [CHF], cardiovascular disease [CVD], peripheral vascular disease [PVD], and end‐stage renal disease [ESRD]) were identified in the discharge abstract as the most responsible diagnosis for the admission as well as postadmission comorbidities. The discharge abstract records diagnostic codes according to ICD‐9 (April 1, 1988March 31, 2002) or ICD‐10 (April 1, 2002March 1, 2009).
Each hospitalization was classified into 1 of 6 mutually exclusive diabetes status categories based on diagnostic codes, serum glucose test results, and pharmacy records. The diagnosed diabetes group included hospitalizations with any diagnostic code of diabetes in the discharge abstract or any order for a diabetes medication during hospitalization. Eligible medications included acarbose, acetohexamide, chlorpropamide, glibenclamide, gliclazide, glimepiride, glipizide, glyburide, insulin, metformin, nateglinide, pioglitazone, repaglinide, rosiglitazone, and tolbutamide. A chart validation study showed excellent ascertainment of diabetes status using these methods (correct classification 88.8%; 95% confidence interval [CI]: 85.791.3 with weighted kappa=0.89; 95% CI: 0.85‐0.92).[11, 12] Patients without diagnosed diabetes were classified according to their peak serum glucose value during the index hospitalization: <108 mg/dL (<6.0 mmol/L), 108 to 140 mg/dL (6.07.8 mmol/L), 140 to 200 mg/dL (7.811.1 mmol/L), >200 mg/dL (>11.1 mmol/L); hospitalizations in which glucose levels were not obtained were classified as unknown. These peak serum glucose categories are based on the World Health Organization's definition of diabetes and poor glucose tolerance.[12]
Outcomes
The primary outcome was all‐cause postdischarge mortality determined by linking the index admission to the RPDB. Secondary outcomes were CV complications, including: AMI (determined by linking to the OMID); hospitalization for CHF (determined by linking to the DAD for primary diagnosis of 425, 428, 514, 518.4 or I50, I42.0, I42.6, I42.7, I42.8, I42.9, I43, J81), CVD (determined by linking to the DAD for primary diagnosis of 430, 431, 432, 434, 436 or I60, I61, I62, I63, I64, G46), PVD (determined by primary diagnosis of 96.11, 96.12, 96.13, 96.14, 96.15 [excluded if in conjunction with 170, 171, 213, 730, 740759, 800900, 901904, 940950], 50.18, 51.25, 51.29 [excluded if in conjunction with 414.1, 441, 44] or 1VC93, 1VG93, 1VQ93, 1WA93, 1WE93, 1WJ93, 1WL93, 1WM93 [excluded if in conjunction with C40, C41, C46.1, C47, C49, D160, M46.2, M86, M87, M89.6, M90.0‐M90.5, Q00, Q38‐Q40, S02.0, S09.0, S04.0, S15, S25, T26), and 1KG50, 1KG57, 1KG76, 1KG35HAC1, 1KG35HHC1 [excluded if in conjunction with I60, I67.1, I71, I72, 177.0, 179.0]), and ESRD (determined by 403.9, 404.9,584, 585, 586, 788.5 or I12, I13, N17, N18, N19, R34).
Analysis
We identified all encounters of cohort patients in any Ontario acute‐care hospital within 5 years following the index discharge. Patients not covered by provincial health insurance (OHIP) were excluded.
We first measured crude mortality and morbidity rates by patient category (diagnosed diabetes and glucose levels). Next, we compared the unadjusted outcomes and baseline characteristics (age, sex, previous inpatient and emergency admissions, and disease at admission) between groups using a [2] test for categorical variables and analysis of variance for continuous variables.
Due to the violation of proportional hazards, we used the Weibull accelerated failure time model to calculate the hazard of death associated with diabetes status or serum glucose level. Consistency of the probability plots confirmed appropriateness of using the Weibull function. Competing risk is defined as a type of failure that prevents the observation of the event of interest or fundamentally alters the probability of its occurrence.[13, 14] In the comorbidity analyses, death is a competing risk for all other outcomes. We calculated the multivariate competing risk hazard for each outcome of interest except death. Each model was adjusted for potential confounders: baseline risk of in‐hospital mortality, common comorbidities, most responsible hospital service, and the number of previous inpatient admissions and emergency department visits to TOH in the previous 6 months. The probability of dying during the admission was calculated using the Escobar model, which predicts the in‐hospital probability of dying using data available at the time of admission to the hospital.[15] The Escobar model has been validated in the study population.[16] The baseline probability of dying was based on age, sex, acuity of admission, primary condition, Charlson comorbidity score,[17] and the laboratory‐based acute physiology score.[15] The Charlson comorbidity score was calculated using weights from Schneeweiss et al.[17] Kaplan‐Meier survival curves were created for both adjusted and unadjusted models. Death was used as the main censoring variable when analyzing nonfatal outcomes at 1‐ and 5‐year follow‐up.
Adjusted models were constructed using a stepwise selection technique and compared with Akaike and Bayesian information criteria values. For all tests, significance was defined as a P value of 0.05 or less.
We recognize that the cohort may contain more than 1 index hospitalization per patient. However, repeated analyses using only the first or last encounter per patient produced nearly identical hazard ratios (HRs) and CIs.
RESULTS
Between January 1, 1996 and March 31, 2008, 194,641 nonpsychiatric and nonobstetric adults were admitted to TOH. Seventeen patients were excluded because they were ineligible for healthcare coverage and had no encounter with the Ontario healthcare system following discharge from hospital, and 11,175 of the admissions ended in death. The final cohort consisted of 114,764 unique individuals representing 183,449 encounters.
Patients had a mean age of 59.5 years (standard deviation: 18.0) and 48.9% were male. The baseline risk of dying during hospitalization was 4.8%.
Table 1 describes patients by diabetes and peak serum glucose status. Patients with diagnosed diabetes were more likely to be older and male. Patients with elevated peak serum glucose (>200 mg/dL; >11.1 mmol/L) were younger than the diagnosed diabetes group and had a higher baseline probability of in‐hospital death (9.4%, 95% CI: 9.09.7). Patients in these 2 groups had more inpatient admissions within the previous 6 months compared to the groups with other peak serum glucose values.
| Serum Glucose Level, mg/dL | ||||||
|---|---|---|---|---|---|---|
| Diagnosed Diabetes, n=32,774, 17.9% | >200, n=5,082, 2.8% | 140200, n=25,857, 14.1% | 108140, n=38,741, 21.1% | <108, n=27,603, 15.0% | Unknown, n=53,392, 29.1% | |
| ||||||
| Age, y, mean (SD) | 65.8 (14.1) | 64.3 (17.0)a | 63.9 (17.3)a | 60.9 (18.6)a | 54.3 (19.7)a | 54.8 (16.9)a |
| Risk‐adjusted mortality at admission, mean (SD) | 0.08 (0.12) | 0.09 (0.12)a | 0.07 (0.10)a | 0.05 (0.09)a | 0.04 (0.07)a | 0.01 (0.04)a |
| Sex, male, no. (%) | 18,200 (55.5) | 2,610 (51.4)a | 13,477 (52.1)a | 19,495 (50.3)a | 12,907 (46.8)a | 22,951 (43.0)a |
| No. of previous inpatient admissions, 6 months (%) | ||||||
| 0 | 22,780 (69.5) | 3,576 (70.4) | 19,118 (73.9)a | 28,827 (74.4)a | 20,354 (73.7)a | 43,317 (81.1)a |
| 1 | 6,470 (19.7) | 962 (18.9) | 4,484 (17.3)a | 6,526 (16.9)a | 4,744 (17.2)a | 7,360 (13.8)a |
| 2+ | 3,524 (10.8) | 544 (10.7) | 2,255 (8.7)a | 3,388 (9.1)a | 2,505 (9.1)a | 2,715 (5.1)a |
| No. of previous emergency admissions (6 months) (%) | ||||||
| 0 | 15,518 (47.4) | 2,638 (51.9)a | 12,681 (49.0)a | 16,584 (42.8)a | 13,039 (47.2) | 43,112 (80.8)a |
| 1 | 9,665 (29.5) | 1,490 (29.3)a | 8,339 (32.3)a | 13,829 (35.7)a | 8,709 (31.6) | 6,533 (12.2)a |
| 2+ | 7,591 (23.2) | 954 (18.8)a | 4,837 (18.7)a | 8,328 (21.5)a | 5,855 (21.2) | 3,747 (7.0)a |
| Emergency admission at index hospitalization (%) | 25,420 (77.6) | 4,178 (82.2)a | 20,284 (78.5)a | 33,282 (85.9)a | 23,598 (85.5)a | 15,039 (28.2)a |
| Length of stay, d (mean/SD) | 12.4 (22.3) | 15.8 (30.0)a | 11.9 (17.1)a | 8.5 (12.2)a | 6.3 (9.5)a | 3.4 (4.9)a |
| Disease at index hospitalization (%) | ||||||
| PVD | 2,783 (8.5) | 257 (5.1)a | 1,387 (5.4)a | 1,372 (3.5)a | 908 (3.3)a | 965 (1.8)a |
| Pneumonia | 3,308 (10.1) | 658 (13.0)a | 2,577 (10.0) | 2,809 (7.3)a | 1,220 (4.4)a | 399 (0.8)a |
| UTI | 3,549 (10.8) | 665 (13.1)a | 2,660 (10.3)a | 3,336 (8.6)a | 1,559 (5.7)a | 929 (1.7)a |
| IHD | 8,957 (27.3) | 1,086 (21.4)a | 4,714 (18.2)a | 5,306 (13.7)a | 3,100 (11.2)a | 2,842 (5.3)a |
| Hypertension | 10,864 (33.2) | 1,115 (21.9)a | 5,155 (19.9)a | 5,880 (15.2)a | 3,045 (11.0)a | 3,211 (6.0)a |
| Arrhythmia | 5,010 (15.3) | 823 (16.2) | 3,768 (14.6)a | 3,718 (9.6)a | 2,046 (7.4)a | 1,172 (2.2)a |
| CHF | 570 (17.5) | 763 (15.0)a | 2,761 (10.7)a | 2,449 (6.3)a | 1,121 (4.1)a | 386 (0.7)a |
| Diagnoses of diabetes in the next year (%) | 126 (2.5) | 368 (1.4) | 370 (1.0) | 215 (0.8) | 540 (1.0) | |
| Diagnoses of diabetes in the next 5 years (%) | 310 (6.1) | 981 (3.8) | 916 (2.4) | 434 (1.7) | 1,317 (2.5) | |
| First 3 most common primary discharge codes | AHD I251 (5.7%), HF I50 (3.1%), NSTEMI I214 (1.6%) | AHD I251 (2.7%), COPD J441 (2.1%), HF I50 (2.0%) | AHD I251 (4.0%), Pneumonia J189 (1.6%), HF I50 (1.5%) | AHD I251 (1.6%), Pneumonia J189 (1.5%), CA D700 (1.3%) | AHD I251 (1.8%), AA K359 (1.7%), UA I200 (1.2%) | OA M171 (2.3%), AHD I251 (2.2%), OA M170 (1.7%) |
Of the 5082 patients classified with a peak serum glucose measurement >200 mg/dL (11.1 mmol/L), 15% had 2 and 8% had more than 2 serum glucose measurements that exceeded this threshold. For the remaining patients (with 1 peak serum glucose measurement >200 mg/dL), 52% had additional serum glucose measurements over 140 mg/dL (7.8 mmol/L).
Table 2 presents crude 1‐ and 5‐year mortality and morbidity rates by patient group. The mortality rate is the percentage of patients who died within 1 year and 5 years of their index admission, with or without developing a CV complication. Morbidity rate describes the percentage who developed the complication among patients who survived after discharge or developed the complication prior to death within a 1‐year and 5‐year period. During the 1‐year follow‐up period, the crude mortality rate among patients with elevated peak serum glucose was higher than all other groups (25.4% vs 20.6% for diagnosed diabetes and 7.4% to 22.5% for other peak serum glucose levels; all P<0.0001). For the 5‐year follow‐up, the gap between patients with elevated peak serum glucose and those with diagnosed diabetes lessened but remained significant (45.1% vs 41.7%; P<0.0001). In the 1‐year follow‐up, patients with diagnosed diabetes had significantly higher morbidity rates than all other groups except for AMI. The difference in the rate of AMI for diagnosed diabetes and patients with elevated glucose was not statistically significant.
| Diagnosed Diabetes, n=32,774 | Serum Glucose Level (mg/dL) | |||||
|---|---|---|---|---|---|---|
| >200, n=5,082 | 140200, n=25,857 | 108140, n=38,741 | <108, n=27,603 | Unknown, n=53,392 | ||
| ||||||
| All‐cause death | ||||||
| 1 year | 6,762 (20.6) | 1,293 (25.4)a | 5,309 (20.5) | 7,212 (18.6)a | 4,178 (15)a | 3,969 (7.4)a |
| 5 years | 13,659 (41.7) | 2,292 (45.1)a | 9,871 (38.2)a | 13,256 (34.2)a | 7,606 (27.6)a | 98,614 (16.1)a |
| AMI | ||||||
| 1 year | 728 (2.8) | 104 (2.7) | 326 (1.6)a | 386 (1.2)a | 172 (0.7)a | 218 (0.4)a |
| 5 years | 1,687 (8.4) | 182 (6.3)a | 687 (4.2)a | 837 (3.2)a | 436 (2.2)a | 633 (1.4)a |
| CVD | ||||||
| 1 year | 582 (2.2) | 71 (1.9) | 306 (1.5)a | 403 (1.3)a | 251 (1.1)a | 195 (0.4)a |
| 5 years | 1,153 (5.8) | 143 (5.0) | 623 (3.8)a | 872 (3.4)a | 470 (2.3)a | 534 (1.2)a |
| CHF | ||||||
| 1 year | 2,260 (8.4) | 245 (6.3)a | 870 (4.2)a | 1,023 (3.2)a | 516 (2.2)a | 362 (0.7)a |
| 5 years | 3,830 (17.7) | 395 (12.9)a | 1,529 (9.0)a | 1,802 (6.8)a | 960 (4.7)a | 884 (2.0)a |
| PVD | ||||||
| 1 year | 795 (3.0) | 24 (0.6)a | 114 (0.6)a | 154 (0.5)a | 97 (0.4)a | 141 (0.3)a |
| 5 years | 1,547 (7.8) | 50 (1.8)a | 220 (1.4)a | 275 (1.1)a | 192 (1.0)a | 295 (0.7)a |
| ESRD | ||||||
| 1 year | 953 (3.6) | 104 (2.7)a | 403 (1.9)a | 457 (1.4)a | 311 (1.3)a | 329 (0.7)a |
| 5 years | 1,938 (9.5) | 183 (6.3)a | 807 (4.9)a | 995 (3.8)a | 611 (3.0)a | 771 (1.7)a |
The 1‐year adjusted hazard ratios for mortality and CV complications are presented in Figure 1. After adjustment for baseline demographics and clinical and hospital factors, having a peak serum glucose level above 200 mg/dL (11.1 mmol/L) was an independent predictor of death. The mortality risk for this group in the year following discharge was 31% higher than patients with diagnosed diabetes (adjusted HR: 1.31, 95% CI: 1.20‐1.43). There was no mortality risk difference between the group with diagnosed diabetes and the lower peak serum glucose levels (adjusted HR: 1.05, 95% CI: 0.99‐1.11), 108160 mg/dL (6.07.8 mmol/L) (adjusted HR: 1.02, 95% CI: 0.971.07); and <108 mg/dL (<6.0 mmol/L) (adjusted HR: 0.97, 95% CI: 0.921.03). Adjusted HRs, with 95% CIs and P values for 5‐year follow‐up are presented in Figure 2.


Adjusted hazard ratios for morbidity showed a different pattern. Patients with diagnosed diabetes had a higher risk of developing complications in the year following discharge from the hospital (Figure 1). After adjusting for potential confounders, we found that patients with diagnosed diabetes had the same risk of AMI and CVD as patients with peak serum glucose levels above 200 mg/dL (11.1 mmol/L) (AMI, adjusted HR: 0.96; 95% CI: 0.78‐1.18; CVD, adjusted HR: 0.79; 95% CI: 0.61‐1.00) but a 36% to 57% higher AMI risk and 29% to 34% higher CVD risk than other peak serum glucose level groups. Compared to all peak serum glucose groups, patients with diagnosed diabetes had a significantly higher risk of developing CHF, PVD, and ESRD (Figure 1). Similarly, the 5‐year risk of AMI, CVD, CHF, PVD, and ESRD was higher for patients with diagnosed diabetes compared to all peak serum glucose groups (Figure 2).
CONCLUSION/DISCUSSION
The study found that in‐hospital hyperglycemia was a strong predictor of mortality at 1‐ and 5‐years follow‐up, even after adjustment using well‐established and discriminating comorbidity measures. Extreme in‐hospital hyperglycemia was a stronger predictor of mortality than diagnosed diabetes.
Previous studies have shown that diabetes and stress hyperglycemia among hospitalized patients are important markers for poor clinical outcomes and in‐hospital mortality.[1, 2, 4] This study indicates that hospitalized patients with extreme hyperglycemia (peak serum glucose >200 mg/dL) were at a high risk of death for at least 5 years following discharge.
These findings, based on a large general sample of hospitalized patients, indicate that the extreme elevations in peak serum glucose convey a risk for all hospitalized patients, not only those with critical illness.[3, 18] Hyperglycemia appears to be an independent indicator of mortality risk and should be evaluated as a potential component within risk prediction tools. Further study is required to determine mechanisms for this risk association to identify what therapies, if any, might be used to minimize this risk.
The diagnosed diabetes group, which likely included some patients who also had extreme in‐hospital hyperglycemia, had a lower 1‐year risk of death than patients with hyperglycemia who did not have diabetes diagnosis. This may be an indication of the protective effect of blood glucose control, because patients with diabetes are more likely to receive therapy for hyperglycemia during and after hospitalization.
Classification of patients by several serum glucose levels (as opposed to a dichotomous classification, where hyperglycemia is either present or absent), showed that hyperglycemia constitutes a graded risk[5] for almost all outcomes examined, particularly mortality, AMI, and CVD.
Previous studies indicate that diabetes is observed in only 23% to 35% of hospitalized patients with hyperglycemia.[18, 19] We would expect higher risk for CV complications for patients with elevated glucose if the proportion of these patients who had undiagnosed diabetes was higher than the proportion estimated in the literature. However, we observed lower risk of CV complications (especially PVD and ESRD) for the elevated glucose group in the 1 and 5 years following discharge. In‐hospital hyperglycemia is not equivalent to undiagnosed diabetes.
There are several potential limitations in this study. The first is our method for ascertaining CV complications. Diverse disease definitions are used in medical literature, and similar studies using different definitions may yield different results, though we would not expect to find a wide range of variation. Second, our study did not include information about severity of diabetes and the persistence of elevated glucose; if available, this knowledge may provide better insight into patient experiences, especially in long‐term follow‐up. Third, results are also limited by the absence of data on cause of death, a potentially helpful means of identifying posthospitalization difficulties experienced by patients with hyperglycemia. Fourth, this study mainly compares experiences of patients with elevated peak serum glucose level to diabetes patients; it would be worthwhile to explore the impact of lower gradations of glucose levels.
We would like to emphasize that we did not confirm diabetes diagnosis following discharge for patients with hyperglycemia. However, we did not observe a high rate of complications at 5‐year follow‐up, particularly for ESRD. This may be because most patients with in‐hospital elevated glucose had early diabetes or transient hyperglycemia and therefore lower risk of long‐term diabetes‐specific consultations.
Hyperglycemia is an important independent indicator, carrying a greater risk for 1‐ and 5‐year mortality than diagnosed diabetes. However, it is unclear whether hospitalized patients with elevated peak serum glucose have early diabetes or their hyperglycemia reflects hospital stress or another comorbidity concept.
Acknowledgements
The authors are grateful to Amy Zierler and Allison Whalen O'Connor for their editorial assistance. This study was supported by the Institute for Clinical Evaluative Sciences (ICES), which is funded by an annual grant from the Ontario Ministry of Health and Long‐Term Care (MOHLTC). The opinions, results and conclusions reported in this paper are those of the authors and are independent from the funding sources. No endorsement by ICES or the Ontario MOHLTC is intended or should be inferred.
Disclosure: Nothing to report.
Hyperglycemia in hospitalized patients is frequently observed and is recognized as an important threat to the health of patients with varying levels of illness, independent of diabetes status.[1, 2, 3, 4] Previous studies have found that in‐hospital hyperglycemia is associated with higher short‐term mortality rates,[5, 6, 7] longer lengths of stay, and higher rates of admission to intensive care units.[4]
In‐hospital hyperglycemia may be the result of diabetes mellitus or stress associated with hospitalization. The mechanism of stress hyperglycemia differs from diabetic hyperglycemia and can occur independently of diabetes status.[8] Stress hyperglycemia is characterized by rapid onset of insulin resistance, which normally takes months or years in diabetes mellitus. It develops in association with or because of other stressor such as infection or inflammatory processes.[9]
To our knowledge, no long‐term follow‐up study on hospitalized patients with elevated glucose levels but without a diabetes diagnosis has ever been conducted. In this study, we measured the 1‐ and 5‐year risk of mortality and diabetes‐related diseases for hospitalized patients with a diabetes diagnosis compared with patients grouped according to their peak in‐hospital serum glucose level. Our primary comparison was between patients with diagnosed diabetes and those with peak serum glucose >200 mg/dL (11.1 mmol/L), but we also examined 4 other categories of peak serum glucose: 140 to 200 mg/dL (7.811.1 mmol/L), 108 to 140 mg/dL (6.07.8 mmol/L), and <108 mg/dL (<6.0 mmol/L).
METHODS
Study Base
The study included all adult patients (excluding patients admitted to psychiatry and obstetrics) admitted to The Ottawa Hospital (TOH) between January 1, 1996 and March 31, 2008 and discharged alive. Included patients were 18 years or older and had complete medical record abstracts. TOH is the primary hospital in Ottawa, Ontario, Canada, and the main tertiary hospital in the Champlain Local Health Integration Network, the public healthcare authority for the Ottawa region. This study was approved by The Ottawa Hospital Research Ethics Board.
Data Sources
The Ottawa Hospital Data Warehouse (OHDW) is a repository for data from the hospital's patient information systems. These systems include patient registration information, discharge abstract, and laboratory, pharmacy, and radiology results. OHDW was used to determine each patient's age, gender, diagnoses, pharmacy orders, laboratory test results, in‐hospital comorbidities, most responsible hospital service, and admission urgency.
This dataset was linked to 3 population‐based administrative datasets and 1 derived cohort. Ontario's Registered Persons Database (RPDB) is a population‐based registry containing date of death (if applicable) as well as eligibility status for the provincial universal health insurance program, the Ontario Health Insurance Plan (OHIP).[10] The OHIP database records billing claims submitted by approximately 95% of Ontario physicians. Each claim contains a fee code describing the type of service provided and a location denoting where the service had taken place. The Canadian Institute for Health Information Discharge Abstract Database (DAD) records clinical, demographic, and administrative data for all hospital admissions and same‐day surgeries for all Ontario acute care hospitals since April 1, 1988. The Ontario Myocardial Infarction Database (OMID) contains records of all patients with a most responsible diagnosis of acute myocardial infarction (AMI) (International Classification of Diseases, 9th Revision [ICD‐9] code 410 or International Classification of Diseases, 10th Revision [ICD‐10] code I21) identified from the DAD. Details on the creation of the OMID are provided in an earlier study.[10]
Variable Definitions
We identified the index admission of the TOH cohort in the DAD using a unique encrypted health insurance number, admission and discharge dates, and the institution number. To avoid double counting, patients with the same encrypted health insurance number who were discharged from an institution and admitted to another within 2 days were classified as transfers and counted as 1 hospitalization.
Diabetes and cardiovascular (CV) complications (acute myocardial infarction [AMI], congestive heart failure [CHF], cardiovascular disease [CVD], peripheral vascular disease [PVD], and end‐stage renal disease [ESRD]) were identified in the discharge abstract as the most responsible diagnosis for the admission as well as postadmission comorbidities. The discharge abstract records diagnostic codes according to ICD‐9 (April 1, 1988March 31, 2002) or ICD‐10 (April 1, 2002March 1, 2009).
Each hospitalization was classified into 1 of 6 mutually exclusive diabetes status categories based on diagnostic codes, serum glucose test results, and pharmacy records. The diagnosed diabetes group included hospitalizations with any diagnostic code of diabetes in the discharge abstract or any order for a diabetes medication during hospitalization. Eligible medications included acarbose, acetohexamide, chlorpropamide, glibenclamide, gliclazide, glimepiride, glipizide, glyburide, insulin, metformin, nateglinide, pioglitazone, repaglinide, rosiglitazone, and tolbutamide. A chart validation study showed excellent ascertainment of diabetes status using these methods (correct classification 88.8%; 95% confidence interval [CI]: 85.791.3 with weighted kappa=0.89; 95% CI: 0.85‐0.92).[11, 12] Patients without diagnosed diabetes were classified according to their peak serum glucose value during the index hospitalization: <108 mg/dL (<6.0 mmol/L), 108 to 140 mg/dL (6.07.8 mmol/L), 140 to 200 mg/dL (7.811.1 mmol/L), >200 mg/dL (>11.1 mmol/L); hospitalizations in which glucose levels were not obtained were classified as unknown. These peak serum glucose categories are based on the World Health Organization's definition of diabetes and poor glucose tolerance.[12]
Outcomes
The primary outcome was all‐cause postdischarge mortality determined by linking the index admission to the RPDB. Secondary outcomes were CV complications, including: AMI (determined by linking to the OMID); hospitalization for CHF (determined by linking to the DAD for primary diagnosis of 425, 428, 514, 518.4 or I50, I42.0, I42.6, I42.7, I42.8, I42.9, I43, J81), CVD (determined by linking to the DAD for primary diagnosis of 430, 431, 432, 434, 436 or I60, I61, I62, I63, I64, G46), PVD (determined by primary diagnosis of 96.11, 96.12, 96.13, 96.14, 96.15 [excluded if in conjunction with 170, 171, 213, 730, 740759, 800900, 901904, 940950], 50.18, 51.25, 51.29 [excluded if in conjunction with 414.1, 441, 44] or 1VC93, 1VG93, 1VQ93, 1WA93, 1WE93, 1WJ93, 1WL93, 1WM93 [excluded if in conjunction with C40, C41, C46.1, C47, C49, D160, M46.2, M86, M87, M89.6, M90.0‐M90.5, Q00, Q38‐Q40, S02.0, S09.0, S04.0, S15, S25, T26), and 1KG50, 1KG57, 1KG76, 1KG35HAC1, 1KG35HHC1 [excluded if in conjunction with I60, I67.1, I71, I72, 177.0, 179.0]), and ESRD (determined by 403.9, 404.9,584, 585, 586, 788.5 or I12, I13, N17, N18, N19, R34).
Analysis
We identified all encounters of cohort patients in any Ontario acute‐care hospital within 5 years following the index discharge. Patients not covered by provincial health insurance (OHIP) were excluded.
We first measured crude mortality and morbidity rates by patient category (diagnosed diabetes and glucose levels). Next, we compared the unadjusted outcomes and baseline characteristics (age, sex, previous inpatient and emergency admissions, and disease at admission) between groups using a [2] test for categorical variables and analysis of variance for continuous variables.
Due to the violation of proportional hazards, we used the Weibull accelerated failure time model to calculate the hazard of death associated with diabetes status or serum glucose level. Consistency of the probability plots confirmed appropriateness of using the Weibull function. Competing risk is defined as a type of failure that prevents the observation of the event of interest or fundamentally alters the probability of its occurrence.[13, 14] In the comorbidity analyses, death is a competing risk for all other outcomes. We calculated the multivariate competing risk hazard for each outcome of interest except death. Each model was adjusted for potential confounders: baseline risk of in‐hospital mortality, common comorbidities, most responsible hospital service, and the number of previous inpatient admissions and emergency department visits to TOH in the previous 6 months. The probability of dying during the admission was calculated using the Escobar model, which predicts the in‐hospital probability of dying using data available at the time of admission to the hospital.[15] The Escobar model has been validated in the study population.[16] The baseline probability of dying was based on age, sex, acuity of admission, primary condition, Charlson comorbidity score,[17] and the laboratory‐based acute physiology score.[15] The Charlson comorbidity score was calculated using weights from Schneeweiss et al.[17] Kaplan‐Meier survival curves were created for both adjusted and unadjusted models. Death was used as the main censoring variable when analyzing nonfatal outcomes at 1‐ and 5‐year follow‐up.
Adjusted models were constructed using a stepwise selection technique and compared with Akaike and Bayesian information criteria values. For all tests, significance was defined as a P value of 0.05 or less.
We recognize that the cohort may contain more than 1 index hospitalization per patient. However, repeated analyses using only the first or last encounter per patient produced nearly identical hazard ratios (HRs) and CIs.
RESULTS
Between January 1, 1996 and March 31, 2008, 194,641 nonpsychiatric and nonobstetric adults were admitted to TOH. Seventeen patients were excluded because they were ineligible for healthcare coverage and had no encounter with the Ontario healthcare system following discharge from hospital, and 11,175 of the admissions ended in death. The final cohort consisted of 114,764 unique individuals representing 183,449 encounters.
Patients had a mean age of 59.5 years (standard deviation: 18.0) and 48.9% were male. The baseline risk of dying during hospitalization was 4.8%.
Table 1 describes patients by diabetes and peak serum glucose status. Patients with diagnosed diabetes were more likely to be older and male. Patients with elevated peak serum glucose (>200 mg/dL; >11.1 mmol/L) were younger than the diagnosed diabetes group and had a higher baseline probability of in‐hospital death (9.4%, 95% CI: 9.09.7). Patients in these 2 groups had more inpatient admissions within the previous 6 months compared to the groups with other peak serum glucose values.
| Serum Glucose Level, mg/dL | ||||||
|---|---|---|---|---|---|---|
| Diagnosed Diabetes, n=32,774, 17.9% | >200, n=5,082, 2.8% | 140200, n=25,857, 14.1% | 108140, n=38,741, 21.1% | <108, n=27,603, 15.0% | Unknown, n=53,392, 29.1% | |
| ||||||
| Age, y, mean (SD) | 65.8 (14.1) | 64.3 (17.0)a | 63.9 (17.3)a | 60.9 (18.6)a | 54.3 (19.7)a | 54.8 (16.9)a |
| Risk‐adjusted mortality at admission, mean (SD) | 0.08 (0.12) | 0.09 (0.12)a | 0.07 (0.10)a | 0.05 (0.09)a | 0.04 (0.07)a | 0.01 (0.04)a |
| Sex, male, no. (%) | 18,200 (55.5) | 2,610 (51.4)a | 13,477 (52.1)a | 19,495 (50.3)a | 12,907 (46.8)a | 22,951 (43.0)a |
| No. of previous inpatient admissions, 6 months (%) | ||||||
| 0 | 22,780 (69.5) | 3,576 (70.4) | 19,118 (73.9)a | 28,827 (74.4)a | 20,354 (73.7)a | 43,317 (81.1)a |
| 1 | 6,470 (19.7) | 962 (18.9) | 4,484 (17.3)a | 6,526 (16.9)a | 4,744 (17.2)a | 7,360 (13.8)a |
| 2+ | 3,524 (10.8) | 544 (10.7) | 2,255 (8.7)a | 3,388 (9.1)a | 2,505 (9.1)a | 2,715 (5.1)a |
| No. of previous emergency admissions (6 months) (%) | ||||||
| 0 | 15,518 (47.4) | 2,638 (51.9)a | 12,681 (49.0)a | 16,584 (42.8)a | 13,039 (47.2) | 43,112 (80.8)a |
| 1 | 9,665 (29.5) | 1,490 (29.3)a | 8,339 (32.3)a | 13,829 (35.7)a | 8,709 (31.6) | 6,533 (12.2)a |
| 2+ | 7,591 (23.2) | 954 (18.8)a | 4,837 (18.7)a | 8,328 (21.5)a | 5,855 (21.2) | 3,747 (7.0)a |
| Emergency admission at index hospitalization (%) | 25,420 (77.6) | 4,178 (82.2)a | 20,284 (78.5)a | 33,282 (85.9)a | 23,598 (85.5)a | 15,039 (28.2)a |
| Length of stay, d (mean/SD) | 12.4 (22.3) | 15.8 (30.0)a | 11.9 (17.1)a | 8.5 (12.2)a | 6.3 (9.5)a | 3.4 (4.9)a |
| Disease at index hospitalization (%) | ||||||
| PVD | 2,783 (8.5) | 257 (5.1)a | 1,387 (5.4)a | 1,372 (3.5)a | 908 (3.3)a | 965 (1.8)a |
| Pneumonia | 3,308 (10.1) | 658 (13.0)a | 2,577 (10.0) | 2,809 (7.3)a | 1,220 (4.4)a | 399 (0.8)a |
| UTI | 3,549 (10.8) | 665 (13.1)a | 2,660 (10.3)a | 3,336 (8.6)a | 1,559 (5.7)a | 929 (1.7)a |
| IHD | 8,957 (27.3) | 1,086 (21.4)a | 4,714 (18.2)a | 5,306 (13.7)a | 3,100 (11.2)a | 2,842 (5.3)a |
| Hypertension | 10,864 (33.2) | 1,115 (21.9)a | 5,155 (19.9)a | 5,880 (15.2)a | 3,045 (11.0)a | 3,211 (6.0)a |
| Arrhythmia | 5,010 (15.3) | 823 (16.2) | 3,768 (14.6)a | 3,718 (9.6)a | 2,046 (7.4)a | 1,172 (2.2)a |
| CHF | 570 (17.5) | 763 (15.0)a | 2,761 (10.7)a | 2,449 (6.3)a | 1,121 (4.1)a | 386 (0.7)a |
| Diagnoses of diabetes in the next year (%) | 126 (2.5) | 368 (1.4) | 370 (1.0) | 215 (0.8) | 540 (1.0) | |
| Diagnoses of diabetes in the next 5 years (%) | 310 (6.1) | 981 (3.8) | 916 (2.4) | 434 (1.7) | 1,317 (2.5) | |
| First 3 most common primary discharge codes | AHD I251 (5.7%), HF I50 (3.1%), NSTEMI I214 (1.6%) | AHD I251 (2.7%), COPD J441 (2.1%), HF I50 (2.0%) | AHD I251 (4.0%), Pneumonia J189 (1.6%), HF I50 (1.5%) | AHD I251 (1.6%), Pneumonia J189 (1.5%), CA D700 (1.3%) | AHD I251 (1.8%), AA K359 (1.7%), UA I200 (1.2%) | OA M171 (2.3%), AHD I251 (2.2%), OA M170 (1.7%) |
Of the 5082 patients classified with a peak serum glucose measurement >200 mg/dL (11.1 mmol/L), 15% had 2 and 8% had more than 2 serum glucose measurements that exceeded this threshold. For the remaining patients (with 1 peak serum glucose measurement >200 mg/dL), 52% had additional serum glucose measurements over 140 mg/dL (7.8 mmol/L).
Table 2 presents crude 1‐ and 5‐year mortality and morbidity rates by patient group. The mortality rate is the percentage of patients who died within 1 year and 5 years of their index admission, with or without developing a CV complication. Morbidity rate describes the percentage who developed the complication among patients who survived after discharge or developed the complication prior to death within a 1‐year and 5‐year period. During the 1‐year follow‐up period, the crude mortality rate among patients with elevated peak serum glucose was higher than all other groups (25.4% vs 20.6% for diagnosed diabetes and 7.4% to 22.5% for other peak serum glucose levels; all P<0.0001). For the 5‐year follow‐up, the gap between patients with elevated peak serum glucose and those with diagnosed diabetes lessened but remained significant (45.1% vs 41.7%; P<0.0001). In the 1‐year follow‐up, patients with diagnosed diabetes had significantly higher morbidity rates than all other groups except for AMI. The difference in the rate of AMI for diagnosed diabetes and patients with elevated glucose was not statistically significant.
| Diagnosed Diabetes, n=32,774 | Serum Glucose Level (mg/dL) | |||||
|---|---|---|---|---|---|---|
| >200, n=5,082 | 140200, n=25,857 | 108140, n=38,741 | <108, n=27,603 | Unknown, n=53,392 | ||
| ||||||
| All‐cause death | ||||||
| 1 year | 6,762 (20.6) | 1,293 (25.4)a | 5,309 (20.5) | 7,212 (18.6)a | 4,178 (15)a | 3,969 (7.4)a |
| 5 years | 13,659 (41.7) | 2,292 (45.1)a | 9,871 (38.2)a | 13,256 (34.2)a | 7,606 (27.6)a | 98,614 (16.1)a |
| AMI | ||||||
| 1 year | 728 (2.8) | 104 (2.7) | 326 (1.6)a | 386 (1.2)a | 172 (0.7)a | 218 (0.4)a |
| 5 years | 1,687 (8.4) | 182 (6.3)a | 687 (4.2)a | 837 (3.2)a | 436 (2.2)a | 633 (1.4)a |
| CVD | ||||||
| 1 year | 582 (2.2) | 71 (1.9) | 306 (1.5)a | 403 (1.3)a | 251 (1.1)a | 195 (0.4)a |
| 5 years | 1,153 (5.8) | 143 (5.0) | 623 (3.8)a | 872 (3.4)a | 470 (2.3)a | 534 (1.2)a |
| CHF | ||||||
| 1 year | 2,260 (8.4) | 245 (6.3)a | 870 (4.2)a | 1,023 (3.2)a | 516 (2.2)a | 362 (0.7)a |
| 5 years | 3,830 (17.7) | 395 (12.9)a | 1,529 (9.0)a | 1,802 (6.8)a | 960 (4.7)a | 884 (2.0)a |
| PVD | ||||||
| 1 year | 795 (3.0) | 24 (0.6)a | 114 (0.6)a | 154 (0.5)a | 97 (0.4)a | 141 (0.3)a |
| 5 years | 1,547 (7.8) | 50 (1.8)a | 220 (1.4)a | 275 (1.1)a | 192 (1.0)a | 295 (0.7)a |
| ESRD | ||||||
| 1 year | 953 (3.6) | 104 (2.7)a | 403 (1.9)a | 457 (1.4)a | 311 (1.3)a | 329 (0.7)a |
| 5 years | 1,938 (9.5) | 183 (6.3)a | 807 (4.9)a | 995 (3.8)a | 611 (3.0)a | 771 (1.7)a |
The 1‐year adjusted hazard ratios for mortality and CV complications are presented in Figure 1. After adjustment for baseline demographics and clinical and hospital factors, having a peak serum glucose level above 200 mg/dL (11.1 mmol/L) was an independent predictor of death. The mortality risk for this group in the year following discharge was 31% higher than patients with diagnosed diabetes (adjusted HR: 1.31, 95% CI: 1.20‐1.43). There was no mortality risk difference between the group with diagnosed diabetes and the lower peak serum glucose levels (adjusted HR: 1.05, 95% CI: 0.99‐1.11), 108160 mg/dL (6.07.8 mmol/L) (adjusted HR: 1.02, 95% CI: 0.971.07); and <108 mg/dL (<6.0 mmol/L) (adjusted HR: 0.97, 95% CI: 0.921.03). Adjusted HRs, with 95% CIs and P values for 5‐year follow‐up are presented in Figure 2.


Adjusted hazard ratios for morbidity showed a different pattern. Patients with diagnosed diabetes had a higher risk of developing complications in the year following discharge from the hospital (Figure 1). After adjusting for potential confounders, we found that patients with diagnosed diabetes had the same risk of AMI and CVD as patients with peak serum glucose levels above 200 mg/dL (11.1 mmol/L) (AMI, adjusted HR: 0.96; 95% CI: 0.78‐1.18; CVD, adjusted HR: 0.79; 95% CI: 0.61‐1.00) but a 36% to 57% higher AMI risk and 29% to 34% higher CVD risk than other peak serum glucose level groups. Compared to all peak serum glucose groups, patients with diagnosed diabetes had a significantly higher risk of developing CHF, PVD, and ESRD (Figure 1). Similarly, the 5‐year risk of AMI, CVD, CHF, PVD, and ESRD was higher for patients with diagnosed diabetes compared to all peak serum glucose groups (Figure 2).
CONCLUSION/DISCUSSION
The study found that in‐hospital hyperglycemia was a strong predictor of mortality at 1‐ and 5‐years follow‐up, even after adjustment using well‐established and discriminating comorbidity measures. Extreme in‐hospital hyperglycemia was a stronger predictor of mortality than diagnosed diabetes.
Previous studies have shown that diabetes and stress hyperglycemia among hospitalized patients are important markers for poor clinical outcomes and in‐hospital mortality.[1, 2, 4] This study indicates that hospitalized patients with extreme hyperglycemia (peak serum glucose >200 mg/dL) were at a high risk of death for at least 5 years following discharge.
These findings, based on a large general sample of hospitalized patients, indicate that the extreme elevations in peak serum glucose convey a risk for all hospitalized patients, not only those with critical illness.[3, 18] Hyperglycemia appears to be an independent indicator of mortality risk and should be evaluated as a potential component within risk prediction tools. Further study is required to determine mechanisms for this risk association to identify what therapies, if any, might be used to minimize this risk.
The diagnosed diabetes group, which likely included some patients who also had extreme in‐hospital hyperglycemia, had a lower 1‐year risk of death than patients with hyperglycemia who did not have diabetes diagnosis. This may be an indication of the protective effect of blood glucose control, because patients with diabetes are more likely to receive therapy for hyperglycemia during and after hospitalization.
Classification of patients by several serum glucose levels (as opposed to a dichotomous classification, where hyperglycemia is either present or absent), showed that hyperglycemia constitutes a graded risk[5] for almost all outcomes examined, particularly mortality, AMI, and CVD.
Previous studies indicate that diabetes is observed in only 23% to 35% of hospitalized patients with hyperglycemia.[18, 19] We would expect higher risk for CV complications for patients with elevated glucose if the proportion of these patients who had undiagnosed diabetes was higher than the proportion estimated in the literature. However, we observed lower risk of CV complications (especially PVD and ESRD) for the elevated glucose group in the 1 and 5 years following discharge. In‐hospital hyperglycemia is not equivalent to undiagnosed diabetes.
There are several potential limitations in this study. The first is our method for ascertaining CV complications. Diverse disease definitions are used in medical literature, and similar studies using different definitions may yield different results, though we would not expect to find a wide range of variation. Second, our study did not include information about severity of diabetes and the persistence of elevated glucose; if available, this knowledge may provide better insight into patient experiences, especially in long‐term follow‐up. Third, results are also limited by the absence of data on cause of death, a potentially helpful means of identifying posthospitalization difficulties experienced by patients with hyperglycemia. Fourth, this study mainly compares experiences of patients with elevated peak serum glucose level to diabetes patients; it would be worthwhile to explore the impact of lower gradations of glucose levels.
We would like to emphasize that we did not confirm diabetes diagnosis following discharge for patients with hyperglycemia. However, we did not observe a high rate of complications at 5‐year follow‐up, particularly for ESRD. This may be because most patients with in‐hospital elevated glucose had early diabetes or transient hyperglycemia and therefore lower risk of long‐term diabetes‐specific consultations.
Hyperglycemia is an important independent indicator, carrying a greater risk for 1‐ and 5‐year mortality than diagnosed diabetes. However, it is unclear whether hospitalized patients with elevated peak serum glucose have early diabetes or their hyperglycemia reflects hospital stress or another comorbidity concept.
Acknowledgements
The authors are grateful to Amy Zierler and Allison Whalen O'Connor for their editorial assistance. This study was supported by the Institute for Clinical Evaluative Sciences (ICES), which is funded by an annual grant from the Ontario Ministry of Health and Long‐Term Care (MOHLTC). The opinions, results and conclusions reported in this paper are those of the authors and are independent from the funding sources. No endorsement by ICES or the Ontario MOHLTC is intended or should be inferred.
Disclosure: Nothing to report.
- , , , et al. Management of diabetes and hyperglycemia in hospitals. Diabetes Care. 2004;27(2):553–591.
- , , , et al. American Association of Clinical Endocrinologists and American Diabetes Association consensus statement on inpatient glycemic control. Diabetes Care. 2009;32(6):1119–1131.
- The NICE‐SUGAR Study Investigators. Intensive versus conventional glucose control in critically ill patients. N Engl J Med. 2009;360(13):1283–1297.
- , , , , , . Hyperglycemia: an independent marker of in‐hospital mortality in patients with undiagnosed diabetes. J Clin Endocrinol Metab. 2002;87(3):978–982.
- , , , , . Hyperglycemia‐related mortality in critically ill patients varies with admission diagnosis. Crit Care Med. 2009;37(12):3001–3009.
- , . Hospital management of hyperglycemia. Curr Opin Endocrinol Diabetes Obes. 2011;18(2):110–118.
- , , , et al. IScore: a risk score to predict death early after hospitalization for an acute ischemic stroke. Circulation. 2011;123(7):739–749.
- , . Does Stress‐induced hyperglycemia increase the risk of perioperative infectious complications in orthopaedic trauma patients? J Orthop Trauma. 2010;24(12):752–756.
- . Metabolic mechanisms of stress hyperglycemia. J Parenter Enteral Nutr. 2006;30(2):157–163.
- , , . Temporal changes in the outcomes of acute myocardial infarction in Ontario, 1992–1996. CMAJ. 1999;161(10):1257–1261.
- , , , et al. The accuracy of using integrated electronic health care data to identify patients with undiagnosed diabetes mellitus. J Eval Clin Pract. 2012;18(3):606–611.
- American Diabetes Association. Diagnosis and classification of diabetes mellitus. Diabetes Care. 2006;29(suppl 1):s43–s48.
- . Dealing with competing risks: testing covariates and calculating sample size. Stat Med. 2002;21(22):3317–3324.
- , , , . Competing risk analysis of events 10 years after revascularization. Scand Cardiovasc J. 2010;44(5):279–288.
- , , , , , . Risk‐adjusting hospital inpatient mortality using automated inpatient, outpatient, and laboratory databases. Med Care. 2008;46(3):232–239.
- , , , . The Kaiser Permanente inpatient risk adjustment methodology was valid in an external patient population. J Clin Epidemiol. 2010;63(7):798–803.
- , , , . Improved comorbidity adjustment for predicting mortality in medicare populations. Health Serv Res. 2003;38(4):1103–1120.
- , , , et al. Glucose metabolism in patients with acute myocardial infarction and no previous diagnosis of diabetes mellitus: a prospective study. Lancet. 2002;359(9324):2140–2144.
- , , , et al. Disorders of glucose metabolism in acute stroke patients: an underrecognized problem. Diabetes Care. 2006;29(4):792–797.
- , , , et al. Management of diabetes and hyperglycemia in hospitals. Diabetes Care. 2004;27(2):553–591.
- , , , et al. American Association of Clinical Endocrinologists and American Diabetes Association consensus statement on inpatient glycemic control. Diabetes Care. 2009;32(6):1119–1131.
- The NICE‐SUGAR Study Investigators. Intensive versus conventional glucose control in critically ill patients. N Engl J Med. 2009;360(13):1283–1297.
- , , , , , . Hyperglycemia: an independent marker of in‐hospital mortality in patients with undiagnosed diabetes. J Clin Endocrinol Metab. 2002;87(3):978–982.
- , , , , . Hyperglycemia‐related mortality in critically ill patients varies with admission diagnosis. Crit Care Med. 2009;37(12):3001–3009.
- , . Hospital management of hyperglycemia. Curr Opin Endocrinol Diabetes Obes. 2011;18(2):110–118.
- , , , et al. IScore: a risk score to predict death early after hospitalization for an acute ischemic stroke. Circulation. 2011;123(7):739–749.
- , . Does Stress‐induced hyperglycemia increase the risk of perioperative infectious complications in orthopaedic trauma patients? J Orthop Trauma. 2010;24(12):752–756.
- . Metabolic mechanisms of stress hyperglycemia. J Parenter Enteral Nutr. 2006;30(2):157–163.
- , , . Temporal changes in the outcomes of acute myocardial infarction in Ontario, 1992–1996. CMAJ. 1999;161(10):1257–1261.
- , , , et al. The accuracy of using integrated electronic health care data to identify patients with undiagnosed diabetes mellitus. J Eval Clin Pract. 2012;18(3):606–611.
- American Diabetes Association. Diagnosis and classification of diabetes mellitus. Diabetes Care. 2006;29(suppl 1):s43–s48.
- . Dealing with competing risks: testing covariates and calculating sample size. Stat Med. 2002;21(22):3317–3324.
- , , , . Competing risk analysis of events 10 years after revascularization. Scand Cardiovasc J. 2010;44(5):279–288.
- , , , , , . Risk‐adjusting hospital inpatient mortality using automated inpatient, outpatient, and laboratory databases. Med Care. 2008;46(3):232–239.
- , , , . The Kaiser Permanente inpatient risk adjustment methodology was valid in an external patient population. J Clin Epidemiol. 2010;63(7):798–803.
- , , , . Improved comorbidity adjustment for predicting mortality in medicare populations. Health Serv Res. 2003;38(4):1103–1120.
- , , , et al. Glucose metabolism in patients with acute myocardial infarction and no previous diagnosis of diabetes mellitus: a prospective study. Lancet. 2002;359(9324):2140–2144.
- , , , et al. Disorders of glucose metabolism in acute stroke patients: an underrecognized problem. Diabetes Care. 2006;29(4):792–797.
© 2014 Society of Hospital Medicine
Early Death or Hospital Readmission
Socioeconomic status (SES) classifies people according to occupation, prior education, or income.[1] Socioeconomic status has been associated with several population‐health outcomes, albeit with geographically inconsistent results.[2] If lower SES is associated with higher readmission rates, then further studies could be done to determine which specific socioeconomic factors are potentially modifiable and whether the provision of additional resources could allay the increased risk associated with those factors.
Nine studies have examined the association between SES and readmissions.[3, 4, 5, 6, 7, 8, 9, 10, 11] These studies varied extensively in methodologies, SES measures, and results. However, results from 1 of these studies[11] were particularly notable given the study's significant association between lower household income and increased risk of acute readmission in a publicly funded, open‐access healthcare system. Given the implications of these results, an accurate and explicit assessment of the association between SES measures and the risk of adverse postdischarge outcomes is important.
We recently developed a model that accurately predicts the risk of 30‐day death or urgent readmission using administrative data.[12] This model did not directly control for any SES factors. In this study, we determined if a commonly used SES measurehousehold‐income quintilewas associated with the risk of early death or urgent readmission after controlling for factors known to influence this outcome.
METHODS
Study Setting and Data Sources
This population‐based study took place in Ontario, Canada, between April 1, 2003 and March 31, 2009. All hospital and physician care in Ontario is publicly funded. The study used 2 databases, the Discharge Abstract Database and the Registered Persons Database. The Discharge Abstract Database records information about all nonpsychiatric hospitalizations, including dates of hospital admission and discharge, vital status at end of hospitalization, discharge destination (ie, community, nursing home, or chronic hospital), admission urgency, primary and other diagnoses, and postal code of patient's household. The Registered Persons Database captures basic demographic data about all Ontarians, including date of birth and date of death (if applicable), postal code of residence, and average household‐income quintile of postal code, determined by linking the postal code to Statistics Canada geographical units through the Postal Code Conversion File Plus.[13] The Registered Persons Database captures all deaths regardless of the death location (ie, community vs hospital).
Study Population
This study used patients from a previous analysis that internally validated an index to predict the risk of 30‐day death or urgent readmission.[12] This analysis included a simple random sample of 250,000 adult Ontarians (age >18 years) who were discharged from the hospital to the community between April 1, 2003 and March 31, 2009. These medical and surgical hospitalizations were sampled from the Discharge Abstract Database described above. Psychiatric admissions were excluded because their hospitalizations are captured in a distinct database; obstetrical admissions were also excluded because they have a very low risk of 30‐day death or readmission. We randomly chose 1 index admission per person to ensure that the patient was the unit of analysis.
For the present study, we selected all patients from the previous analysis who were discharged from the hospital in 2006. This year was chosen because the SES indicator we used in the study (average household‐income quintile) was measured during the 2006 Canadian Census and would be most accurate for patients discharged in that year. The present study also limited patients to those with a valid postal code, because this was required to link patients to their neighborhood and their household‐income quintile.
Study Outcome
The study outcome was all‐cause death or urgent readmission within 30 days of discharge from hospital. We combined death with urgent readmission to avoid potential biases that could occur when measuring associations between risk factors and urgent readmission; in analyses having readmission as the sole outcome, the categorization of early deaths that occur prior to readmission as nonevents could minimize the importance of factors (such as severe comorbidities or patient age) that are associated with both early death and readmission.
We linked to the Registered Patients Database to determine each person's 30‐day death status. We linked to the Discharge Abstract Database to determine if patients had been urgently readmitted to any hospital within 30 days of discharge. All deaths were considered regardless of cause. All urgent (ie, nonscheduled) readmissions were included regardless of the reason for admission. Urgent status was determined by the urgency field in the Discharge Abstract Database, for which data abstractors are instructed to classify all nonscheduled admissions as urgent; these admissions frequently include those admitted after presenting to the emergency department.
Study Covariates: Readmission Risk and Neighborhood Household‐Income Quintile
In our primary analysis, we quantified the risk of 30‐day death or urgent readmission using an internally validated index, the LACE+ index: length of stay (L), acuity of the admission (A), comorbidity of the patient (measured with the Charlson Comorbidity Index score (C), and emergency‐department use (E).[12] The LACE+ index predicts the risk of 30‐day all‐cause death or urgent readmission for nonpsychiatric and nonobstetrical admissions. This index includes patient age, sex, comorbidities, and previous hospital and emergency‐department utilization; admission urgency; hospital type; total length of stay (LOS) and days in hospital awaiting placement; and hospitalization diagnostic risk.[14] The index quantified outcome risk as a score that ranged from 17 to 114. It was very discriminatory (C statistic, 77.1%) and was well calibrated (the observed and expected outcome risk was statistically distinct in only 2 of 14 risk groups that contained <2% of the population). The LACE+ quintiles were defined using score distribution from the entire 20032009 cohort.[12]
We used neighborhood income quintile as 1 measure of patient SES. Neighborhood income quintile was calculated by Statistics Canada using the Income Per Person Equivalent (IPPE) determined from the 2006 Canadian census.[13] The IPPE was calculated as total household income divided by the Single Persons Equivalent, which reflects decreased costs per person (and therefore increased available income per household occupant) in households having greater numbers of people. Within each dissemination area (each contains 400700 people), the average IPPE was calculated. Then, within each region (delineated by the Census Metropolitan Area, the Census Agglomeration, or provincial residual areas), dissemination areas were ranked by their average IPPE and then categorized into quintiles. These household‐income quintiles, therefore, are community‐specific and ensure that neighborhood household incomes are categorized based on comparisons within the same community. As such, the income thresholds for quintile categorization will vary between regions. We linked each patient's postal code to their dissemination area using the Postal Code Conversion File Plus[13] to determine their neighborhood income quintile.
Analysis
We described the patient cohort by readmission status. We categorized the expected risk of 30‐day death or urgent readmission to hospital (as determined by the LACE+ score) into quintiles. We used the 2 test and the test for trend to determine the association of these risk quintiles and SES quintiles with observed rates of 30‐day death or urgent readmission. The Cochran‐Mantel‐Haenszel test was used to determine the association of household‐income quintile and outcome risk after adjusting for LACE+ quintile.
To determine how the association between income quintile and outcome changes with increase adjustment, we constructed a series of logistic‐regression models that contained household‐income quintile and the sequential addition of components of the LACE+ score. For each model, we measured the influence of these added covariates on the association between household‐income quintile and early death or urgent readmission. We used orthogonal parameterization (which facilitates the comparison of parameter estimates in a regression model) to measure linear trends in the association of the income quintiles with outcomes.
RESULTS
The original cohort contained 250,000 people, of which 40,827 people (16.3%) were included in the present study (208,995 were excluded because patients were discharged in years other than 2006; 178 were excluded because of invalid postal codes).
Patients are described in Table 1. Patients were middle‐aged and had few documented chronic comorbidities. Of the patients, 37% had been to the emergency department and 12% had been admitted urgently. Most admissions were to large, nonteaching hospitals with a median LOS of 3 days.
| Variable | Value | No Death/Readmission, n=38,189 | Death/Readmission, n=2,638 | Overall, N=40,827 | |||
|---|---|---|---|---|---|---|---|
| |||||||
| Mean age (SD), y | 57.39 (18.3) | 67.17 (17.2) | 58.02 (18.4) | ||||
| Female sex | 20,044 | 52.5% | 1,291 | 48.9% | 21,335 | 52.3% | |
| Charlson index | 0 | 28,908 | 75.7% | 1,238 | 46.9% | 30,146 | 73.8% |
| 1 | 450 | 11.7% | 362 | 13.7% | 4,812 | 11.8% | |
| 2 | 2,668 | 7.0% | 427 | 16.2% | 3,095 | 7.6% | |
| 3+ | 2,163 | 5.7% | 611 | 23.2% | 2,774 | 6.8% | |
| ED visits in previous 6 moths | 0 | 24,599 | 64.4% | 1,210 | 45.9% | 25,809 | 63.2% |
| 12 | 11,262 | 29.5% | 1,008 | 38.2% | 12,270 | 30.1% | |
| 3+ | 2,328 | 6.1% | 420 | 15.9% | 2,748 | 6.7% | |
| Urgent hospitalizations, previous year | 0 | 33,729 | 88.3% | 1,796 | 68.1% | 35,525 | 87.0% |
| 1 | 3,425 | 9.0% | 525 | 19.9% | 3,950 | 9.7% | |
| 1+ | 1,035 | 2.7% | 317 | 12.0% | 1,352 | 3.3% | |
| Elective hospitalizations, previous year | 0 | 35,988 | 94.2% | 2,389 | 90.6% | 38,377 | 94.0% |
| 1 | 1,998 | 5.2% | 213 | 8.1% | 2,211 | 5.4% | |
| 2+ | 203 | 0.5% | 36 | 1.4% | 239 | 0.6% | |
| Hospital type | Nonteaching, large | 20,554 | 53.8% | 1,334 | 50.6% | 21,888 | 53.6% |
| Nonteaching, small | 5,239 | 13.7% | 487 | 18.5% | 5726 | 14.0% | |
| Teaching | 12,396 | 32.5% | 817 | 31.0% | 13,213 | 32.4% | |
| Urgent admit | 23,769 | 62.2% | 2,223 | 84.3% | 25,992 | 63.7% | |
| LOS rounded to nearest day, median (IQR) | 3 (26) | 5 (311) | 3 (26) | ||||
| Any hospital days on ALC | 0 | 646 | 1.7% | 127 | 4.8% | 773 | 1.9% |
| CMG score of index admission | 0 | 27,257 | 71.4% | 1,594 | 60.4% | 28,851 | 70.7% |
| 1+ | 5,218 | 13.7% | 948 | 35.9% | 6,166 | 15.1% | |
| <0 | 5,714 | 15.0% | 96 | 3.6% | 5,810 | 14.2% | |
| LACE+ score of index admission, median (IQR) | 31 (1848) | 61 (4175) | 32 (1951) | ||||
| Household‐income quintile | 1 (poorest) | 7,798 | 20.4% | 621 | 23.5% | 8,419 | 20.6% |
| 2 | 7,812 | 20.5% | 586 | 22.2% | 8,398 | 20.6% | |
| 3 | 7,557 | 19.8% | 484 | 18.3% | 8,041 | 19.7% | |
| 4 | 7,561 | 19.8% | 500 | 19.0% | 8,061 | 19.7% | |
| 5 (richest) | 7,461 | 19.5% | 447 | 16.9% | 7,908 | 19.4% | |
Death or urgent readmission within 30 days occurred in 2638 people (6.5%) (Table 1). Outcome risk increased with age; in males; as comorbidities increased; with greater numbers of emergency‐department visits, urgent admissions, and previous elective admissions; when index admissions were emergent; with longer hospital LOS and increased number of alternate level of care days; and as the diagnostic risk (measured as the Case Mix Group [CMG] score)[14] increased. Outcome risk increased as income quintile became poorer.
Household Income and Risk of 30‐Day Death or Urgent Readmission
People were evenly divided among the income quintiles (Table 2). By itself, household‐income quintile was significantly associated with the risk of early death or urgent hospital readmission (Table 2, column C, 2=27.4, P<0.0001; Mantel‐Haenszel trend 2=24.3, P<0.0001). In the poorest quintile, 7.4% of people had an outcome, compared with 5.6% in the richest quintile (2=19.8, df=1, P<0.0001).
| Risk Quintile of 30‐Day Death or Readmission (LACE+ Points Range) | ||||||
|---|---|---|---|---|---|---|
| 1 (1416) [A] | 2 (1727) | 3 (2839) | 4 (4056) | 5 (57114) [B] | Income Quintile Overall [C] | |
| ||||||
| Income quintile | ||||||
| 1 (poorest) | 18/1,485 (1.2%) | 42/1,667 (2.5%) | 65/1,635 (4.0%) | 117/1,722 (6.8%) | 379/1,910 (19.8%) | 621/8,419 (7.4%) |
| 2 | 21/1,627 (1.3%) | 39/1,665 (2.3%) | 65/1,598 (4.1%) | 130/1,808 (5.2%) | 331/1,700 (19.5%) | 586/8,398 (7.0%) |
| 3 | 18/1,761 (1.0%) | 33/1,665 (2.0%) | 63/1,568 (4.0%) | 96/1,499 (6.4%) | 274/1,548 (17.7%) | 484/8,041 (6.0%) |
| 4 | 27/1,851 (1.5%) | 42/1,698 (2.4%) | 57/1,585 (3.6%) | 110/1,548 (6.1%) | 264/1,379 (19.1%) | 500/8,061 (6.2%) |
| 5 (richest) | 20/1,864 (1.1%) | 32/1,736 (1.8%) | 60/1,468 (4.1%) | 107/1,525 (7.0%) | 228/1,315 (17.3%) | 447/7,908 (5.6%) |
| Risk quintile overall [D] | 104/8,588 (1.2%) | 188/8,431 (2.2%) | 310/7,854 (4.0%) | 560/8,102 (6.9%) | 1476/7,852 (18.8%) | 2,638/40,827 (6.5%) |
However, household income was also strongly associated with LACE+ scores (2=240, P<0.0001; Mantel‐Haenszel trend 2=209, P<0.0001). The number of people in the lowest‐risk quintile increased with income, from 1485 in the poorest quintile to 1864 in the richest quintile (Table 2, column A). In contrast, the number of high‐risk people progressively decreased with income, from 1910 in the poorest quintile to 1315 in the richest quintile (Table 2, column B).
The LACE+ quintile was very strongly associated with outcome risk, as shown in Table 2, row D (2=2703, P<0.0001; Mantel‐Haenszel trend 2=2102, P<0.0001). Within each LACE+ stratum, the risk of death or urgent readmission did not appear to consistently change with income quintile. After adjusting for LACE+ scores, income quintile was no longer associated with 30‐day death or readmission (Cochran‐Mantel‐Haenszel 2=5.9, df=4, P=0.21).
We found no nonlinear associations between household‐income quintile and 30‐day death or readmission after adjusting for the LACE+ score. In addition, the association between LACE+ quintile and outcome did not vary significantly by household‐income quintile (P value for interaction term in logistic regression model=0.5582).
The association between income quintile and 30‐day death or urgent readmission decreased when incrementally controlling for other covariates in the LACE+ model (Figure 1). By itself, all income quintiles except 2 were significantly distinct from the poorest income quintile. The addition of patient age, sex, and hospital type had little effect on the association between income and outcomes. The addition of index admission urgency shifted all point estimates toward unity (Figure 1). Associations between income and death or readmission then remained relatively stable until the addition of number of urgent admissions in the previous year (Figure 1). The subsequent addition of number of emergency visits and comorbidities resulted in none of the income quintiles being statistically distinct from the poorest quintile, as well as a nonsignificant linear trend over the quintiles.
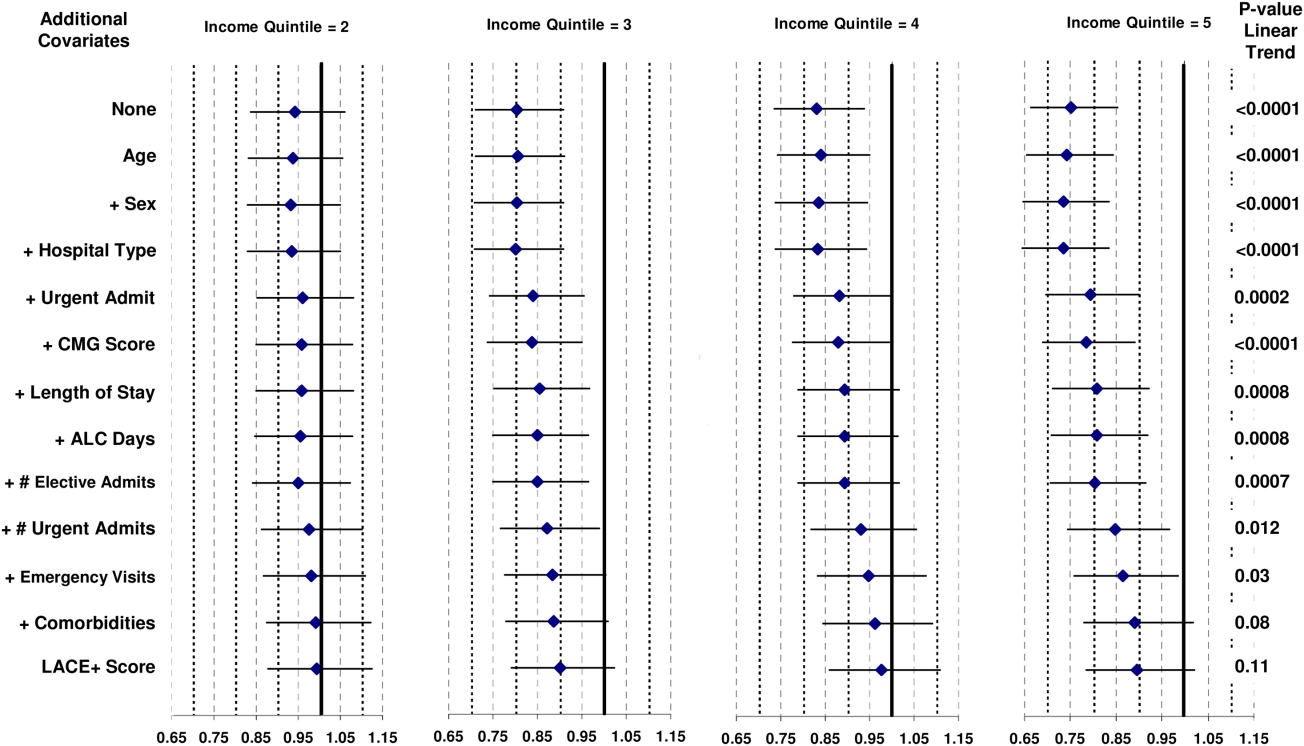
DISCUSSION
Our study shows that the risk of 30‐day death or urgent readmission was higher in people from lower‐income neighborhoods. However, this risk appears to be explained by patient‐level factors that are known to be associated with bad postdischarge outcomes. After accounting for these factors with the LACE+ index, we found no notable changes in the risk of early death or urgent readmission with SES as measured with average neighborhood household income.
Nine previous studies have measured the association between various SES measures and hospital readmission in disparate populations.[3, 4, 5, 6, 7, 8, 9, 10, 11] These studies were done in the United States,[5, 6, 8, 9, 10] the United Kingdom,[3, 7] Australia,[4] and Canada.[11] They used a range of SES indicators (from area‐level measures of household income[5] or deprivation[3] to personal education and income)[8, 9, 10] in diverse patient populations (from a random sample of all hospitalizations[3] to people with disabilities living in New York City)[15] and very different time horizons (capturing hospital readmissions that occurred from within 30 days[5] to 4 years).[10] Of these 9 studies, 5 found no independent association between their SES measure and readmission,[5, 6, 8, 9, 10] and 2 included SES in their final regression model but did not present the modelmaking it impossible to determine if SES significantly influenced outcomes.[3, 15] One study found that the risk of hospital readmission independently increased as a composite measure of area‐level social and economic indicators decreased.[4] A Canadian study[11] measured neighborhood income quintile and showed, after adjusting for patient sex, comorbidities, LOS variance, and previous admissions, that the odds of acute, nonpsychiatric readmission within 30 days of discharge were approximately 10% higher in the lowest versus the highest SES quintile. The ability of this model to adjust for important confounders when associating SES and risk of readmission is uncertain because the model fit was not reported.
Several factors could explain the difference between our study and the previous Canadian analysis showing significantly higher adjusted risk of readmission in patients from the lowest versus the highest SES quintile.[11] First, our analysis had a slightly different outcome, combining early death with urgent readmission (rather than the latter alone). We believe that this combination is important to avoid biased results when associating patient factors with readmission risk.[14] Second, our unit of analysis was the patient, whereas in the previous analysis it was the hospitalization.[11] A recent analysis by our group found that this distinction can change the results on analyses in early postdischarge outcomes.[16] In the present analysis, different results could occur if patients with multiple readmissions were disproportionately prevalent in low‐income neighborhoods. Third, our analysis was limited to Ontario rather than the entire country. Finally, and we believe most importantly, we used a validated model to control for risk of poor outcomes soon after discharge from hospital. Our analysis shows that this risk was strongly associated with neighborhood income (Table 2). This suggests that the association between SES and bad postdischarge outcomes could be explained by factors that independently increase the risk of these outcomes. Adequately controlling for these covariates would then remove variation in readmission risk by SES. We believe that these results highlight the importance of adequately controlling for potential confounders.
We believe that our results are reassuring but not definitive. We found no indication that, in Ontario, people from poorer neighborhoods are systematically more likelyafter considering factors that are known to be associated with early death or urgent readmissionto have a worse outcome early after their discharge from hospital. However, patient income and other SES measures could be associated with early death or readmission for several reasons. First, our study used average neighborhood income quintiles to quantify SES. It is possible that other SES measures (such as education or social deprivation) or patient‐level SES indicators could be significantly associated with early death or readmission.[17, 18] Second, we previously found that approximately only 25% of hospital readmissions are potentially avoidable.[19] Further study is required to determine if patient SES independently influences potentially avoidable hospital readmissions. Third, we cannot be certain how our results might generalize to health populations outside of Ontario. Specifically, SES might play a more important role in regions without universal healthcare in which community‐based healthcare resources that could decrease readmission risk, such as medications or physician follow‐up, are unavailable to those without health insurance coverage. Finally, we found notable confounding between neighborhood income quintile and factors known to be independently associated with early death or urgent readmission (Figure 1). This was especially prominent with index admission urgency, number of previous urgent admissions and emergency visits, and patient comorbidities. These factors have a much stronger association with early death or readmission than neighborhood income quintile. If low neighborhood income actually results in urgent hospital admission, emergency‐department visits, and comorbidities, then the inclusion of these covariates in the model could obscure the influence of neighborhood income on early death or readmission.
In summary, our study found that neighborhood income was not associated with early death or urgent readmission independent of known risk factors. Our analysis indicates that focusing resources on patients in lower‐income neighborhoods is unlikely to change the risk of early postdischarge adverse events. Further study is required to determine if SES is associated with adverse postdischarge outcomes in settings without publicly funded healthcare.
Acknowledgment
Disclosure: Nothing to report.
- Last JM, ed. A Dictionary of Epidemiology. 3rd ed. New York, NY: Oxford University Press; 1995.
- , , , et al. Is income inequality a determinant of population health? Part 1: A systematic review. Milbank Q. 2004;82(1):5–99.
- , , . Identifying patients at high risk of emergency hospital admissions: a logistic regression analysis. J R Soc Med. 2006;99(8):406–414.
- , , , . Using routine inpatient data to identify patients at risk of hospital readmission. BMC Health Serv Res. 2009;9:96.
- , , , , . Risk factors for 30‐day hospital readmission in patients ≥65 years of age. Proc (Bayl Univ Med Cent). 2008;21(4):363–372.
- , , , et al. An automated model to identify heart failure patients at risk for 30‐day readmission or death using electronic medical record data. Med Care. 2010;48(11):981–988.
- , . Improving the management of care for high‐cost Medicaid patients. Health Aff (Millwood). 2007;26(6):1643–1654.
- , . Factors predicting readmission of older general medicine patients. J Gen Intern Med. 1991;6(5):389–393.
- , , , et al. Hospital readmission in general medicine patients: a prediction model. J Gen Intern Med. 2010;25(3):211–219.
- , , , , , . Screening elders for risk of hospital admission. J Am Geriatr Soc. 1993;41(8):811–817.
- Canadian Institute for Health Information. All‐Cause Readmission to Acute Care and Return to the Emergency Department. Ottawa, ON: Canadian Institute for Health Information; 2012:1–64.
- , , . LACE+ index: extension of a validated index to predict early death or unplanned readmission following hospital discharge using administrative data. Open Medicine. 2012;6(2):80–89.
- . PCCF Plus version 5E user's guide. Ottawa ON: Statistics Canada; 2009;82F0086‐XDB.
- , , . Derivation and validation of diagnostic score based on case‐mix groups to predict 30‐day death or urgent readmission. Open Medicine. 2012;6(3):e80–e89.
- , . Executing high‐quality care transitions: a call to do it right. J Hosp Med. 2007;2(5):287–290.
- , , , . Predicting post‐discharge death or readmission: deterioration of model performance in a population having multiple admissions per patient [published online ahead of print November 19, 2012]. J Eval Clin Pract. doi: 10.1111/jep.12012.
- , , , . Patient self‐management of chronic disease in primary care. JAMA. 2002;288(19): 2469–2475.
- , . Multilevel analyses of neighbourhood socioeconomic context and health outcomes: a critical review. J Epidemiol Community Health. 2001;55(2):111–122.
- , , , et al. Incidence of potentially avoidable hospital readmissions and its relationship to all‐cause urgent readmissions. CMAJ. 2011;183(14):E1067–E1072.
- , , , . Validation of a combined comorbidity index. J Clin Epidemiol. 1994;47(11):1245–1251.
Socioeconomic status (SES) classifies people according to occupation, prior education, or income.[1] Socioeconomic status has been associated with several population‐health outcomes, albeit with geographically inconsistent results.[2] If lower SES is associated with higher readmission rates, then further studies could be done to determine which specific socioeconomic factors are potentially modifiable and whether the provision of additional resources could allay the increased risk associated with those factors.
Nine studies have examined the association between SES and readmissions.[3, 4, 5, 6, 7, 8, 9, 10, 11] These studies varied extensively in methodologies, SES measures, and results. However, results from 1 of these studies[11] were particularly notable given the study's significant association between lower household income and increased risk of acute readmission in a publicly funded, open‐access healthcare system. Given the implications of these results, an accurate and explicit assessment of the association between SES measures and the risk of adverse postdischarge outcomes is important.
We recently developed a model that accurately predicts the risk of 30‐day death or urgent readmission using administrative data.[12] This model did not directly control for any SES factors. In this study, we determined if a commonly used SES measurehousehold‐income quintilewas associated with the risk of early death or urgent readmission after controlling for factors known to influence this outcome.
METHODS
Study Setting and Data Sources
This population‐based study took place in Ontario, Canada, between April 1, 2003 and March 31, 2009. All hospital and physician care in Ontario is publicly funded. The study used 2 databases, the Discharge Abstract Database and the Registered Persons Database. The Discharge Abstract Database records information about all nonpsychiatric hospitalizations, including dates of hospital admission and discharge, vital status at end of hospitalization, discharge destination (ie, community, nursing home, or chronic hospital), admission urgency, primary and other diagnoses, and postal code of patient's household. The Registered Persons Database captures basic demographic data about all Ontarians, including date of birth and date of death (if applicable), postal code of residence, and average household‐income quintile of postal code, determined by linking the postal code to Statistics Canada geographical units through the Postal Code Conversion File Plus.[13] The Registered Persons Database captures all deaths regardless of the death location (ie, community vs hospital).
Study Population
This study used patients from a previous analysis that internally validated an index to predict the risk of 30‐day death or urgent readmission.[12] This analysis included a simple random sample of 250,000 adult Ontarians (age >18 years) who were discharged from the hospital to the community between April 1, 2003 and March 31, 2009. These medical and surgical hospitalizations were sampled from the Discharge Abstract Database described above. Psychiatric admissions were excluded because their hospitalizations are captured in a distinct database; obstetrical admissions were also excluded because they have a very low risk of 30‐day death or readmission. We randomly chose 1 index admission per person to ensure that the patient was the unit of analysis.
For the present study, we selected all patients from the previous analysis who were discharged from the hospital in 2006. This year was chosen because the SES indicator we used in the study (average household‐income quintile) was measured during the 2006 Canadian Census and would be most accurate for patients discharged in that year. The present study also limited patients to those with a valid postal code, because this was required to link patients to their neighborhood and their household‐income quintile.
Study Outcome
The study outcome was all‐cause death or urgent readmission within 30 days of discharge from hospital. We combined death with urgent readmission to avoid potential biases that could occur when measuring associations between risk factors and urgent readmission; in analyses having readmission as the sole outcome, the categorization of early deaths that occur prior to readmission as nonevents could minimize the importance of factors (such as severe comorbidities or patient age) that are associated with both early death and readmission.
We linked to the Registered Patients Database to determine each person's 30‐day death status. We linked to the Discharge Abstract Database to determine if patients had been urgently readmitted to any hospital within 30 days of discharge. All deaths were considered regardless of cause. All urgent (ie, nonscheduled) readmissions were included regardless of the reason for admission. Urgent status was determined by the urgency field in the Discharge Abstract Database, for which data abstractors are instructed to classify all nonscheduled admissions as urgent; these admissions frequently include those admitted after presenting to the emergency department.
Study Covariates: Readmission Risk and Neighborhood Household‐Income Quintile
In our primary analysis, we quantified the risk of 30‐day death or urgent readmission using an internally validated index, the LACE+ index: length of stay (L), acuity of the admission (A), comorbidity of the patient (measured with the Charlson Comorbidity Index score (C), and emergency‐department use (E).[12] The LACE+ index predicts the risk of 30‐day all‐cause death or urgent readmission for nonpsychiatric and nonobstetrical admissions. This index includes patient age, sex, comorbidities, and previous hospital and emergency‐department utilization; admission urgency; hospital type; total length of stay (LOS) and days in hospital awaiting placement; and hospitalization diagnostic risk.[14] The index quantified outcome risk as a score that ranged from 17 to 114. It was very discriminatory (C statistic, 77.1%) and was well calibrated (the observed and expected outcome risk was statistically distinct in only 2 of 14 risk groups that contained <2% of the population). The LACE+ quintiles were defined using score distribution from the entire 20032009 cohort.[12]
We used neighborhood income quintile as 1 measure of patient SES. Neighborhood income quintile was calculated by Statistics Canada using the Income Per Person Equivalent (IPPE) determined from the 2006 Canadian census.[13] The IPPE was calculated as total household income divided by the Single Persons Equivalent, which reflects decreased costs per person (and therefore increased available income per household occupant) in households having greater numbers of people. Within each dissemination area (each contains 400700 people), the average IPPE was calculated. Then, within each region (delineated by the Census Metropolitan Area, the Census Agglomeration, or provincial residual areas), dissemination areas were ranked by their average IPPE and then categorized into quintiles. These household‐income quintiles, therefore, are community‐specific and ensure that neighborhood household incomes are categorized based on comparisons within the same community. As such, the income thresholds for quintile categorization will vary between regions. We linked each patient's postal code to their dissemination area using the Postal Code Conversion File Plus[13] to determine their neighborhood income quintile.
Analysis
We described the patient cohort by readmission status. We categorized the expected risk of 30‐day death or urgent readmission to hospital (as determined by the LACE+ score) into quintiles. We used the 2 test and the test for trend to determine the association of these risk quintiles and SES quintiles with observed rates of 30‐day death or urgent readmission. The Cochran‐Mantel‐Haenszel test was used to determine the association of household‐income quintile and outcome risk after adjusting for LACE+ quintile.
To determine how the association between income quintile and outcome changes with increase adjustment, we constructed a series of logistic‐regression models that contained household‐income quintile and the sequential addition of components of the LACE+ score. For each model, we measured the influence of these added covariates on the association between household‐income quintile and early death or urgent readmission. We used orthogonal parameterization (which facilitates the comparison of parameter estimates in a regression model) to measure linear trends in the association of the income quintiles with outcomes.
RESULTS
The original cohort contained 250,000 people, of which 40,827 people (16.3%) were included in the present study (208,995 were excluded because patients were discharged in years other than 2006; 178 were excluded because of invalid postal codes).
Patients are described in Table 1. Patients were middle‐aged and had few documented chronic comorbidities. Of the patients, 37% had been to the emergency department and 12% had been admitted urgently. Most admissions were to large, nonteaching hospitals with a median LOS of 3 days.
| Variable | Value | No Death/Readmission, n=38,189 | Death/Readmission, n=2,638 | Overall, N=40,827 | |||
|---|---|---|---|---|---|---|---|
| |||||||
| Mean age (SD), y | 57.39 (18.3) | 67.17 (17.2) | 58.02 (18.4) | ||||
| Female sex | 20,044 | 52.5% | 1,291 | 48.9% | 21,335 | 52.3% | |
| Charlson index | 0 | 28,908 | 75.7% | 1,238 | 46.9% | 30,146 | 73.8% |
| 1 | 450 | 11.7% | 362 | 13.7% | 4,812 | 11.8% | |
| 2 | 2,668 | 7.0% | 427 | 16.2% | 3,095 | 7.6% | |
| 3+ | 2,163 | 5.7% | 611 | 23.2% | 2,774 | 6.8% | |
| ED visits in previous 6 moths | 0 | 24,599 | 64.4% | 1,210 | 45.9% | 25,809 | 63.2% |
| 12 | 11,262 | 29.5% | 1,008 | 38.2% | 12,270 | 30.1% | |
| 3+ | 2,328 | 6.1% | 420 | 15.9% | 2,748 | 6.7% | |
| Urgent hospitalizations, previous year | 0 | 33,729 | 88.3% | 1,796 | 68.1% | 35,525 | 87.0% |
| 1 | 3,425 | 9.0% | 525 | 19.9% | 3,950 | 9.7% | |
| 1+ | 1,035 | 2.7% | 317 | 12.0% | 1,352 | 3.3% | |
| Elective hospitalizations, previous year | 0 | 35,988 | 94.2% | 2,389 | 90.6% | 38,377 | 94.0% |
| 1 | 1,998 | 5.2% | 213 | 8.1% | 2,211 | 5.4% | |
| 2+ | 203 | 0.5% | 36 | 1.4% | 239 | 0.6% | |
| Hospital type | Nonteaching, large | 20,554 | 53.8% | 1,334 | 50.6% | 21,888 | 53.6% |
| Nonteaching, small | 5,239 | 13.7% | 487 | 18.5% | 5726 | 14.0% | |
| Teaching | 12,396 | 32.5% | 817 | 31.0% | 13,213 | 32.4% | |
| Urgent admit | 23,769 | 62.2% | 2,223 | 84.3% | 25,992 | 63.7% | |
| LOS rounded to nearest day, median (IQR) | 3 (26) | 5 (311) | 3 (26) | ||||
| Any hospital days on ALC | 0 | 646 | 1.7% | 127 | 4.8% | 773 | 1.9% |
| CMG score of index admission | 0 | 27,257 | 71.4% | 1,594 | 60.4% | 28,851 | 70.7% |
| 1+ | 5,218 | 13.7% | 948 | 35.9% | 6,166 | 15.1% | |
| <0 | 5,714 | 15.0% | 96 | 3.6% | 5,810 | 14.2% | |
| LACE+ score of index admission, median (IQR) | 31 (1848) | 61 (4175) | 32 (1951) | ||||
| Household‐income quintile | 1 (poorest) | 7,798 | 20.4% | 621 | 23.5% | 8,419 | 20.6% |
| 2 | 7,812 | 20.5% | 586 | 22.2% | 8,398 | 20.6% | |
| 3 | 7,557 | 19.8% | 484 | 18.3% | 8,041 | 19.7% | |
| 4 | 7,561 | 19.8% | 500 | 19.0% | 8,061 | 19.7% | |
| 5 (richest) | 7,461 | 19.5% | 447 | 16.9% | 7,908 | 19.4% | |
Death or urgent readmission within 30 days occurred in 2638 people (6.5%) (Table 1). Outcome risk increased with age; in males; as comorbidities increased; with greater numbers of emergency‐department visits, urgent admissions, and previous elective admissions; when index admissions were emergent; with longer hospital LOS and increased number of alternate level of care days; and as the diagnostic risk (measured as the Case Mix Group [CMG] score)[14] increased. Outcome risk increased as income quintile became poorer.
Household Income and Risk of 30‐Day Death or Urgent Readmission
People were evenly divided among the income quintiles (Table 2). By itself, household‐income quintile was significantly associated with the risk of early death or urgent hospital readmission (Table 2, column C, 2=27.4, P<0.0001; Mantel‐Haenszel trend 2=24.3, P<0.0001). In the poorest quintile, 7.4% of people had an outcome, compared with 5.6% in the richest quintile (2=19.8, df=1, P<0.0001).
| Risk Quintile of 30‐Day Death or Readmission (LACE+ Points Range) | ||||||
|---|---|---|---|---|---|---|
| 1 (1416) [A] | 2 (1727) | 3 (2839) | 4 (4056) | 5 (57114) [B] | Income Quintile Overall [C] | |
| ||||||
| Income quintile | ||||||
| 1 (poorest) | 18/1,485 (1.2%) | 42/1,667 (2.5%) | 65/1,635 (4.0%) | 117/1,722 (6.8%) | 379/1,910 (19.8%) | 621/8,419 (7.4%) |
| 2 | 21/1,627 (1.3%) | 39/1,665 (2.3%) | 65/1,598 (4.1%) | 130/1,808 (5.2%) | 331/1,700 (19.5%) | 586/8,398 (7.0%) |
| 3 | 18/1,761 (1.0%) | 33/1,665 (2.0%) | 63/1,568 (4.0%) | 96/1,499 (6.4%) | 274/1,548 (17.7%) | 484/8,041 (6.0%) |
| 4 | 27/1,851 (1.5%) | 42/1,698 (2.4%) | 57/1,585 (3.6%) | 110/1,548 (6.1%) | 264/1,379 (19.1%) | 500/8,061 (6.2%) |
| 5 (richest) | 20/1,864 (1.1%) | 32/1,736 (1.8%) | 60/1,468 (4.1%) | 107/1,525 (7.0%) | 228/1,315 (17.3%) | 447/7,908 (5.6%) |
| Risk quintile overall [D] | 104/8,588 (1.2%) | 188/8,431 (2.2%) | 310/7,854 (4.0%) | 560/8,102 (6.9%) | 1476/7,852 (18.8%) | 2,638/40,827 (6.5%) |
However, household income was also strongly associated with LACE+ scores (2=240, P<0.0001; Mantel‐Haenszel trend 2=209, P<0.0001). The number of people in the lowest‐risk quintile increased with income, from 1485 in the poorest quintile to 1864 in the richest quintile (Table 2, column A). In contrast, the number of high‐risk people progressively decreased with income, from 1910 in the poorest quintile to 1315 in the richest quintile (Table 2, column B).
The LACE+ quintile was very strongly associated with outcome risk, as shown in Table 2, row D (2=2703, P<0.0001; Mantel‐Haenszel trend 2=2102, P<0.0001). Within each LACE+ stratum, the risk of death or urgent readmission did not appear to consistently change with income quintile. After adjusting for LACE+ scores, income quintile was no longer associated with 30‐day death or readmission (Cochran‐Mantel‐Haenszel 2=5.9, df=4, P=0.21).
We found no nonlinear associations between household‐income quintile and 30‐day death or readmission after adjusting for the LACE+ score. In addition, the association between LACE+ quintile and outcome did not vary significantly by household‐income quintile (P value for interaction term in logistic regression model=0.5582).
The association between income quintile and 30‐day death or urgent readmission decreased when incrementally controlling for other covariates in the LACE+ model (Figure 1). By itself, all income quintiles except 2 were significantly distinct from the poorest income quintile. The addition of patient age, sex, and hospital type had little effect on the association between income and outcomes. The addition of index admission urgency shifted all point estimates toward unity (Figure 1). Associations between income and death or readmission then remained relatively stable until the addition of number of urgent admissions in the previous year (Figure 1). The subsequent addition of number of emergency visits and comorbidities resulted in none of the income quintiles being statistically distinct from the poorest quintile, as well as a nonsignificant linear trend over the quintiles.

DISCUSSION
Our study shows that the risk of 30‐day death or urgent readmission was higher in people from lower‐income neighborhoods. However, this risk appears to be explained by patient‐level factors that are known to be associated with bad postdischarge outcomes. After accounting for these factors with the LACE+ index, we found no notable changes in the risk of early death or urgent readmission with SES as measured with average neighborhood household income.
Nine previous studies have measured the association between various SES measures and hospital readmission in disparate populations.[3, 4, 5, 6, 7, 8, 9, 10, 11] These studies were done in the United States,[5, 6, 8, 9, 10] the United Kingdom,[3, 7] Australia,[4] and Canada.[11] They used a range of SES indicators (from area‐level measures of household income[5] or deprivation[3] to personal education and income)[8, 9, 10] in diverse patient populations (from a random sample of all hospitalizations[3] to people with disabilities living in New York City)[15] and very different time horizons (capturing hospital readmissions that occurred from within 30 days[5] to 4 years).[10] Of these 9 studies, 5 found no independent association between their SES measure and readmission,[5, 6, 8, 9, 10] and 2 included SES in their final regression model but did not present the modelmaking it impossible to determine if SES significantly influenced outcomes.[3, 15] One study found that the risk of hospital readmission independently increased as a composite measure of area‐level social and economic indicators decreased.[4] A Canadian study[11] measured neighborhood income quintile and showed, after adjusting for patient sex, comorbidities, LOS variance, and previous admissions, that the odds of acute, nonpsychiatric readmission within 30 days of discharge were approximately 10% higher in the lowest versus the highest SES quintile. The ability of this model to adjust for important confounders when associating SES and risk of readmission is uncertain because the model fit was not reported.
Several factors could explain the difference between our study and the previous Canadian analysis showing significantly higher adjusted risk of readmission in patients from the lowest versus the highest SES quintile.[11] First, our analysis had a slightly different outcome, combining early death with urgent readmission (rather than the latter alone). We believe that this combination is important to avoid biased results when associating patient factors with readmission risk.[14] Second, our unit of analysis was the patient, whereas in the previous analysis it was the hospitalization.[11] A recent analysis by our group found that this distinction can change the results on analyses in early postdischarge outcomes.[16] In the present analysis, different results could occur if patients with multiple readmissions were disproportionately prevalent in low‐income neighborhoods. Third, our analysis was limited to Ontario rather than the entire country. Finally, and we believe most importantly, we used a validated model to control for risk of poor outcomes soon after discharge from hospital. Our analysis shows that this risk was strongly associated with neighborhood income (Table 2). This suggests that the association between SES and bad postdischarge outcomes could be explained by factors that independently increase the risk of these outcomes. Adequately controlling for these covariates would then remove variation in readmission risk by SES. We believe that these results highlight the importance of adequately controlling for potential confounders.
We believe that our results are reassuring but not definitive. We found no indication that, in Ontario, people from poorer neighborhoods are systematically more likelyafter considering factors that are known to be associated with early death or urgent readmissionto have a worse outcome early after their discharge from hospital. However, patient income and other SES measures could be associated with early death or readmission for several reasons. First, our study used average neighborhood income quintiles to quantify SES. It is possible that other SES measures (such as education or social deprivation) or patient‐level SES indicators could be significantly associated with early death or readmission.[17, 18] Second, we previously found that approximately only 25% of hospital readmissions are potentially avoidable.[19] Further study is required to determine if patient SES independently influences potentially avoidable hospital readmissions. Third, we cannot be certain how our results might generalize to health populations outside of Ontario. Specifically, SES might play a more important role in regions without universal healthcare in which community‐based healthcare resources that could decrease readmission risk, such as medications or physician follow‐up, are unavailable to those without health insurance coverage. Finally, we found notable confounding between neighborhood income quintile and factors known to be independently associated with early death or urgent readmission (Figure 1). This was especially prominent with index admission urgency, number of previous urgent admissions and emergency visits, and patient comorbidities. These factors have a much stronger association with early death or readmission than neighborhood income quintile. If low neighborhood income actually results in urgent hospital admission, emergency‐department visits, and comorbidities, then the inclusion of these covariates in the model could obscure the influence of neighborhood income on early death or readmission.
In summary, our study found that neighborhood income was not associated with early death or urgent readmission independent of known risk factors. Our analysis indicates that focusing resources on patients in lower‐income neighborhoods is unlikely to change the risk of early postdischarge adverse events. Further study is required to determine if SES is associated with adverse postdischarge outcomes in settings without publicly funded healthcare.
Acknowledgment
Disclosure: Nothing to report.
Socioeconomic status (SES) classifies people according to occupation, prior education, or income.[1] Socioeconomic status has been associated with several population‐health outcomes, albeit with geographically inconsistent results.[2] If lower SES is associated with higher readmission rates, then further studies could be done to determine which specific socioeconomic factors are potentially modifiable and whether the provision of additional resources could allay the increased risk associated with those factors.
Nine studies have examined the association between SES and readmissions.[3, 4, 5, 6, 7, 8, 9, 10, 11] These studies varied extensively in methodologies, SES measures, and results. However, results from 1 of these studies[11] were particularly notable given the study's significant association between lower household income and increased risk of acute readmission in a publicly funded, open‐access healthcare system. Given the implications of these results, an accurate and explicit assessment of the association between SES measures and the risk of adverse postdischarge outcomes is important.
We recently developed a model that accurately predicts the risk of 30‐day death or urgent readmission using administrative data.[12] This model did not directly control for any SES factors. In this study, we determined if a commonly used SES measurehousehold‐income quintilewas associated with the risk of early death or urgent readmission after controlling for factors known to influence this outcome.
METHODS
Study Setting and Data Sources
This population‐based study took place in Ontario, Canada, between April 1, 2003 and March 31, 2009. All hospital and physician care in Ontario is publicly funded. The study used 2 databases, the Discharge Abstract Database and the Registered Persons Database. The Discharge Abstract Database records information about all nonpsychiatric hospitalizations, including dates of hospital admission and discharge, vital status at end of hospitalization, discharge destination (ie, community, nursing home, or chronic hospital), admission urgency, primary and other diagnoses, and postal code of patient's household. The Registered Persons Database captures basic demographic data about all Ontarians, including date of birth and date of death (if applicable), postal code of residence, and average household‐income quintile of postal code, determined by linking the postal code to Statistics Canada geographical units through the Postal Code Conversion File Plus.[13] The Registered Persons Database captures all deaths regardless of the death location (ie, community vs hospital).
Study Population
This study used patients from a previous analysis that internally validated an index to predict the risk of 30‐day death or urgent readmission.[12] This analysis included a simple random sample of 250,000 adult Ontarians (age >18 years) who were discharged from the hospital to the community between April 1, 2003 and March 31, 2009. These medical and surgical hospitalizations were sampled from the Discharge Abstract Database described above. Psychiatric admissions were excluded because their hospitalizations are captured in a distinct database; obstetrical admissions were also excluded because they have a very low risk of 30‐day death or readmission. We randomly chose 1 index admission per person to ensure that the patient was the unit of analysis.
For the present study, we selected all patients from the previous analysis who were discharged from the hospital in 2006. This year was chosen because the SES indicator we used in the study (average household‐income quintile) was measured during the 2006 Canadian Census and would be most accurate for patients discharged in that year. The present study also limited patients to those with a valid postal code, because this was required to link patients to their neighborhood and their household‐income quintile.
Study Outcome
The study outcome was all‐cause death or urgent readmission within 30 days of discharge from hospital. We combined death with urgent readmission to avoid potential biases that could occur when measuring associations between risk factors and urgent readmission; in analyses having readmission as the sole outcome, the categorization of early deaths that occur prior to readmission as nonevents could minimize the importance of factors (such as severe comorbidities or patient age) that are associated with both early death and readmission.
We linked to the Registered Patients Database to determine each person's 30‐day death status. We linked to the Discharge Abstract Database to determine if patients had been urgently readmitted to any hospital within 30 days of discharge. All deaths were considered regardless of cause. All urgent (ie, nonscheduled) readmissions were included regardless of the reason for admission. Urgent status was determined by the urgency field in the Discharge Abstract Database, for which data abstractors are instructed to classify all nonscheduled admissions as urgent; these admissions frequently include those admitted after presenting to the emergency department.
Study Covariates: Readmission Risk and Neighborhood Household‐Income Quintile
In our primary analysis, we quantified the risk of 30‐day death or urgent readmission using an internally validated index, the LACE+ index: length of stay (L), acuity of the admission (A), comorbidity of the patient (measured with the Charlson Comorbidity Index score (C), and emergency‐department use (E).[12] The LACE+ index predicts the risk of 30‐day all‐cause death or urgent readmission for nonpsychiatric and nonobstetrical admissions. This index includes patient age, sex, comorbidities, and previous hospital and emergency‐department utilization; admission urgency; hospital type; total length of stay (LOS) and days in hospital awaiting placement; and hospitalization diagnostic risk.[14] The index quantified outcome risk as a score that ranged from 17 to 114. It was very discriminatory (C statistic, 77.1%) and was well calibrated (the observed and expected outcome risk was statistically distinct in only 2 of 14 risk groups that contained <2% of the population). The LACE+ quintiles were defined using score distribution from the entire 20032009 cohort.[12]
We used neighborhood income quintile as 1 measure of patient SES. Neighborhood income quintile was calculated by Statistics Canada using the Income Per Person Equivalent (IPPE) determined from the 2006 Canadian census.[13] The IPPE was calculated as total household income divided by the Single Persons Equivalent, which reflects decreased costs per person (and therefore increased available income per household occupant) in households having greater numbers of people. Within each dissemination area (each contains 400700 people), the average IPPE was calculated. Then, within each region (delineated by the Census Metropolitan Area, the Census Agglomeration, or provincial residual areas), dissemination areas were ranked by their average IPPE and then categorized into quintiles. These household‐income quintiles, therefore, are community‐specific and ensure that neighborhood household incomes are categorized based on comparisons within the same community. As such, the income thresholds for quintile categorization will vary between regions. We linked each patient's postal code to their dissemination area using the Postal Code Conversion File Plus[13] to determine their neighborhood income quintile.
Analysis
We described the patient cohort by readmission status. We categorized the expected risk of 30‐day death or urgent readmission to hospital (as determined by the LACE+ score) into quintiles. We used the 2 test and the test for trend to determine the association of these risk quintiles and SES quintiles with observed rates of 30‐day death or urgent readmission. The Cochran‐Mantel‐Haenszel test was used to determine the association of household‐income quintile and outcome risk after adjusting for LACE+ quintile.
To determine how the association between income quintile and outcome changes with increase adjustment, we constructed a series of logistic‐regression models that contained household‐income quintile and the sequential addition of components of the LACE+ score. For each model, we measured the influence of these added covariates on the association between household‐income quintile and early death or urgent readmission. We used orthogonal parameterization (which facilitates the comparison of parameter estimates in a regression model) to measure linear trends in the association of the income quintiles with outcomes.
RESULTS
The original cohort contained 250,000 people, of which 40,827 people (16.3%) were included in the present study (208,995 were excluded because patients were discharged in years other than 2006; 178 were excluded because of invalid postal codes).
Patients are described in Table 1. Patients were middle‐aged and had few documented chronic comorbidities. Of the patients, 37% had been to the emergency department and 12% had been admitted urgently. Most admissions were to large, nonteaching hospitals with a median LOS of 3 days.
| Variable | Value | No Death/Readmission, n=38,189 | Death/Readmission, n=2,638 | Overall, N=40,827 | |||
|---|---|---|---|---|---|---|---|
| |||||||
| Mean age (SD), y | 57.39 (18.3) | 67.17 (17.2) | 58.02 (18.4) | ||||
| Female sex | 20,044 | 52.5% | 1,291 | 48.9% | 21,335 | 52.3% | |
| Charlson index | 0 | 28,908 | 75.7% | 1,238 | 46.9% | 30,146 | 73.8% |
| 1 | 450 | 11.7% | 362 | 13.7% | 4,812 | 11.8% | |
| 2 | 2,668 | 7.0% | 427 | 16.2% | 3,095 | 7.6% | |
| 3+ | 2,163 | 5.7% | 611 | 23.2% | 2,774 | 6.8% | |
| ED visits in previous 6 moths | 0 | 24,599 | 64.4% | 1,210 | 45.9% | 25,809 | 63.2% |
| 12 | 11,262 | 29.5% | 1,008 | 38.2% | 12,270 | 30.1% | |
| 3+ | 2,328 | 6.1% | 420 | 15.9% | 2,748 | 6.7% | |
| Urgent hospitalizations, previous year | 0 | 33,729 | 88.3% | 1,796 | 68.1% | 35,525 | 87.0% |
| 1 | 3,425 | 9.0% | 525 | 19.9% | 3,950 | 9.7% | |
| 1+ | 1,035 | 2.7% | 317 | 12.0% | 1,352 | 3.3% | |
| Elective hospitalizations, previous year | 0 | 35,988 | 94.2% | 2,389 | 90.6% | 38,377 | 94.0% |
| 1 | 1,998 | 5.2% | 213 | 8.1% | 2,211 | 5.4% | |
| 2+ | 203 | 0.5% | 36 | 1.4% | 239 | 0.6% | |
| Hospital type | Nonteaching, large | 20,554 | 53.8% | 1,334 | 50.6% | 21,888 | 53.6% |
| Nonteaching, small | 5,239 | 13.7% | 487 | 18.5% | 5726 | 14.0% | |
| Teaching | 12,396 | 32.5% | 817 | 31.0% | 13,213 | 32.4% | |
| Urgent admit | 23,769 | 62.2% | 2,223 | 84.3% | 25,992 | 63.7% | |
| LOS rounded to nearest day, median (IQR) | 3 (26) | 5 (311) | 3 (26) | ||||
| Any hospital days on ALC | 0 | 646 | 1.7% | 127 | 4.8% | 773 | 1.9% |
| CMG score of index admission | 0 | 27,257 | 71.4% | 1,594 | 60.4% | 28,851 | 70.7% |
| 1+ | 5,218 | 13.7% | 948 | 35.9% | 6,166 | 15.1% | |
| <0 | 5,714 | 15.0% | 96 | 3.6% | 5,810 | 14.2% | |
| LACE+ score of index admission, median (IQR) | 31 (1848) | 61 (4175) | 32 (1951) | ||||
| Household‐income quintile | 1 (poorest) | 7,798 | 20.4% | 621 | 23.5% | 8,419 | 20.6% |
| 2 | 7,812 | 20.5% | 586 | 22.2% | 8,398 | 20.6% | |
| 3 | 7,557 | 19.8% | 484 | 18.3% | 8,041 | 19.7% | |
| 4 | 7,561 | 19.8% | 500 | 19.0% | 8,061 | 19.7% | |
| 5 (richest) | 7,461 | 19.5% | 447 | 16.9% | 7,908 | 19.4% | |
Death or urgent readmission within 30 days occurred in 2638 people (6.5%) (Table 1). Outcome risk increased with age; in males; as comorbidities increased; with greater numbers of emergency‐department visits, urgent admissions, and previous elective admissions; when index admissions were emergent; with longer hospital LOS and increased number of alternate level of care days; and as the diagnostic risk (measured as the Case Mix Group [CMG] score)[14] increased. Outcome risk increased as income quintile became poorer.
Household Income and Risk of 30‐Day Death or Urgent Readmission
People were evenly divided among the income quintiles (Table 2). By itself, household‐income quintile was significantly associated with the risk of early death or urgent hospital readmission (Table 2, column C, 2=27.4, P<0.0001; Mantel‐Haenszel trend 2=24.3, P<0.0001). In the poorest quintile, 7.4% of people had an outcome, compared with 5.6% in the richest quintile (2=19.8, df=1, P<0.0001).
| Risk Quintile of 30‐Day Death or Readmission (LACE+ Points Range) | ||||||
|---|---|---|---|---|---|---|
| 1 (1416) [A] | 2 (1727) | 3 (2839) | 4 (4056) | 5 (57114) [B] | Income Quintile Overall [C] | |
| ||||||
| Income quintile | ||||||
| 1 (poorest) | 18/1,485 (1.2%) | 42/1,667 (2.5%) | 65/1,635 (4.0%) | 117/1,722 (6.8%) | 379/1,910 (19.8%) | 621/8,419 (7.4%) |
| 2 | 21/1,627 (1.3%) | 39/1,665 (2.3%) | 65/1,598 (4.1%) | 130/1,808 (5.2%) | 331/1,700 (19.5%) | 586/8,398 (7.0%) |
| 3 | 18/1,761 (1.0%) | 33/1,665 (2.0%) | 63/1,568 (4.0%) | 96/1,499 (6.4%) | 274/1,548 (17.7%) | 484/8,041 (6.0%) |
| 4 | 27/1,851 (1.5%) | 42/1,698 (2.4%) | 57/1,585 (3.6%) | 110/1,548 (6.1%) | 264/1,379 (19.1%) | 500/8,061 (6.2%) |
| 5 (richest) | 20/1,864 (1.1%) | 32/1,736 (1.8%) | 60/1,468 (4.1%) | 107/1,525 (7.0%) | 228/1,315 (17.3%) | 447/7,908 (5.6%) |
| Risk quintile overall [D] | 104/8,588 (1.2%) | 188/8,431 (2.2%) | 310/7,854 (4.0%) | 560/8,102 (6.9%) | 1476/7,852 (18.8%) | 2,638/40,827 (6.5%) |
However, household income was also strongly associated with LACE+ scores (2=240, P<0.0001; Mantel‐Haenszel trend 2=209, P<0.0001). The number of people in the lowest‐risk quintile increased with income, from 1485 in the poorest quintile to 1864 in the richest quintile (Table 2, column A). In contrast, the number of high‐risk people progressively decreased with income, from 1910 in the poorest quintile to 1315 in the richest quintile (Table 2, column B).
The LACE+ quintile was very strongly associated with outcome risk, as shown in Table 2, row D (2=2703, P<0.0001; Mantel‐Haenszel trend 2=2102, P<0.0001). Within each LACE+ stratum, the risk of death or urgent readmission did not appear to consistently change with income quintile. After adjusting for LACE+ scores, income quintile was no longer associated with 30‐day death or readmission (Cochran‐Mantel‐Haenszel 2=5.9, df=4, P=0.21).
We found no nonlinear associations between household‐income quintile and 30‐day death or readmission after adjusting for the LACE+ score. In addition, the association between LACE+ quintile and outcome did not vary significantly by household‐income quintile (P value for interaction term in logistic regression model=0.5582).
The association between income quintile and 30‐day death or urgent readmission decreased when incrementally controlling for other covariates in the LACE+ model (Figure 1). By itself, all income quintiles except 2 were significantly distinct from the poorest income quintile. The addition of patient age, sex, and hospital type had little effect on the association between income and outcomes. The addition of index admission urgency shifted all point estimates toward unity (Figure 1). Associations between income and death or readmission then remained relatively stable until the addition of number of urgent admissions in the previous year (Figure 1). The subsequent addition of number of emergency visits and comorbidities resulted in none of the income quintiles being statistically distinct from the poorest quintile, as well as a nonsignificant linear trend over the quintiles.

DISCUSSION
Our study shows that the risk of 30‐day death or urgent readmission was higher in people from lower‐income neighborhoods. However, this risk appears to be explained by patient‐level factors that are known to be associated with bad postdischarge outcomes. After accounting for these factors with the LACE+ index, we found no notable changes in the risk of early death or urgent readmission with SES as measured with average neighborhood household income.
Nine previous studies have measured the association between various SES measures and hospital readmission in disparate populations.[3, 4, 5, 6, 7, 8, 9, 10, 11] These studies were done in the United States,[5, 6, 8, 9, 10] the United Kingdom,[3, 7] Australia,[4] and Canada.[11] They used a range of SES indicators (from area‐level measures of household income[5] or deprivation[3] to personal education and income)[8, 9, 10] in diverse patient populations (from a random sample of all hospitalizations[3] to people with disabilities living in New York City)[15] and very different time horizons (capturing hospital readmissions that occurred from within 30 days[5] to 4 years).[10] Of these 9 studies, 5 found no independent association between their SES measure and readmission,[5, 6, 8, 9, 10] and 2 included SES in their final regression model but did not present the modelmaking it impossible to determine if SES significantly influenced outcomes.[3, 15] One study found that the risk of hospital readmission independently increased as a composite measure of area‐level social and economic indicators decreased.[4] A Canadian study[11] measured neighborhood income quintile and showed, after adjusting for patient sex, comorbidities, LOS variance, and previous admissions, that the odds of acute, nonpsychiatric readmission within 30 days of discharge were approximately 10% higher in the lowest versus the highest SES quintile. The ability of this model to adjust for important confounders when associating SES and risk of readmission is uncertain because the model fit was not reported.
Several factors could explain the difference between our study and the previous Canadian analysis showing significantly higher adjusted risk of readmission in patients from the lowest versus the highest SES quintile.[11] First, our analysis had a slightly different outcome, combining early death with urgent readmission (rather than the latter alone). We believe that this combination is important to avoid biased results when associating patient factors with readmission risk.[14] Second, our unit of analysis was the patient, whereas in the previous analysis it was the hospitalization.[11] A recent analysis by our group found that this distinction can change the results on analyses in early postdischarge outcomes.[16] In the present analysis, different results could occur if patients with multiple readmissions were disproportionately prevalent in low‐income neighborhoods. Third, our analysis was limited to Ontario rather than the entire country. Finally, and we believe most importantly, we used a validated model to control for risk of poor outcomes soon after discharge from hospital. Our analysis shows that this risk was strongly associated with neighborhood income (Table 2). This suggests that the association between SES and bad postdischarge outcomes could be explained by factors that independently increase the risk of these outcomes. Adequately controlling for these covariates would then remove variation in readmission risk by SES. We believe that these results highlight the importance of adequately controlling for potential confounders.
We believe that our results are reassuring but not definitive. We found no indication that, in Ontario, people from poorer neighborhoods are systematically more likelyafter considering factors that are known to be associated with early death or urgent readmissionto have a worse outcome early after their discharge from hospital. However, patient income and other SES measures could be associated with early death or readmission for several reasons. First, our study used average neighborhood income quintiles to quantify SES. It is possible that other SES measures (such as education or social deprivation) or patient‐level SES indicators could be significantly associated with early death or readmission.[17, 18] Second, we previously found that approximately only 25% of hospital readmissions are potentially avoidable.[19] Further study is required to determine if patient SES independently influences potentially avoidable hospital readmissions. Third, we cannot be certain how our results might generalize to health populations outside of Ontario. Specifically, SES might play a more important role in regions without universal healthcare in which community‐based healthcare resources that could decrease readmission risk, such as medications or physician follow‐up, are unavailable to those without health insurance coverage. Finally, we found notable confounding between neighborhood income quintile and factors known to be independently associated with early death or urgent readmission (Figure 1). This was especially prominent with index admission urgency, number of previous urgent admissions and emergency visits, and patient comorbidities. These factors have a much stronger association with early death or readmission than neighborhood income quintile. If low neighborhood income actually results in urgent hospital admission, emergency‐department visits, and comorbidities, then the inclusion of these covariates in the model could obscure the influence of neighborhood income on early death or readmission.
In summary, our study found that neighborhood income was not associated with early death or urgent readmission independent of known risk factors. Our analysis indicates that focusing resources on patients in lower‐income neighborhoods is unlikely to change the risk of early postdischarge adverse events. Further study is required to determine if SES is associated with adverse postdischarge outcomes in settings without publicly funded healthcare.
Acknowledgment
Disclosure: Nothing to report.
- Last JM, ed. A Dictionary of Epidemiology. 3rd ed. New York, NY: Oxford University Press; 1995.
- , , , et al. Is income inequality a determinant of population health? Part 1: A systematic review. Milbank Q. 2004;82(1):5–99.
- , , . Identifying patients at high risk of emergency hospital admissions: a logistic regression analysis. J R Soc Med. 2006;99(8):406–414.
- , , , . Using routine inpatient data to identify patients at risk of hospital readmission. BMC Health Serv Res. 2009;9:96.
- , , , , . Risk factors for 30‐day hospital readmission in patients ≥65 years of age. Proc (Bayl Univ Med Cent). 2008;21(4):363–372.
- , , , et al. An automated model to identify heart failure patients at risk for 30‐day readmission or death using electronic medical record data. Med Care. 2010;48(11):981–988.
- , . Improving the management of care for high‐cost Medicaid patients. Health Aff (Millwood). 2007;26(6):1643–1654.
- , . Factors predicting readmission of older general medicine patients. J Gen Intern Med. 1991;6(5):389–393.
- , , , et al. Hospital readmission in general medicine patients: a prediction model. J Gen Intern Med. 2010;25(3):211–219.
- , , , , , . Screening elders for risk of hospital admission. J Am Geriatr Soc. 1993;41(8):811–817.
- Canadian Institute for Health Information. All‐Cause Readmission to Acute Care and Return to the Emergency Department. Ottawa, ON: Canadian Institute for Health Information; 2012:1–64.
- , , . LACE+ index: extension of a validated index to predict early death or unplanned readmission following hospital discharge using administrative data. Open Medicine. 2012;6(2):80–89.
- . PCCF Plus version 5E user's guide. Ottawa ON: Statistics Canada; 2009;82F0086‐XDB.
- , , . Derivation and validation of diagnostic score based on case‐mix groups to predict 30‐day death or urgent readmission. Open Medicine. 2012;6(3):e80–e89.
- , . Executing high‐quality care transitions: a call to do it right. J Hosp Med. 2007;2(5):287–290.
- , , , . Predicting post‐discharge death or readmission: deterioration of model performance in a population having multiple admissions per patient [published online ahead of print November 19, 2012]. J Eval Clin Pract. doi: 10.1111/jep.12012.
- , , , . Patient self‐management of chronic disease in primary care. JAMA. 2002;288(19): 2469–2475.
- , . Multilevel analyses of neighbourhood socioeconomic context and health outcomes: a critical review. J Epidemiol Community Health. 2001;55(2):111–122.
- , , , et al. Incidence of potentially avoidable hospital readmissions and its relationship to all‐cause urgent readmissions. CMAJ. 2011;183(14):E1067–E1072.
- , , , . Validation of a combined comorbidity index. J Clin Epidemiol. 1994;47(11):1245–1251.
- Last JM, ed. A Dictionary of Epidemiology. 3rd ed. New York, NY: Oxford University Press; 1995.
- , , , et al. Is income inequality a determinant of population health? Part 1: A systematic review. Milbank Q. 2004;82(1):5–99.
- , , . Identifying patients at high risk of emergency hospital admissions: a logistic regression analysis. J R Soc Med. 2006;99(8):406–414.
- , , , . Using routine inpatient data to identify patients at risk of hospital readmission. BMC Health Serv Res. 2009;9:96.
- , , , , . Risk factors for 30‐day hospital readmission in patients ≥65 years of age. Proc (Bayl Univ Med Cent). 2008;21(4):363–372.
- , , , et al. An automated model to identify heart failure patients at risk for 30‐day readmission or death using electronic medical record data. Med Care. 2010;48(11):981–988.
- , . Improving the management of care for high‐cost Medicaid patients. Health Aff (Millwood). 2007;26(6):1643–1654.
- , . Factors predicting readmission of older general medicine patients. J Gen Intern Med. 1991;6(5):389–393.
- , , , et al. Hospital readmission in general medicine patients: a prediction model. J Gen Intern Med. 2010;25(3):211–219.
- , , , , , . Screening elders for risk of hospital admission. J Am Geriatr Soc. 1993;41(8):811–817.
- Canadian Institute for Health Information. All‐Cause Readmission to Acute Care and Return to the Emergency Department. Ottawa, ON: Canadian Institute for Health Information; 2012:1–64.
- , , . LACE+ index: extension of a validated index to predict early death or unplanned readmission following hospital discharge using administrative data. Open Medicine. 2012;6(2):80–89.
- . PCCF Plus version 5E user's guide. Ottawa ON: Statistics Canada; 2009;82F0086‐XDB.
- , , . Derivation and validation of diagnostic score based on case‐mix groups to predict 30‐day death or urgent readmission. Open Medicine. 2012;6(3):e80–e89.
- , . Executing high‐quality care transitions: a call to do it right. J Hosp Med. 2007;2(5):287–290.
- , , , . Predicting post‐discharge death or readmission: deterioration of model performance in a population having multiple admissions per patient [published online ahead of print November 19, 2012]. J Eval Clin Pract. doi: 10.1111/jep.12012.
- , , , . Patient self‐management of chronic disease in primary care. JAMA. 2002;288(19): 2469–2475.
- , . Multilevel analyses of neighbourhood socioeconomic context and health outcomes: a critical review. J Epidemiol Community Health. 2001;55(2):111–122.
- , , , et al. Incidence of potentially avoidable hospital readmissions and its relationship to all‐cause urgent readmissions. CMAJ. 2011;183(14):E1067–E1072.
- , , , . Validation of a combined comorbidity index. J Clin Epidemiol. 1994;47(11):1245–1251.
Copyright © 2013 Society of Hospital Medicine