User login
Proximal Humerus Fracture 3-D Modeling
ABSTRACT
The objective of this study is to determine the reproducibility and feasibility of using 3-dimensional (3-D) computer simulation of proximal humerus fracture computed tomography (CT) scans for fracture reduction. We hypothesized that anatomic reconstruction with 3-D models would be anatomically accurate and reproducible.
Preoperative CT scans of 28 patients with 3- and 4-part (AO classification 11-B1, 11-B2, 11-C1, 11-C2) proximal humerus fractures who were treated by hemiarthroplasty were converted into 3-D computer models. The displaced fractured fragments were anatomically reduced with computer simulation by 2 fellowship-trained shoulder surgeons, and measurements were made of the reconstructed proximal humerus.
The measurements of the reconstructed models had very good to excellent interobserver and intraobserver reliability. The reconstructions of these humerus fractures showed interclass correlation coefficients ranging from 0.71 to 0.93 between 1 observer and from 0.82 to 0.98 between 2 different observers. The fracture reduction was judged against normal proximal humerus geometry to determine reduction accuracy.
The 3-D modeling techniques used to reconstruct 3- and 4-part proximal humerus fractures were reliable and accurate. This technique of modeling and reconstructing proximal humerus fractures could be used to enhance the preoperative planning of open reduction and internal fixation or hemiarthroplasty for 3- and 4-part proximal humerus fractures.
The treatment of proximal humerus fractures is influenced by multiple factors, including patient age, associated injuries, bone quality, and fracture pattern. Three- and 4-part fractures are among the more severe of these fractures, which may result in vascular compromise to the humeral head, leading to avascular necrosis. Surgical goals for the management of these fractures are to optimize functional outcomes by re-creating a stable construct with a functional rotator cuff by open reduction and internal fixation (ORIF), hemiarthroplasty with tuberosity ORIF, or reverse shoulder replacement. Achieving a good outcome following hemiarthroplasty is dependent on many factors, including anatomic tuberosity healing and component positioning.1,2,3 Repairing the greater tuberosity in a near-anatomic position has been shown to greatly affect the results of hemiarthroplasty for fracture.3,4
Continue to: Three-dimensional (3-D) modeling...
Three-dimensional (3-D) modeling is increasingly being used in preoperative planning of shoulder arthroplasty and determining proper proximal humeral fracture treatment. 5 However, no studies have examined the reconstruction of a fractured proximal humerus into native anatomy using computer simulation. The purpose of this study is to determine the accuracy and reliability of anatomically reconstructing the preinjury proximal humerus using 3-D computer models created from postinjury computed tomography (CT) scans. The results of this study could lead to useful techniques employing CT–based models for patient-specific preoperative planning of proximal humeral fracture ORIF and during tuberosity reduction and fixation during hemiarthroplasty for fracture. We hypothesize that it is feasible to reconstruct the original anatomy of the proximal humerus by using 3-D computer modeling of proximal humerus fractures with high reliability based on interobserver and intraobserver review.
METHODS
After Institutional Review Board approval was obtained, we reviewed the medical records of consecutive patients with a diagnosis of proximal humeral fracture and the treatment codes for hemiarthroplasty from 2000 to 2013. Inclusion criteria included 3- and 4-part fractures (AO classifications 11-B1, 11-B2, 11-C1, 11-C2). CT scans with insufficient quality to differentiate bone from soft tissue (inadequate signal-to-noise ratio) were excluded from the study. A total of 28 patients with adequate CT scans met the criteria for inclusion in this study.
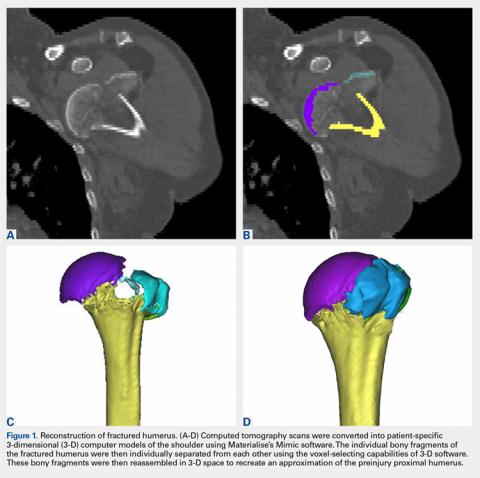
The CT scan protocol included 0.5-mm axial cuts with inclusion of the proximal humerus in the Digital Imaging and Communications in Medicine format. These CT scans were converted into patient-specific 3-D computer models of the shoulder using Mimics software (Materialise Inc.). The use of this software to produce anatomically accurate models has previously been verified in a shoulder model.6,7 The tuberosity fragments were then individually separated from each other using the voxel-selecting capabilities of 3-D software and manipulated with translation and rotation for anatomic reduction (Figures 1A-1D, Figure 2).
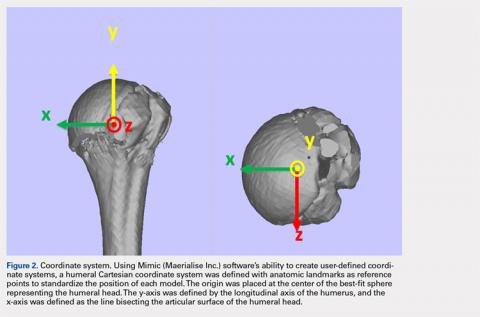
The de-identified anatomically reconstructed shoulder models were then uploaded into Materialise’s Magics rapid prototyping software, and a user-defined humeral Cartesian coordinate system was defined with anatomic landmarks as reference points to standardize the position of each model (Figure 3).8,9
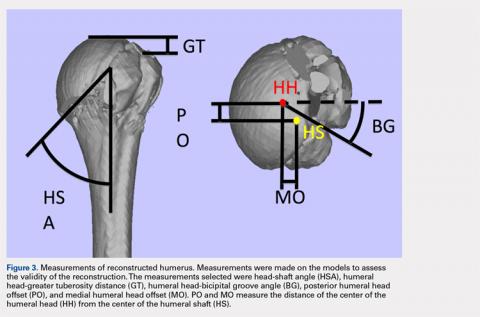
A series of measurements were made on these models to assess the validity and reliability of the reassembly. The bicipital groove at the anatomic neck was used to measure humeral head version as described by Kummer and colleagues.10 The head-shaft angle, humeral head-greater tuberosity distance, humeral head-bicipital groove angle, and posterior and medial humeral head offset were measured directly on the reconstructed humerus.
Continue to: Two fellowship-trained shoulder...
Two fellowship-trained shoulder surgeons independently reassembled these fracture fragments via computer simulation. Interobserver reliability testing was conducted on these reconstructions by measuring the geometry between the 2 different surgeons’ reconstructions. Intraobserver reliability testing was conducted by 1 surgeon repeating the reconstructions with 4-week intervals between trials and measuring the geometry between the 2 different trials. The average dimensions of the reconstructed proximal humerus fractures were compared with the geometry of normal humeri reported in previously conducted anatomic studies.11,12,13
STATISTICS
The measured dimensions of the 28 reassembled proximal humeri models were averaged across all trials between the 2 fellowship-trained surgeons and compared with the range of normal dimensions of a healthy proximal humerus using the 2 one-sided tests (TOST) method for equivalence between 2 means given a range. The interobserver and intraobserver reliabilities were quantified using the interclass correlation coefficient. An excellent correlation was defined as a correlation coefficient >0.81; very good was defined as 0.61 to 0.80; and good was defined as 0.41 to 0.60.
RESULTS
Of the patients studied, 9 (32.1%) were male, and the average age at the time of CT scanning was 72 years. Of the 28 patients with fracture, 18 (64.2%) had 3-part fractures (AO classifications 11-B1, 11-B2), and 10 (35.8%) had 4-part fractures (AO classifications 11-C1, 11-C2). When examining the location of the intertubercular fracture line, we found that 13 (46.4%) fractures went through the bicipital groove. Of the remaining fracture lines, 9 (32.1%) extended into the greater tuberosity and 6 (21.4%) extended into the lesser tuberosity.
All users were able to reconstruct all 28 fractures using this technique. The average measured dimensions fell within the range of dimensions of a normal healthy proximal humerus specified in the literature to within a 95% confidence interval using the TOST for equivalence, in which we compared measured values with ranges reported in the literature (Table).11,12,13
Table. Dimensions of Proximal Humerus Geometry
| Normal Parameters | Average Dimensions From Trials | Dimensions From Literature |
| Head shaft angle | 43.5° ± 1° | 42.5° ± 12.5° |
| Head to greater tuberosity distance | 4.9 mm ± 0.4 mm | 8 mm ± 3.2 mm |
Head to bicipital groove angle (anatomic neck) | 26.4° ± 2° | 27.3° ± 14° |
| Posterior humeral head offset | 1.6 mm ± 0.3 mm | 4 mm ± 6 mm |
| Medial humeral head offset | 4.5 mm ± 0.3 mm | 9 mm ± 5 mm |
The reconstructions of these humerus fractures showed intraclass correlation coefficients ranging from 0.71 to 0.93 in 1 observer and interclass correlation coefficients from 0.82 to 0.98 between 2 different observers (Table).
DISCUSSION
This study demonstrates that it is feasible to reliably and accurately reconstruct the original anatomy of the proximal humerus by using 3-D computer modeling of proximal humerus fractures. Poor outcomes after hemiarthroplasty for proximal humerus fractures are mostly related to tuberosity malpositioning, resorption, or failure of fixation and resultant dysfunction of the rotator cuff.14,15,16 These studies highlight the importance of accurate tuberosity reduction during surgical care of these fractures.
Continue to: The 3-D computer model...
The 3-D computer model reconstruction of 3- and 4-part proximal humerus fractures were reliable and valid. The interclass correlation coefficients showed very good to excellent interobserver and intraobserver reliability for all measurements conducted. The averaged dimensions from all trials fell within the appropriate range of dimensions for a normal healthy humerus reported in the literature, as verified by the TOST method.11,12,13 The 3-D modeling capabilities demonstrated in this study allowed a greater understanding of the fracture patterns present in 3- and 4-part (AO classifications 11-B1, 11-B2, 11-C1, 11-C2) humerus fractures.
Overreduction of greater tuberosity to create cortical overlap with the lateral shaft may be used to promote bony union. As a result of this distalization, there may be extra strains placed on the rotator cuff, making the patient more prone to rotator cuff tear, as well as improperly balancing the dynamic stabilizers of the shoulder. Poor clinical outcomes in hemiarthroplasty for proximal humerus fractures have been correlated with a greater tuberosity placed distal relative to the humeral head by 1 cm in a study2 and by 2 cm in another.3
This study has several limitations. The first is the assumption that our injured patients had preinjury proximal humerus geometry within the range of normal dimensions of a healthy humerus. Unfortunately, because we were unable to obtain CT scans of the contralateral shoulder, we had to use standard proximal humerus geometry as the control. Another limitation, inherent in the technique, is that only cortical and dense trabecular bone was modeled, so that comminuted or osteoporotic bone was not well modeled. This study did not correlate the findings from these models with clinical outcomes. A prospective study is needed to evaluate the impact of this 3-D modeling on fracture reductions and clinical outcomes.
This study demonstrates that patient-specific modeling of proximal humerus fracture 3-D CT scans may help surgeons reliably and accurately reconstruct fractures. This technique may have utility in the preoperative planning of tuberosity fracture reduction and hemiarthroplasty. It gives surgeons the ability to visualize fracture fragments, and the process of reconstructing the fragments may help surgeons understand the required maneuvers for reduction at the time of surgery. This technique also provides dimensions of the patient’s native humerus, thus potentially improving the anatomic accuracy of the reduction or hemiarthroplasty reconstruction. With the new trend toward patient-specific instrumentation, this study also provides a means of planning the size of the humeral prostheses as well as the version relative to the biceps groove and intertubercular fracture line.
CONCLUSION
This study demonstrates the feasibility of using 3-D computer modeling of complex proximal humerus fractures in anatomic reconstruction. These techniques of computer-simulated 3-D models are valid and reliable. We believe that this technique of modeling and reconstructing proximal humerus fractures could be used to enhance the preoperative planning of hemiarthroplasty for 3- and 4-part proximal humerus fractures by providing improved understanding of the patient’s native humeral geometry and tuberosity reduction.
1. Boileau P, Krishnan SG, Tinsi L, Walch G, Coste JS, Mole D. Tuberosity malposition and migration: reasons for poor outcomes after hemiarthroplasty for displaced fractures of the proximal humerus. J Shoulder Elbow Surg. 2002;11(5):401-412. doi:10.1067/mse.2002.124527.
2. Mighell MA, Kolm GP, Collinge CA, Frankle MA. Outcomes of hemiarthroplasty for fractures of the proximal humerus. J Shoulder Elbow Surg. 2003;12(6):569-577. doi:10.1016/S1058274603002131.
3. Greiner SH, Kaab MJ, Kroning I, Scheibel M, Perka C. Reconstruction of humeral length and centering of the prosthetic head in hemiarthroplasty for proximal humeral fractures. J Shoulder Elbow Surg. 2008;17(5):709-714. doi:10.1016/j.jse.2008.03.004.
4. Smith AM, Mardones RM, Sperling JW, Cofield RH. Early complications of operatively treated proximal humeral fractures. J Shoulder Elbow Surg. 2007;16(1):14-24. doi:10.1016/j.jse.2006.05.008.
5. Scalise JJ, Codsi MJ, Bryan J, Iannotti JP. The three-dimensional glenoid vault model can estimate normal glenoid version in osteoarthritis. J Shoulder Elbow Surg. 2008;17(3):487-491. doi:10.1016/j.jse.2007.09.006.
6. Bryce CD, Pennypacker JL, Kulkarni N, et al. Validation of three-dimensional models of in situ scapulae. J Shoulder Elbow Surg. 2008;17(5):825-832. doi:10.1016/j.jse.2008.01.141.
7. Yongpravat C, Kim HM, Gardner TR, Bigliani LU, Levine WN, Ahmad CS. Glenoid implant orientation and cement failure in total shoulder arthroplasty: a finite element analysis. J Shoulder Elbow Surg. 2013;22(7):940-947. doi:10.1016/j.jse.2012.09.007.
8. Boileau P, Walch G. The three-dimensional geometry of the proximal humerus. Implications for surgical technique and prosthetic design. J Bone Joint Surg Br. 1997;79(5):857-865. doi:10.1302/0301-620X.79B5.0790857.
9. Wu G, van der Helm FC, Veeger HE, et al. ISB recommendation on definitions of joint coordinate systems of various joints for the reporting of human joint motion--Part II: shoulder, elbow, wrist and hand. J Biomech. 2005;38(5):981-992.
10. Kummer FJ, Perkins R, Zuckerman JD. The use of the bicipital groove for alignment of the humeral stem in shoulder arthroplasty. J Shoulder Elbow Surg. 1998;7(2):144-146. doi:10.1016/S1058-2746(98)90225-7.
11. Iannotti JP, Gabriel JP, Schneck SL, Evans BG, Misra S. The normal glenohumeral relationships. An anatomical study of one hundred and forty shoulders. J Bone Joint Surg Am. 1992;74(4):491-500.
12. Pearl ML, Volk AG. Coronal plane geometry of the proximal humerus relevant to prosthetic arthroplasty. J Shoulder Elbow Surg. 1996;5(4):320-326. doi:10.1016/S1058-2746(96)80060-7.
13. Pearl ML. Proximal humeral anatomy in shoulder arthroplasty: Implications for prosthetic design and surgical technique. J Shoulder Elbow Surg. 2005;14(1 Suppl S):99S-104S. doi:10.1016/j.jse.2004.09.025.
14. Prakash U, McGurty DW, Dent JA. Hemiarthroplasty for severe fractures of the proximal humerus. J Shoulder Elbow Surg. 2002;11(5):428-430. doi:10.1067/mse.2002.126615.
15. Robinson CM, Page RS, Hill RM, Sanders DL, Court-Brown CM, Wakefield AE. Primary hemiarthroplasty for treatment of proximal humeral fractures. J Bone Joint Surg Am. 2003;85-A(7):1215-1223.
16. Zyto K, Wallace WA, Frostick SP, Preston BJ. Outcome after hemiarthroplasty for three- and four-part fractures of the proximal humerus. J Shoulder Elbow Surg. 1998;7(2):85-89. doi:10.1016/S1058-2746(98)90215-4.
ABSTRACT
The objective of this study is to determine the reproducibility and feasibility of using 3-dimensional (3-D) computer simulation of proximal humerus fracture computed tomography (CT) scans for fracture reduction. We hypothesized that anatomic reconstruction with 3-D models would be anatomically accurate and reproducible.
Preoperative CT scans of 28 patients with 3- and 4-part (AO classification 11-B1, 11-B2, 11-C1, 11-C2) proximal humerus fractures who were treated by hemiarthroplasty were converted into 3-D computer models. The displaced fractured fragments were anatomically reduced with computer simulation by 2 fellowship-trained shoulder surgeons, and measurements were made of the reconstructed proximal humerus.
The measurements of the reconstructed models had very good to excellent interobserver and intraobserver reliability. The reconstructions of these humerus fractures showed interclass correlation coefficients ranging from 0.71 to 0.93 between 1 observer and from 0.82 to 0.98 between 2 different observers. The fracture reduction was judged against normal proximal humerus geometry to determine reduction accuracy.
The 3-D modeling techniques used to reconstruct 3- and 4-part proximal humerus fractures were reliable and accurate. This technique of modeling and reconstructing proximal humerus fractures could be used to enhance the preoperative planning of open reduction and internal fixation or hemiarthroplasty for 3- and 4-part proximal humerus fractures.
The treatment of proximal humerus fractures is influenced by multiple factors, including patient age, associated injuries, bone quality, and fracture pattern. Three- and 4-part fractures are among the more severe of these fractures, which may result in vascular compromise to the humeral head, leading to avascular necrosis. Surgical goals for the management of these fractures are to optimize functional outcomes by re-creating a stable construct with a functional rotator cuff by open reduction and internal fixation (ORIF), hemiarthroplasty with tuberosity ORIF, or reverse shoulder replacement. Achieving a good outcome following hemiarthroplasty is dependent on many factors, including anatomic tuberosity healing and component positioning.1,2,3 Repairing the greater tuberosity in a near-anatomic position has been shown to greatly affect the results of hemiarthroplasty for fracture.3,4
Continue to: Three-dimensional (3-D) modeling...
Three-dimensional (3-D) modeling is increasingly being used in preoperative planning of shoulder arthroplasty and determining proper proximal humeral fracture treatment. 5 However, no studies have examined the reconstruction of a fractured proximal humerus into native anatomy using computer simulation. The purpose of this study is to determine the accuracy and reliability of anatomically reconstructing the preinjury proximal humerus using 3-D computer models created from postinjury computed tomography (CT) scans. The results of this study could lead to useful techniques employing CT–based models for patient-specific preoperative planning of proximal humeral fracture ORIF and during tuberosity reduction and fixation during hemiarthroplasty for fracture. We hypothesize that it is feasible to reconstruct the original anatomy of the proximal humerus by using 3-D computer modeling of proximal humerus fractures with high reliability based on interobserver and intraobserver review.
METHODS
After Institutional Review Board approval was obtained, we reviewed the medical records of consecutive patients with a diagnosis of proximal humeral fracture and the treatment codes for hemiarthroplasty from 2000 to 2013. Inclusion criteria included 3- and 4-part fractures (AO classifications 11-B1, 11-B2, 11-C1, 11-C2). CT scans with insufficient quality to differentiate bone from soft tissue (inadequate signal-to-noise ratio) were excluded from the study. A total of 28 patients with adequate CT scans met the criteria for inclusion in this study.
The CT scan protocol included 0.5-mm axial cuts with inclusion of the proximal humerus in the Digital Imaging and Communications in Medicine format. These CT scans were converted into patient-specific 3-D computer models of the shoulder using Mimics software (Materialise Inc.). The use of this software to produce anatomically accurate models has previously been verified in a shoulder model.6,7 The tuberosity fragments were then individually separated from each other using the voxel-selecting capabilities of 3-D software and manipulated with translation and rotation for anatomic reduction (Figures 1A-1D, Figure 2).
The de-identified anatomically reconstructed shoulder models were then uploaded into Materialise’s Magics rapid prototyping software, and a user-defined humeral Cartesian coordinate system was defined with anatomic landmarks as reference points to standardize the position of each model (Figure 3).8,9
A series of measurements were made on these models to assess the validity and reliability of the reassembly. The bicipital groove at the anatomic neck was used to measure humeral head version as described by Kummer and colleagues.10 The head-shaft angle, humeral head-greater tuberosity distance, humeral head-bicipital groove angle, and posterior and medial humeral head offset were measured directly on the reconstructed humerus.
Continue to: Two fellowship-trained shoulder...
Two fellowship-trained shoulder surgeons independently reassembled these fracture fragments via computer simulation. Interobserver reliability testing was conducted on these reconstructions by measuring the geometry between the 2 different surgeons’ reconstructions. Intraobserver reliability testing was conducted by 1 surgeon repeating the reconstructions with 4-week intervals between trials and measuring the geometry between the 2 different trials. The average dimensions of the reconstructed proximal humerus fractures were compared with the geometry of normal humeri reported in previously conducted anatomic studies.11,12,13
STATISTICS
The measured dimensions of the 28 reassembled proximal humeri models were averaged across all trials between the 2 fellowship-trained surgeons and compared with the range of normal dimensions of a healthy proximal humerus using the 2 one-sided tests (TOST) method for equivalence between 2 means given a range. The interobserver and intraobserver reliabilities were quantified using the interclass correlation coefficient. An excellent correlation was defined as a correlation coefficient >0.81; very good was defined as 0.61 to 0.80; and good was defined as 0.41 to 0.60.
RESULTS
Of the patients studied, 9 (32.1%) were male, and the average age at the time of CT scanning was 72 years. Of the 28 patients with fracture, 18 (64.2%) had 3-part fractures (AO classifications 11-B1, 11-B2), and 10 (35.8%) had 4-part fractures (AO classifications 11-C1, 11-C2). When examining the location of the intertubercular fracture line, we found that 13 (46.4%) fractures went through the bicipital groove. Of the remaining fracture lines, 9 (32.1%) extended into the greater tuberosity and 6 (21.4%) extended into the lesser tuberosity.
All users were able to reconstruct all 28 fractures using this technique. The average measured dimensions fell within the range of dimensions of a normal healthy proximal humerus specified in the literature to within a 95% confidence interval using the TOST for equivalence, in which we compared measured values with ranges reported in the literature (Table).11,12,13
Table. Dimensions of Proximal Humerus Geometry
| Normal Parameters | Average Dimensions From Trials | Dimensions From Literature |
| Head shaft angle | 43.5° ± 1° | 42.5° ± 12.5° |
| Head to greater tuberosity distance | 4.9 mm ± 0.4 mm | 8 mm ± 3.2 mm |
Head to bicipital groove angle (anatomic neck) | 26.4° ± 2° | 27.3° ± 14° |
| Posterior humeral head offset | 1.6 mm ± 0.3 mm | 4 mm ± 6 mm |
| Medial humeral head offset | 4.5 mm ± 0.3 mm | 9 mm ± 5 mm |
The reconstructions of these humerus fractures showed intraclass correlation coefficients ranging from 0.71 to 0.93 in 1 observer and interclass correlation coefficients from 0.82 to 0.98 between 2 different observers (Table).
DISCUSSION
This study demonstrates that it is feasible to reliably and accurately reconstruct the original anatomy of the proximal humerus by using 3-D computer modeling of proximal humerus fractures. Poor outcomes after hemiarthroplasty for proximal humerus fractures are mostly related to tuberosity malpositioning, resorption, or failure of fixation and resultant dysfunction of the rotator cuff.14,15,16 These studies highlight the importance of accurate tuberosity reduction during surgical care of these fractures.
Continue to: The 3-D computer model...
The 3-D computer model reconstruction of 3- and 4-part proximal humerus fractures were reliable and valid. The interclass correlation coefficients showed very good to excellent interobserver and intraobserver reliability for all measurements conducted. The averaged dimensions from all trials fell within the appropriate range of dimensions for a normal healthy humerus reported in the literature, as verified by the TOST method.11,12,13 The 3-D modeling capabilities demonstrated in this study allowed a greater understanding of the fracture patterns present in 3- and 4-part (AO classifications 11-B1, 11-B2, 11-C1, 11-C2) humerus fractures.
Overreduction of greater tuberosity to create cortical overlap with the lateral shaft may be used to promote bony union. As a result of this distalization, there may be extra strains placed on the rotator cuff, making the patient more prone to rotator cuff tear, as well as improperly balancing the dynamic stabilizers of the shoulder. Poor clinical outcomes in hemiarthroplasty for proximal humerus fractures have been correlated with a greater tuberosity placed distal relative to the humeral head by 1 cm in a study2 and by 2 cm in another.3
This study has several limitations. The first is the assumption that our injured patients had preinjury proximal humerus geometry within the range of normal dimensions of a healthy humerus. Unfortunately, because we were unable to obtain CT scans of the contralateral shoulder, we had to use standard proximal humerus geometry as the control. Another limitation, inherent in the technique, is that only cortical and dense trabecular bone was modeled, so that comminuted or osteoporotic bone was not well modeled. This study did not correlate the findings from these models with clinical outcomes. A prospective study is needed to evaluate the impact of this 3-D modeling on fracture reductions and clinical outcomes.
This study demonstrates that patient-specific modeling of proximal humerus fracture 3-D CT scans may help surgeons reliably and accurately reconstruct fractures. This technique may have utility in the preoperative planning of tuberosity fracture reduction and hemiarthroplasty. It gives surgeons the ability to visualize fracture fragments, and the process of reconstructing the fragments may help surgeons understand the required maneuvers for reduction at the time of surgery. This technique also provides dimensions of the patient’s native humerus, thus potentially improving the anatomic accuracy of the reduction or hemiarthroplasty reconstruction. With the new trend toward patient-specific instrumentation, this study also provides a means of planning the size of the humeral prostheses as well as the version relative to the biceps groove and intertubercular fracture line.
CONCLUSION
This study demonstrates the feasibility of using 3-D computer modeling of complex proximal humerus fractures in anatomic reconstruction. These techniques of computer-simulated 3-D models are valid and reliable. We believe that this technique of modeling and reconstructing proximal humerus fractures could be used to enhance the preoperative planning of hemiarthroplasty for 3- and 4-part proximal humerus fractures by providing improved understanding of the patient’s native humeral geometry and tuberosity reduction.
ABSTRACT
The objective of this study is to determine the reproducibility and feasibility of using 3-dimensional (3-D) computer simulation of proximal humerus fracture computed tomography (CT) scans for fracture reduction. We hypothesized that anatomic reconstruction with 3-D models would be anatomically accurate and reproducible.
Preoperative CT scans of 28 patients with 3- and 4-part (AO classification 11-B1, 11-B2, 11-C1, 11-C2) proximal humerus fractures who were treated by hemiarthroplasty were converted into 3-D computer models. The displaced fractured fragments were anatomically reduced with computer simulation by 2 fellowship-trained shoulder surgeons, and measurements were made of the reconstructed proximal humerus.
The measurements of the reconstructed models had very good to excellent interobserver and intraobserver reliability. The reconstructions of these humerus fractures showed interclass correlation coefficients ranging from 0.71 to 0.93 between 1 observer and from 0.82 to 0.98 between 2 different observers. The fracture reduction was judged against normal proximal humerus geometry to determine reduction accuracy.
The 3-D modeling techniques used to reconstruct 3- and 4-part proximal humerus fractures were reliable and accurate. This technique of modeling and reconstructing proximal humerus fractures could be used to enhance the preoperative planning of open reduction and internal fixation or hemiarthroplasty for 3- and 4-part proximal humerus fractures.
The treatment of proximal humerus fractures is influenced by multiple factors, including patient age, associated injuries, bone quality, and fracture pattern. Three- and 4-part fractures are among the more severe of these fractures, which may result in vascular compromise to the humeral head, leading to avascular necrosis. Surgical goals for the management of these fractures are to optimize functional outcomes by re-creating a stable construct with a functional rotator cuff by open reduction and internal fixation (ORIF), hemiarthroplasty with tuberosity ORIF, or reverse shoulder replacement. Achieving a good outcome following hemiarthroplasty is dependent on many factors, including anatomic tuberosity healing and component positioning.1,2,3 Repairing the greater tuberosity in a near-anatomic position has been shown to greatly affect the results of hemiarthroplasty for fracture.3,4
Continue to: Three-dimensional (3-D) modeling...
Three-dimensional (3-D) modeling is increasingly being used in preoperative planning of shoulder arthroplasty and determining proper proximal humeral fracture treatment. 5 However, no studies have examined the reconstruction of a fractured proximal humerus into native anatomy using computer simulation. The purpose of this study is to determine the accuracy and reliability of anatomically reconstructing the preinjury proximal humerus using 3-D computer models created from postinjury computed tomography (CT) scans. The results of this study could lead to useful techniques employing CT–based models for patient-specific preoperative planning of proximal humeral fracture ORIF and during tuberosity reduction and fixation during hemiarthroplasty for fracture. We hypothesize that it is feasible to reconstruct the original anatomy of the proximal humerus by using 3-D computer modeling of proximal humerus fractures with high reliability based on interobserver and intraobserver review.
METHODS
After Institutional Review Board approval was obtained, we reviewed the medical records of consecutive patients with a diagnosis of proximal humeral fracture and the treatment codes for hemiarthroplasty from 2000 to 2013. Inclusion criteria included 3- and 4-part fractures (AO classifications 11-B1, 11-B2, 11-C1, 11-C2). CT scans with insufficient quality to differentiate bone from soft tissue (inadequate signal-to-noise ratio) were excluded from the study. A total of 28 patients with adequate CT scans met the criteria for inclusion in this study.
The CT scan protocol included 0.5-mm axial cuts with inclusion of the proximal humerus in the Digital Imaging and Communications in Medicine format. These CT scans were converted into patient-specific 3-D computer models of the shoulder using Mimics software (Materialise Inc.). The use of this software to produce anatomically accurate models has previously been verified in a shoulder model.6,7 The tuberosity fragments were then individually separated from each other using the voxel-selecting capabilities of 3-D software and manipulated with translation and rotation for anatomic reduction (Figures 1A-1D, Figure 2).
The de-identified anatomically reconstructed shoulder models were then uploaded into Materialise’s Magics rapid prototyping software, and a user-defined humeral Cartesian coordinate system was defined with anatomic landmarks as reference points to standardize the position of each model (Figure 3).8,9
A series of measurements were made on these models to assess the validity and reliability of the reassembly. The bicipital groove at the anatomic neck was used to measure humeral head version as described by Kummer and colleagues.10 The head-shaft angle, humeral head-greater tuberosity distance, humeral head-bicipital groove angle, and posterior and medial humeral head offset were measured directly on the reconstructed humerus.
Continue to: Two fellowship-trained shoulder...
Two fellowship-trained shoulder surgeons independently reassembled these fracture fragments via computer simulation. Interobserver reliability testing was conducted on these reconstructions by measuring the geometry between the 2 different surgeons’ reconstructions. Intraobserver reliability testing was conducted by 1 surgeon repeating the reconstructions with 4-week intervals between trials and measuring the geometry between the 2 different trials. The average dimensions of the reconstructed proximal humerus fractures were compared with the geometry of normal humeri reported in previously conducted anatomic studies.11,12,13
STATISTICS
The measured dimensions of the 28 reassembled proximal humeri models were averaged across all trials between the 2 fellowship-trained surgeons and compared with the range of normal dimensions of a healthy proximal humerus using the 2 one-sided tests (TOST) method for equivalence between 2 means given a range. The interobserver and intraobserver reliabilities were quantified using the interclass correlation coefficient. An excellent correlation was defined as a correlation coefficient >0.81; very good was defined as 0.61 to 0.80; and good was defined as 0.41 to 0.60.
RESULTS
Of the patients studied, 9 (32.1%) were male, and the average age at the time of CT scanning was 72 years. Of the 28 patients with fracture, 18 (64.2%) had 3-part fractures (AO classifications 11-B1, 11-B2), and 10 (35.8%) had 4-part fractures (AO classifications 11-C1, 11-C2). When examining the location of the intertubercular fracture line, we found that 13 (46.4%) fractures went through the bicipital groove. Of the remaining fracture lines, 9 (32.1%) extended into the greater tuberosity and 6 (21.4%) extended into the lesser tuberosity.
All users were able to reconstruct all 28 fractures using this technique. The average measured dimensions fell within the range of dimensions of a normal healthy proximal humerus specified in the literature to within a 95% confidence interval using the TOST for equivalence, in which we compared measured values with ranges reported in the literature (Table).11,12,13
Table. Dimensions of Proximal Humerus Geometry
| Normal Parameters | Average Dimensions From Trials | Dimensions From Literature |
| Head shaft angle | 43.5° ± 1° | 42.5° ± 12.5° |
| Head to greater tuberosity distance | 4.9 mm ± 0.4 mm | 8 mm ± 3.2 mm |
Head to bicipital groove angle (anatomic neck) | 26.4° ± 2° | 27.3° ± 14° |
| Posterior humeral head offset | 1.6 mm ± 0.3 mm | 4 mm ± 6 mm |
| Medial humeral head offset | 4.5 mm ± 0.3 mm | 9 mm ± 5 mm |
The reconstructions of these humerus fractures showed intraclass correlation coefficients ranging from 0.71 to 0.93 in 1 observer and interclass correlation coefficients from 0.82 to 0.98 between 2 different observers (Table).
DISCUSSION
This study demonstrates that it is feasible to reliably and accurately reconstruct the original anatomy of the proximal humerus by using 3-D computer modeling of proximal humerus fractures. Poor outcomes after hemiarthroplasty for proximal humerus fractures are mostly related to tuberosity malpositioning, resorption, or failure of fixation and resultant dysfunction of the rotator cuff.14,15,16 These studies highlight the importance of accurate tuberosity reduction during surgical care of these fractures.
Continue to: The 3-D computer model...
The 3-D computer model reconstruction of 3- and 4-part proximal humerus fractures were reliable and valid. The interclass correlation coefficients showed very good to excellent interobserver and intraobserver reliability for all measurements conducted. The averaged dimensions from all trials fell within the appropriate range of dimensions for a normal healthy humerus reported in the literature, as verified by the TOST method.11,12,13 The 3-D modeling capabilities demonstrated in this study allowed a greater understanding of the fracture patterns present in 3- and 4-part (AO classifications 11-B1, 11-B2, 11-C1, 11-C2) humerus fractures.
Overreduction of greater tuberosity to create cortical overlap with the lateral shaft may be used to promote bony union. As a result of this distalization, there may be extra strains placed on the rotator cuff, making the patient more prone to rotator cuff tear, as well as improperly balancing the dynamic stabilizers of the shoulder. Poor clinical outcomes in hemiarthroplasty for proximal humerus fractures have been correlated with a greater tuberosity placed distal relative to the humeral head by 1 cm in a study2 and by 2 cm in another.3
This study has several limitations. The first is the assumption that our injured patients had preinjury proximal humerus geometry within the range of normal dimensions of a healthy humerus. Unfortunately, because we were unable to obtain CT scans of the contralateral shoulder, we had to use standard proximal humerus geometry as the control. Another limitation, inherent in the technique, is that only cortical and dense trabecular bone was modeled, so that comminuted or osteoporotic bone was not well modeled. This study did not correlate the findings from these models with clinical outcomes. A prospective study is needed to evaluate the impact of this 3-D modeling on fracture reductions and clinical outcomes.
This study demonstrates that patient-specific modeling of proximal humerus fracture 3-D CT scans may help surgeons reliably and accurately reconstruct fractures. This technique may have utility in the preoperative planning of tuberosity fracture reduction and hemiarthroplasty. It gives surgeons the ability to visualize fracture fragments, and the process of reconstructing the fragments may help surgeons understand the required maneuvers for reduction at the time of surgery. This technique also provides dimensions of the patient’s native humerus, thus potentially improving the anatomic accuracy of the reduction or hemiarthroplasty reconstruction. With the new trend toward patient-specific instrumentation, this study also provides a means of planning the size of the humeral prostheses as well as the version relative to the biceps groove and intertubercular fracture line.
CONCLUSION
This study demonstrates the feasibility of using 3-D computer modeling of complex proximal humerus fractures in anatomic reconstruction. These techniques of computer-simulated 3-D models are valid and reliable. We believe that this technique of modeling and reconstructing proximal humerus fractures could be used to enhance the preoperative planning of hemiarthroplasty for 3- and 4-part proximal humerus fractures by providing improved understanding of the patient’s native humeral geometry and tuberosity reduction.
1. Boileau P, Krishnan SG, Tinsi L, Walch G, Coste JS, Mole D. Tuberosity malposition and migration: reasons for poor outcomes after hemiarthroplasty for displaced fractures of the proximal humerus. J Shoulder Elbow Surg. 2002;11(5):401-412. doi:10.1067/mse.2002.124527.
2. Mighell MA, Kolm GP, Collinge CA, Frankle MA. Outcomes of hemiarthroplasty for fractures of the proximal humerus. J Shoulder Elbow Surg. 2003;12(6):569-577. doi:10.1016/S1058274603002131.
3. Greiner SH, Kaab MJ, Kroning I, Scheibel M, Perka C. Reconstruction of humeral length and centering of the prosthetic head in hemiarthroplasty for proximal humeral fractures. J Shoulder Elbow Surg. 2008;17(5):709-714. doi:10.1016/j.jse.2008.03.004.
4. Smith AM, Mardones RM, Sperling JW, Cofield RH. Early complications of operatively treated proximal humeral fractures. J Shoulder Elbow Surg. 2007;16(1):14-24. doi:10.1016/j.jse.2006.05.008.
5. Scalise JJ, Codsi MJ, Bryan J, Iannotti JP. The three-dimensional glenoid vault model can estimate normal glenoid version in osteoarthritis. J Shoulder Elbow Surg. 2008;17(3):487-491. doi:10.1016/j.jse.2007.09.006.
6. Bryce CD, Pennypacker JL, Kulkarni N, et al. Validation of three-dimensional models of in situ scapulae. J Shoulder Elbow Surg. 2008;17(5):825-832. doi:10.1016/j.jse.2008.01.141.
7. Yongpravat C, Kim HM, Gardner TR, Bigliani LU, Levine WN, Ahmad CS. Glenoid implant orientation and cement failure in total shoulder arthroplasty: a finite element analysis. J Shoulder Elbow Surg. 2013;22(7):940-947. doi:10.1016/j.jse.2012.09.007.
8. Boileau P, Walch G. The three-dimensional geometry of the proximal humerus. Implications for surgical technique and prosthetic design. J Bone Joint Surg Br. 1997;79(5):857-865. doi:10.1302/0301-620X.79B5.0790857.
9. Wu G, van der Helm FC, Veeger HE, et al. ISB recommendation on definitions of joint coordinate systems of various joints for the reporting of human joint motion--Part II: shoulder, elbow, wrist and hand. J Biomech. 2005;38(5):981-992.
10. Kummer FJ, Perkins R, Zuckerman JD. The use of the bicipital groove for alignment of the humeral stem in shoulder arthroplasty. J Shoulder Elbow Surg. 1998;7(2):144-146. doi:10.1016/S1058-2746(98)90225-7.
11. Iannotti JP, Gabriel JP, Schneck SL, Evans BG, Misra S. The normal glenohumeral relationships. An anatomical study of one hundred and forty shoulders. J Bone Joint Surg Am. 1992;74(4):491-500.
12. Pearl ML, Volk AG. Coronal plane geometry of the proximal humerus relevant to prosthetic arthroplasty. J Shoulder Elbow Surg. 1996;5(4):320-326. doi:10.1016/S1058-2746(96)80060-7.
13. Pearl ML. Proximal humeral anatomy in shoulder arthroplasty: Implications for prosthetic design and surgical technique. J Shoulder Elbow Surg. 2005;14(1 Suppl S):99S-104S. doi:10.1016/j.jse.2004.09.025.
14. Prakash U, McGurty DW, Dent JA. Hemiarthroplasty for severe fractures of the proximal humerus. J Shoulder Elbow Surg. 2002;11(5):428-430. doi:10.1067/mse.2002.126615.
15. Robinson CM, Page RS, Hill RM, Sanders DL, Court-Brown CM, Wakefield AE. Primary hemiarthroplasty for treatment of proximal humeral fractures. J Bone Joint Surg Am. 2003;85-A(7):1215-1223.
16. Zyto K, Wallace WA, Frostick SP, Preston BJ. Outcome after hemiarthroplasty for three- and four-part fractures of the proximal humerus. J Shoulder Elbow Surg. 1998;7(2):85-89. doi:10.1016/S1058-2746(98)90215-4.
1. Boileau P, Krishnan SG, Tinsi L, Walch G, Coste JS, Mole D. Tuberosity malposition and migration: reasons for poor outcomes after hemiarthroplasty for displaced fractures of the proximal humerus. J Shoulder Elbow Surg. 2002;11(5):401-412. doi:10.1067/mse.2002.124527.
2. Mighell MA, Kolm GP, Collinge CA, Frankle MA. Outcomes of hemiarthroplasty for fractures of the proximal humerus. J Shoulder Elbow Surg. 2003;12(6):569-577. doi:10.1016/S1058274603002131.
3. Greiner SH, Kaab MJ, Kroning I, Scheibel M, Perka C. Reconstruction of humeral length and centering of the prosthetic head in hemiarthroplasty for proximal humeral fractures. J Shoulder Elbow Surg. 2008;17(5):709-714. doi:10.1016/j.jse.2008.03.004.
4. Smith AM, Mardones RM, Sperling JW, Cofield RH. Early complications of operatively treated proximal humeral fractures. J Shoulder Elbow Surg. 2007;16(1):14-24. doi:10.1016/j.jse.2006.05.008.
5. Scalise JJ, Codsi MJ, Bryan J, Iannotti JP. The three-dimensional glenoid vault model can estimate normal glenoid version in osteoarthritis. J Shoulder Elbow Surg. 2008;17(3):487-491. doi:10.1016/j.jse.2007.09.006.
6. Bryce CD, Pennypacker JL, Kulkarni N, et al. Validation of three-dimensional models of in situ scapulae. J Shoulder Elbow Surg. 2008;17(5):825-832. doi:10.1016/j.jse.2008.01.141.
7. Yongpravat C, Kim HM, Gardner TR, Bigliani LU, Levine WN, Ahmad CS. Glenoid implant orientation and cement failure in total shoulder arthroplasty: a finite element analysis. J Shoulder Elbow Surg. 2013;22(7):940-947. doi:10.1016/j.jse.2012.09.007.
8. Boileau P, Walch G. The three-dimensional geometry of the proximal humerus. Implications for surgical technique and prosthetic design. J Bone Joint Surg Br. 1997;79(5):857-865. doi:10.1302/0301-620X.79B5.0790857.
9. Wu G, van der Helm FC, Veeger HE, et al. ISB recommendation on definitions of joint coordinate systems of various joints for the reporting of human joint motion--Part II: shoulder, elbow, wrist and hand. J Biomech. 2005;38(5):981-992.
10. Kummer FJ, Perkins R, Zuckerman JD. The use of the bicipital groove for alignment of the humeral stem in shoulder arthroplasty. J Shoulder Elbow Surg. 1998;7(2):144-146. doi:10.1016/S1058-2746(98)90225-7.
11. Iannotti JP, Gabriel JP, Schneck SL, Evans BG, Misra S. The normal glenohumeral relationships. An anatomical study of one hundred and forty shoulders. J Bone Joint Surg Am. 1992;74(4):491-500.
12. Pearl ML, Volk AG. Coronal plane geometry of the proximal humerus relevant to prosthetic arthroplasty. J Shoulder Elbow Surg. 1996;5(4):320-326. doi:10.1016/S1058-2746(96)80060-7.
13. Pearl ML. Proximal humeral anatomy in shoulder arthroplasty: Implications for prosthetic design and surgical technique. J Shoulder Elbow Surg. 2005;14(1 Suppl S):99S-104S. doi:10.1016/j.jse.2004.09.025.
14. Prakash U, McGurty DW, Dent JA. Hemiarthroplasty for severe fractures of the proximal humerus. J Shoulder Elbow Surg. 2002;11(5):428-430. doi:10.1067/mse.2002.126615.
15. Robinson CM, Page RS, Hill RM, Sanders DL, Court-Brown CM, Wakefield AE. Primary hemiarthroplasty for treatment of proximal humeral fractures. J Bone Joint Surg Am. 2003;85-A(7):1215-1223.
16. Zyto K, Wallace WA, Frostick SP, Preston BJ. Outcome after hemiarthroplasty for three- and four-part fractures of the proximal humerus. J Shoulder Elbow Surg. 1998;7(2):85-89. doi:10.1016/S1058-2746(98)90215-4.
TAKE-HOME POINTS
- Proximal humerus fractures may be better understood with 3-D CT imaging.
- 3-D computer modeling of complex proximal humerus fractures allows an understanding of tuebroisty reduction durring ORIF or hemiarthroplasty.
- 3-D modeling enhances preoperative planning for hemiarthroplasty implant size and position relative to the repaired tuberosity fragments.
- 3-D modeling of fracture reduction can help surgeons understand the patient’s native humeral geometry and anatomy.
- Preoperative evaluation of fracture characteristics and fragment reduction help surgeons better understand surgical solutions.