User login
Proximal Humerus Fracture 3-D Modeling
ABSTRACT
The objective of this study is to determine the reproducibility and feasibility of using 3-dimensional (3-D) computer simulation of proximal humerus fracture computed tomography (CT) scans for fracture reduction. We hypothesized that anatomic reconstruction with 3-D models would be anatomically accurate and reproducible.
Preoperative CT scans of 28 patients with 3- and 4-part (AO classification 11-B1, 11-B2, 11-C1, 11-C2) proximal humerus fractures who were treated by hemiarthroplasty were converted into 3-D computer models. The displaced fractured fragments were anatomically reduced with computer simulation by 2 fellowship-trained shoulder surgeons, and measurements were made of the reconstructed proximal humerus.
The measurements of the reconstructed models had very good to excellent interobserver and intraobserver reliability. The reconstructions of these humerus fractures showed interclass correlation coefficients ranging from 0.71 to 0.93 between 1 observer and from 0.82 to 0.98 between 2 different observers. The fracture reduction was judged against normal proximal humerus geometry to determine reduction accuracy.
The 3-D modeling techniques used to reconstruct 3- and 4-part proximal humerus fractures were reliable and accurate. This technique of modeling and reconstructing proximal humerus fractures could be used to enhance the preoperative planning of open reduction and internal fixation or hemiarthroplasty for 3- and 4-part proximal humerus fractures.
The treatment of proximal humerus fractures is influenced by multiple factors, including patient age, associated injuries, bone quality, and fracture pattern. Three- and 4-part fractures are among the more severe of these fractures, which may result in vascular compromise to the humeral head, leading to avascular necrosis. Surgical goals for the management of these fractures are to optimize functional outcomes by re-creating a stable construct with a functional rotator cuff by open reduction and internal fixation (ORIF), hemiarthroplasty with tuberosity ORIF, or reverse shoulder replacement. Achieving a good outcome following hemiarthroplasty is dependent on many factors, including anatomic tuberosity healing and component positioning.1,2,3 Repairing the greater tuberosity in a near-anatomic position has been shown to greatly affect the results of hemiarthroplasty for fracture.3,4
Continue to: Three-dimensional (3-D) modeling...
Three-dimensional (3-D) modeling is increasingly being used in preoperative planning of shoulder arthroplasty and determining proper proximal humeral fracture treatment. 5 However, no studies have examined the reconstruction of a fractured proximal humerus into native anatomy using computer simulation. The purpose of this study is to determine the accuracy and reliability of anatomically reconstructing the preinjury proximal humerus using 3-D computer models created from postinjury computed tomography (CT) scans. The results of this study could lead to useful techniques employing CT–based models for patient-specific preoperative planning of proximal humeral fracture ORIF and during tuberosity reduction and fixation during hemiarthroplasty for fracture. We hypothesize that it is feasible to reconstruct the original anatomy of the proximal humerus by using 3-D computer modeling of proximal humerus fractures with high reliability based on interobserver and intraobserver review.
METHODS
After Institutional Review Board approval was obtained, we reviewed the medical records of consecutive patients with a diagnosis of proximal humeral fracture and the treatment codes for hemiarthroplasty from 2000 to 2013. Inclusion criteria included 3- and 4-part fractures (AO classifications 11-B1, 11-B2, 11-C1, 11-C2). CT scans with insufficient quality to differentiate bone from soft tissue (inadequate signal-to-noise ratio) were excluded from the study. A total of 28 patients with adequate CT scans met the criteria for inclusion in this study.
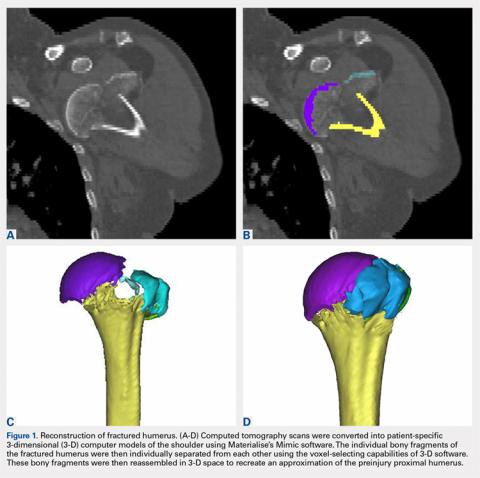
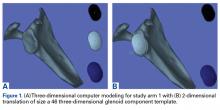
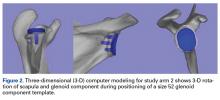
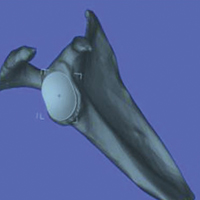
The CT scan protocol included 0.5-mm axial cuts with inclusion of the proximal humerus in the Digital Imaging and Communications in Medicine format. These CT scans were converted into patient-specific 3-D computer models of the shoulder using Mimics software (Materialise Inc.). The use of this software to produce anatomically accurate models has previously been verified in a shoulder model.6,7 The tuberosity fragments were then individually separated from each other using the voxel-selecting capabilities of 3-D software and manipulated with translation and rotation for anatomic reduction (Figures 1A-1D, Figure 2).
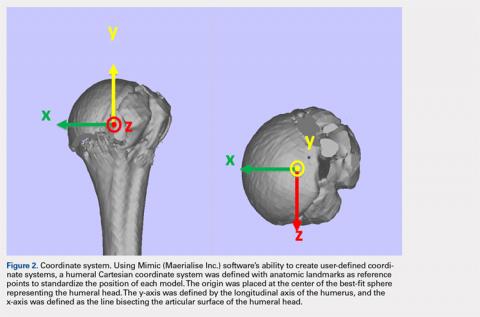
The de-identified anatomically reconstructed shoulder models were then uploaded into Materialise’s Magics rapid prototyping software, and a user-defined humeral Cartesian coordinate system was defined with anatomic landmarks as reference points to standardize the position of each model (Figure 3).8,9
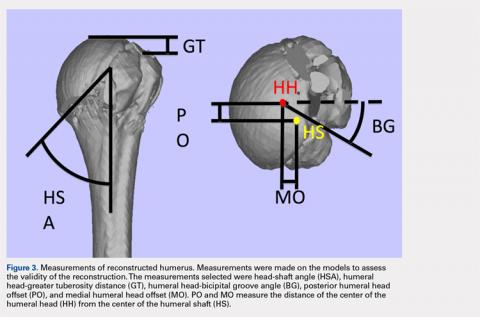
A series of measurements were made on these models to assess the validity and reliability of the reassembly. The bicipital groove at the anatomic neck was used to measure humeral head version as described by Kummer and colleagues.10 The head-shaft angle, humeral head-greater tuberosity distance, humeral head-bicipital groove angle, and posterior and medial humeral head offset were measured directly on the reconstructed humerus.
Continue to: Two fellowship-trained shoulder...
Two fellowship-trained shoulder surgeons independently reassembled these fracture fragments via computer simulation. Interobserver reliability testing was conducted on these reconstructions by measuring the geometry between the 2 different surgeons’ reconstructions. Intraobserver reliability testing was conducted by 1 surgeon repeating the reconstructions with 4-week intervals between trials and measuring the geometry between the 2 different trials. The average dimensions of the reconstructed proximal humerus fractures were compared with the geometry of normal humeri reported in previously conducted anatomic studies.11,12,13
STATISTICS
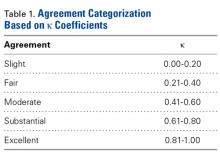
The measured dimensions of the 28 reassembled proximal humeri models were averaged across all trials between the 2 fellowship-trained surgeons and compared with the range of normal dimensions of a healthy proximal humerus using the 2 one-sided tests (TOST) method for equivalence between 2 means given a range. The interobserver and intraobserver reliabilities were quantified using the interclass correlation coefficient. An excellent correlation was defined as a correlation coefficient >0.81; very good was defined as 0.61 to 0.80; and good was defined as 0.41 to 0.60.
RESULTS
Of the patients studied, 9 (32.1%) were male, and the average age at the time of CT scanning was 72 years. Of the 28 patients with fracture, 18 (64.2%) had 3-part fractures (AO classifications 11-B1, 11-B2), and 10 (35.8%) had 4-part fractures (AO classifications 11-C1, 11-C2). When examining the location of the intertubercular fracture line, we found that 13 (46.4%) fractures went through the bicipital groove. Of the remaining fracture lines, 9 (32.1%) extended into the greater tuberosity and 6 (21.4%) extended into the lesser tuberosity.
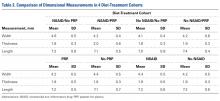
All users were able to reconstruct all 28 fractures using this technique. The average measured dimensions fell within the range of dimensions of a normal healthy proximal humerus specified in the literature to within a 95% confidence interval using the TOST for equivalence, in which we compared measured values with ranges reported in the literature (Table).11,12,13
Table. Dimensions of Proximal Humerus Geometry
| Normal Parameters | Average Dimensions From Trials | Dimensions From Literature |
| Head shaft angle | 43.5° ± 1° | 42.5° ± 12.5° |
| Head to greater tuberosity distance | 4.9 mm ± 0.4 mm | 8 mm ± 3.2 mm |
Head to bicipital groove angle (anatomic neck) | 26.4° ± 2° | 27.3° ± 14° |
| Posterior humeral head offset | 1.6 mm ± 0.3 mm | 4 mm ± 6 mm |
| Medial humeral head offset | 4.5 mm ± 0.3 mm | 9 mm ± 5 mm |
The reconstructions of these humerus fractures showed intraclass correlation coefficients ranging from 0.71 to 0.93 in 1 observer and interclass correlation coefficients from 0.82 to 0.98 between 2 different observers (Table).
DISCUSSION
This study demonstrates that it is feasible to reliably and accurately reconstruct the original anatomy of the proximal humerus by using 3-D computer modeling of proximal humerus fractures. Poor outcomes after hemiarthroplasty for proximal humerus fractures are mostly related to tuberosity malpositioning, resorption, or failure of fixation and resultant dysfunction of the rotator cuff.14,15,16 These studies highlight the importance of accurate tuberosity reduction during surgical care of these fractures.
Continue to: The 3-D computer model...
The 3-D computer model reconstruction of 3- and 4-part proximal humerus fractures were reliable and valid. The interclass correlation coefficients showed very good to excellent interobserver and intraobserver reliability for all measurements conducted. The averaged dimensions from all trials fell within the appropriate range of dimensions for a normal healthy humerus reported in the literature, as verified by the TOST method.11,12,13 The 3-D modeling capabilities demonstrated in this study allowed a greater understanding of the fracture patterns present in 3- and 4-part (AO classifications 11-B1, 11-B2, 11-C1, 11-C2) humerus fractures.
Overreduction of greater tuberosity to create cortical overlap with the lateral shaft may be used to promote bony union. As a result of this distalization, there may be extra strains placed on the rotator cuff, making the patient more prone to rotator cuff tear, as well as improperly balancing the dynamic stabilizers of the shoulder. Poor clinical outcomes in hemiarthroplasty for proximal humerus fractures have been correlated with a greater tuberosity placed distal relative to the humeral head by 1 cm in a study2 and by 2 cm in another.3
This study has several limitations. The first is the assumption that our injured patients had preinjury proximal humerus geometry within the range of normal dimensions of a healthy humerus. Unfortunately, because we were unable to obtain CT scans of the contralateral shoulder, we had to use standard proximal humerus geometry as the control. Another limitation, inherent in the technique, is that only cortical and dense trabecular bone was modeled, so that comminuted or osteoporotic bone was not well modeled. This study did not correlate the findings from these models with clinical outcomes. A prospective study is needed to evaluate the impact of this 3-D modeling on fracture reductions and clinical outcomes.
This study demonstrates that patient-specific modeling of proximal humerus fracture 3-D CT scans may help surgeons reliably and accurately reconstruct fractures. This technique may have utility in the preoperative planning of tuberosity fracture reduction and hemiarthroplasty. It gives surgeons the ability to visualize fracture fragments, and the process of reconstructing the fragments may help surgeons understand the required maneuvers for reduction at the time of surgery. This technique also provides dimensions of the patient’s native humerus, thus potentially improving the anatomic accuracy of the reduction or hemiarthroplasty reconstruction. With the new trend toward patient-specific instrumentation, this study also provides a means of planning the size of the humeral prostheses as well as the version relative to the biceps groove and intertubercular fracture line.
CONCLUSION
This study demonstrates the feasibility of using 3-D computer modeling of complex proximal humerus fractures in anatomic reconstruction. These techniques of computer-simulated 3-D models are valid and reliable. We believe that this technique of modeling and reconstructing proximal humerus fractures could be used to enhance the preoperative planning of hemiarthroplasty for 3- and 4-part proximal humerus fractures by providing improved understanding of the patient’s native humeral geometry and tuberosity reduction.
1. Boileau P, Krishnan SG, Tinsi L, Walch G, Coste JS, Mole D. Tuberosity malposition and migration: reasons for poor outcomes after hemiarthroplasty for displaced fractures of the proximal humerus. J Shoulder Elbow Surg. 2002;11(5):401-412. doi:10.1067/mse.2002.124527.
2. Mighell MA, Kolm GP, Collinge CA, Frankle MA. Outcomes of hemiarthroplasty for fractures of the proximal humerus. J Shoulder Elbow Surg. 2003;12(6):569-577. doi:10.1016/S1058274603002131.
3. Greiner SH, Kaab MJ, Kroning I, Scheibel M, Perka C. Reconstruction of humeral length and centering of the prosthetic head in hemiarthroplasty for proximal humeral fractures. J Shoulder Elbow Surg. 2008;17(5):709-714. doi:10.1016/j.jse.2008.03.004.
4. Smith AM, Mardones RM, Sperling JW, Cofield RH. Early complications of operatively treated proximal humeral fractures. J Shoulder Elbow Surg. 2007;16(1):14-24. doi:10.1016/j.jse.2006.05.008.
5. Scalise JJ, Codsi MJ, Bryan J, Iannotti JP. The three-dimensional glenoid vault model can estimate normal glenoid version in osteoarthritis. J Shoulder Elbow Surg. 2008;17(3):487-491. doi:10.1016/j.jse.2007.09.006.
6. Bryce CD, Pennypacker JL, Kulkarni N, et al. Validation of three-dimensional models of in situ scapulae. J Shoulder Elbow Surg. 2008;17(5):825-832. doi:10.1016/j.jse.2008.01.141.
7. Yongpravat C, Kim HM, Gardner TR, Bigliani LU, Levine WN, Ahmad CS. Glenoid implant orientation and cement failure in total shoulder arthroplasty: a finite element analysis. J Shoulder Elbow Surg. 2013;22(7):940-947. doi:10.1016/j.jse.2012.09.007.
8. Boileau P, Walch G. The three-dimensional geometry of the proximal humerus. Implications for surgical technique and prosthetic design. J Bone Joint Surg Br. 1997;79(5):857-865. doi:10.1302/0301-620X.79B5.0790857.
9. Wu G, van der Helm FC, Veeger HE, et al. ISB recommendation on definitions of joint coordinate systems of various joints for the reporting of human joint motion--Part II: shoulder, elbow, wrist and hand. J Biomech. 2005;38(5):981-992.
10. Kummer FJ, Perkins R, Zuckerman JD. The use of the bicipital groove for alignment of the humeral stem in shoulder arthroplasty. J Shoulder Elbow Surg. 1998;7(2):144-146. doi:10.1016/S1058-2746(98)90225-7.
11. Iannotti JP, Gabriel JP, Schneck SL, Evans BG, Misra S. The normal glenohumeral relationships. An anatomical study of one hundred and forty shoulders. J Bone Joint Surg Am. 1992;74(4):491-500.
12. Pearl ML, Volk AG. Coronal plane geometry of the proximal humerus relevant to prosthetic arthroplasty. J Shoulder Elbow Surg. 1996;5(4):320-326. doi:10.1016/S1058-2746(96)80060-7.
13. Pearl ML. Proximal humeral anatomy in shoulder arthroplasty: Implications for prosthetic design and surgical technique. J Shoulder Elbow Surg. 2005;14(1 Suppl S):99S-104S. doi:10.1016/j.jse.2004.09.025.
14. Prakash U, McGurty DW, Dent JA. Hemiarthroplasty for severe fractures of the proximal humerus. J Shoulder Elbow Surg. 2002;11(5):428-430. doi:10.1067/mse.2002.126615.
15. Robinson CM, Page RS, Hill RM, Sanders DL, Court-Brown CM, Wakefield AE. Primary hemiarthroplasty for treatment of proximal humeral fractures. J Bone Joint Surg Am. 2003;85-A(7):1215-1223.
16. Zyto K, Wallace WA, Frostick SP, Preston BJ. Outcome after hemiarthroplasty for three- and four-part fractures of the proximal humerus. J Shoulder Elbow Surg. 1998;7(2):85-89. doi:10.1016/S1058-2746(98)90215-4.
ABSTRACT
The objective of this study is to determine the reproducibility and feasibility of using 3-dimensional (3-D) computer simulation of proximal humerus fracture computed tomography (CT) scans for fracture reduction. We hypothesized that anatomic reconstruction with 3-D models would be anatomically accurate and reproducible.
Preoperative CT scans of 28 patients with 3- and 4-part (AO classification 11-B1, 11-B2, 11-C1, 11-C2) proximal humerus fractures who were treated by hemiarthroplasty were converted into 3-D computer models. The displaced fractured fragments were anatomically reduced with computer simulation by 2 fellowship-trained shoulder surgeons, and measurements were made of the reconstructed proximal humerus.
The measurements of the reconstructed models had very good to excellent interobserver and intraobserver reliability. The reconstructions of these humerus fractures showed interclass correlation coefficients ranging from 0.71 to 0.93 between 1 observer and from 0.82 to 0.98 between 2 different observers. The fracture reduction was judged against normal proximal humerus geometry to determine reduction accuracy.
The 3-D modeling techniques used to reconstruct 3- and 4-part proximal humerus fractures were reliable and accurate. This technique of modeling and reconstructing proximal humerus fractures could be used to enhance the preoperative planning of open reduction and internal fixation or hemiarthroplasty for 3- and 4-part proximal humerus fractures.
The treatment of proximal humerus fractures is influenced by multiple factors, including patient age, associated injuries, bone quality, and fracture pattern. Three- and 4-part fractures are among the more severe of these fractures, which may result in vascular compromise to the humeral head, leading to avascular necrosis. Surgical goals for the management of these fractures are to optimize functional outcomes by re-creating a stable construct with a functional rotator cuff by open reduction and internal fixation (ORIF), hemiarthroplasty with tuberosity ORIF, or reverse shoulder replacement. Achieving a good outcome following hemiarthroplasty is dependent on many factors, including anatomic tuberosity healing and component positioning.1,2,3 Repairing the greater tuberosity in a near-anatomic position has been shown to greatly affect the results of hemiarthroplasty for fracture.3,4
Continue to: Three-dimensional (3-D) modeling...
Three-dimensional (3-D) modeling is increasingly being used in preoperative planning of shoulder arthroplasty and determining proper proximal humeral fracture treatment. 5 However, no studies have examined the reconstruction of a fractured proximal humerus into native anatomy using computer simulation. The purpose of this study is to determine the accuracy and reliability of anatomically reconstructing the preinjury proximal humerus using 3-D computer models created from postinjury computed tomography (CT) scans. The results of this study could lead to useful techniques employing CT–based models for patient-specific preoperative planning of proximal humeral fracture ORIF and during tuberosity reduction and fixation during hemiarthroplasty for fracture. We hypothesize that it is feasible to reconstruct the original anatomy of the proximal humerus by using 3-D computer modeling of proximal humerus fractures with high reliability based on interobserver and intraobserver review.
METHODS
After Institutional Review Board approval was obtained, we reviewed the medical records of consecutive patients with a diagnosis of proximal humeral fracture and the treatment codes for hemiarthroplasty from 2000 to 2013. Inclusion criteria included 3- and 4-part fractures (AO classifications 11-B1, 11-B2, 11-C1, 11-C2). CT scans with insufficient quality to differentiate bone from soft tissue (inadequate signal-to-noise ratio) were excluded from the study. A total of 28 patients with adequate CT scans met the criteria for inclusion in this study.
The CT scan protocol included 0.5-mm axial cuts with inclusion of the proximal humerus in the Digital Imaging and Communications in Medicine format. These CT scans were converted into patient-specific 3-D computer models of the shoulder using Mimics software (Materialise Inc.). The use of this software to produce anatomically accurate models has previously been verified in a shoulder model.6,7 The tuberosity fragments were then individually separated from each other using the voxel-selecting capabilities of 3-D software and manipulated with translation and rotation for anatomic reduction (Figures 1A-1D, Figure 2).
The de-identified anatomically reconstructed shoulder models were then uploaded into Materialise’s Magics rapid prototyping software, and a user-defined humeral Cartesian coordinate system was defined with anatomic landmarks as reference points to standardize the position of each model (Figure 3).8,9
A series of measurements were made on these models to assess the validity and reliability of the reassembly. The bicipital groove at the anatomic neck was used to measure humeral head version as described by Kummer and colleagues.10 The head-shaft angle, humeral head-greater tuberosity distance, humeral head-bicipital groove angle, and posterior and medial humeral head offset were measured directly on the reconstructed humerus.
Continue to: Two fellowship-trained shoulder...
Two fellowship-trained shoulder surgeons independently reassembled these fracture fragments via computer simulation. Interobserver reliability testing was conducted on these reconstructions by measuring the geometry between the 2 different surgeons’ reconstructions. Intraobserver reliability testing was conducted by 1 surgeon repeating the reconstructions with 4-week intervals between trials and measuring the geometry between the 2 different trials. The average dimensions of the reconstructed proximal humerus fractures were compared with the geometry of normal humeri reported in previously conducted anatomic studies.11,12,13
STATISTICS
The measured dimensions of the 28 reassembled proximal humeri models were averaged across all trials between the 2 fellowship-trained surgeons and compared with the range of normal dimensions of a healthy proximal humerus using the 2 one-sided tests (TOST) method for equivalence between 2 means given a range. The interobserver and intraobserver reliabilities were quantified using the interclass correlation coefficient. An excellent correlation was defined as a correlation coefficient >0.81; very good was defined as 0.61 to 0.80; and good was defined as 0.41 to 0.60.
RESULTS
Of the patients studied, 9 (32.1%) were male, and the average age at the time of CT scanning was 72 years. Of the 28 patients with fracture, 18 (64.2%) had 3-part fractures (AO classifications 11-B1, 11-B2), and 10 (35.8%) had 4-part fractures (AO classifications 11-C1, 11-C2). When examining the location of the intertubercular fracture line, we found that 13 (46.4%) fractures went through the bicipital groove. Of the remaining fracture lines, 9 (32.1%) extended into the greater tuberosity and 6 (21.4%) extended into the lesser tuberosity.
All users were able to reconstruct all 28 fractures using this technique. The average measured dimensions fell within the range of dimensions of a normal healthy proximal humerus specified in the literature to within a 95% confidence interval using the TOST for equivalence, in which we compared measured values with ranges reported in the literature (Table).11,12,13
Table. Dimensions of Proximal Humerus Geometry
| Normal Parameters | Average Dimensions From Trials | Dimensions From Literature |
| Head shaft angle | 43.5° ± 1° | 42.5° ± 12.5° |
| Head to greater tuberosity distance | 4.9 mm ± 0.4 mm | 8 mm ± 3.2 mm |
Head to bicipital groove angle (anatomic neck) | 26.4° ± 2° | 27.3° ± 14° |
| Posterior humeral head offset | 1.6 mm ± 0.3 mm | 4 mm ± 6 mm |
| Medial humeral head offset | 4.5 mm ± 0.3 mm | 9 mm ± 5 mm |
The reconstructions of these humerus fractures showed intraclass correlation coefficients ranging from 0.71 to 0.93 in 1 observer and interclass correlation coefficients from 0.82 to 0.98 between 2 different observers (Table).
DISCUSSION
This study demonstrates that it is feasible to reliably and accurately reconstruct the original anatomy of the proximal humerus by using 3-D computer modeling of proximal humerus fractures. Poor outcomes after hemiarthroplasty for proximal humerus fractures are mostly related to tuberosity malpositioning, resorption, or failure of fixation and resultant dysfunction of the rotator cuff.14,15,16 These studies highlight the importance of accurate tuberosity reduction during surgical care of these fractures.
Continue to: The 3-D computer model...
The 3-D computer model reconstruction of 3- and 4-part proximal humerus fractures were reliable and valid. The interclass correlation coefficients showed very good to excellent interobserver and intraobserver reliability for all measurements conducted. The averaged dimensions from all trials fell within the appropriate range of dimensions for a normal healthy humerus reported in the literature, as verified by the TOST method.11,12,13 The 3-D modeling capabilities demonstrated in this study allowed a greater understanding of the fracture patterns present in 3- and 4-part (AO classifications 11-B1, 11-B2, 11-C1, 11-C2) humerus fractures.
Overreduction of greater tuberosity to create cortical overlap with the lateral shaft may be used to promote bony union. As a result of this distalization, there may be extra strains placed on the rotator cuff, making the patient more prone to rotator cuff tear, as well as improperly balancing the dynamic stabilizers of the shoulder. Poor clinical outcomes in hemiarthroplasty for proximal humerus fractures have been correlated with a greater tuberosity placed distal relative to the humeral head by 1 cm in a study2 and by 2 cm in another.3
This study has several limitations. The first is the assumption that our injured patients had preinjury proximal humerus geometry within the range of normal dimensions of a healthy humerus. Unfortunately, because we were unable to obtain CT scans of the contralateral shoulder, we had to use standard proximal humerus geometry as the control. Another limitation, inherent in the technique, is that only cortical and dense trabecular bone was modeled, so that comminuted or osteoporotic bone was not well modeled. This study did not correlate the findings from these models with clinical outcomes. A prospective study is needed to evaluate the impact of this 3-D modeling on fracture reductions and clinical outcomes.
This study demonstrates that patient-specific modeling of proximal humerus fracture 3-D CT scans may help surgeons reliably and accurately reconstruct fractures. This technique may have utility in the preoperative planning of tuberosity fracture reduction and hemiarthroplasty. It gives surgeons the ability to visualize fracture fragments, and the process of reconstructing the fragments may help surgeons understand the required maneuvers for reduction at the time of surgery. This technique also provides dimensions of the patient’s native humerus, thus potentially improving the anatomic accuracy of the reduction or hemiarthroplasty reconstruction. With the new trend toward patient-specific instrumentation, this study also provides a means of planning the size of the humeral prostheses as well as the version relative to the biceps groove and intertubercular fracture line.
CONCLUSION
This study demonstrates the feasibility of using 3-D computer modeling of complex proximal humerus fractures in anatomic reconstruction. These techniques of computer-simulated 3-D models are valid and reliable. We believe that this technique of modeling and reconstructing proximal humerus fractures could be used to enhance the preoperative planning of hemiarthroplasty for 3- and 4-part proximal humerus fractures by providing improved understanding of the patient’s native humeral geometry and tuberosity reduction.
ABSTRACT
The objective of this study is to determine the reproducibility and feasibility of using 3-dimensional (3-D) computer simulation of proximal humerus fracture computed tomography (CT) scans for fracture reduction. We hypothesized that anatomic reconstruction with 3-D models would be anatomically accurate and reproducible.
Preoperative CT scans of 28 patients with 3- and 4-part (AO classification 11-B1, 11-B2, 11-C1, 11-C2) proximal humerus fractures who were treated by hemiarthroplasty were converted into 3-D computer models. The displaced fractured fragments were anatomically reduced with computer simulation by 2 fellowship-trained shoulder surgeons, and measurements were made of the reconstructed proximal humerus.
The measurements of the reconstructed models had very good to excellent interobserver and intraobserver reliability. The reconstructions of these humerus fractures showed interclass correlation coefficients ranging from 0.71 to 0.93 between 1 observer and from 0.82 to 0.98 between 2 different observers. The fracture reduction was judged against normal proximal humerus geometry to determine reduction accuracy.
The 3-D modeling techniques used to reconstruct 3- and 4-part proximal humerus fractures were reliable and accurate. This technique of modeling and reconstructing proximal humerus fractures could be used to enhance the preoperative planning of open reduction and internal fixation or hemiarthroplasty for 3- and 4-part proximal humerus fractures.
The treatment of proximal humerus fractures is influenced by multiple factors, including patient age, associated injuries, bone quality, and fracture pattern. Three- and 4-part fractures are among the more severe of these fractures, which may result in vascular compromise to the humeral head, leading to avascular necrosis. Surgical goals for the management of these fractures are to optimize functional outcomes by re-creating a stable construct with a functional rotator cuff by open reduction and internal fixation (ORIF), hemiarthroplasty with tuberosity ORIF, or reverse shoulder replacement. Achieving a good outcome following hemiarthroplasty is dependent on many factors, including anatomic tuberosity healing and component positioning.1,2,3 Repairing the greater tuberosity in a near-anatomic position has been shown to greatly affect the results of hemiarthroplasty for fracture.3,4
Continue to: Three-dimensional (3-D) modeling...
Three-dimensional (3-D) modeling is increasingly being used in preoperative planning of shoulder arthroplasty and determining proper proximal humeral fracture treatment. 5 However, no studies have examined the reconstruction of a fractured proximal humerus into native anatomy using computer simulation. The purpose of this study is to determine the accuracy and reliability of anatomically reconstructing the preinjury proximal humerus using 3-D computer models created from postinjury computed tomography (CT) scans. The results of this study could lead to useful techniques employing CT–based models for patient-specific preoperative planning of proximal humeral fracture ORIF and during tuberosity reduction and fixation during hemiarthroplasty for fracture. We hypothesize that it is feasible to reconstruct the original anatomy of the proximal humerus by using 3-D computer modeling of proximal humerus fractures with high reliability based on interobserver and intraobserver review.
METHODS
After Institutional Review Board approval was obtained, we reviewed the medical records of consecutive patients with a diagnosis of proximal humeral fracture and the treatment codes for hemiarthroplasty from 2000 to 2013. Inclusion criteria included 3- and 4-part fractures (AO classifications 11-B1, 11-B2, 11-C1, 11-C2). CT scans with insufficient quality to differentiate bone from soft tissue (inadequate signal-to-noise ratio) were excluded from the study. A total of 28 patients with adequate CT scans met the criteria for inclusion in this study.
The CT scan protocol included 0.5-mm axial cuts with inclusion of the proximal humerus in the Digital Imaging and Communications in Medicine format. These CT scans were converted into patient-specific 3-D computer models of the shoulder using Mimics software (Materialise Inc.). The use of this software to produce anatomically accurate models has previously been verified in a shoulder model.6,7 The tuberosity fragments were then individually separated from each other using the voxel-selecting capabilities of 3-D software and manipulated with translation and rotation for anatomic reduction (Figures 1A-1D, Figure 2).
The de-identified anatomically reconstructed shoulder models were then uploaded into Materialise’s Magics rapid prototyping software, and a user-defined humeral Cartesian coordinate system was defined with anatomic landmarks as reference points to standardize the position of each model (Figure 3).8,9
A series of measurements were made on these models to assess the validity and reliability of the reassembly. The bicipital groove at the anatomic neck was used to measure humeral head version as described by Kummer and colleagues.10 The head-shaft angle, humeral head-greater tuberosity distance, humeral head-bicipital groove angle, and posterior and medial humeral head offset were measured directly on the reconstructed humerus.
Continue to: Two fellowship-trained shoulder...
Two fellowship-trained shoulder surgeons independently reassembled these fracture fragments via computer simulation. Interobserver reliability testing was conducted on these reconstructions by measuring the geometry between the 2 different surgeons’ reconstructions. Intraobserver reliability testing was conducted by 1 surgeon repeating the reconstructions with 4-week intervals between trials and measuring the geometry between the 2 different trials. The average dimensions of the reconstructed proximal humerus fractures were compared with the geometry of normal humeri reported in previously conducted anatomic studies.11,12,13
STATISTICS
The measured dimensions of the 28 reassembled proximal humeri models were averaged across all trials between the 2 fellowship-trained surgeons and compared with the range of normal dimensions of a healthy proximal humerus using the 2 one-sided tests (TOST) method for equivalence between 2 means given a range. The interobserver and intraobserver reliabilities were quantified using the interclass correlation coefficient. An excellent correlation was defined as a correlation coefficient >0.81; very good was defined as 0.61 to 0.80; and good was defined as 0.41 to 0.60.
RESULTS
Of the patients studied, 9 (32.1%) were male, and the average age at the time of CT scanning was 72 years. Of the 28 patients with fracture, 18 (64.2%) had 3-part fractures (AO classifications 11-B1, 11-B2), and 10 (35.8%) had 4-part fractures (AO classifications 11-C1, 11-C2). When examining the location of the intertubercular fracture line, we found that 13 (46.4%) fractures went through the bicipital groove. Of the remaining fracture lines, 9 (32.1%) extended into the greater tuberosity and 6 (21.4%) extended into the lesser tuberosity.
All users were able to reconstruct all 28 fractures using this technique. The average measured dimensions fell within the range of dimensions of a normal healthy proximal humerus specified in the literature to within a 95% confidence interval using the TOST for equivalence, in which we compared measured values with ranges reported in the literature (Table).11,12,13
Table. Dimensions of Proximal Humerus Geometry
| Normal Parameters | Average Dimensions From Trials | Dimensions From Literature |
| Head shaft angle | 43.5° ± 1° | 42.5° ± 12.5° |
| Head to greater tuberosity distance | 4.9 mm ± 0.4 mm | 8 mm ± 3.2 mm |
Head to bicipital groove angle (anatomic neck) | 26.4° ± 2° | 27.3° ± 14° |
| Posterior humeral head offset | 1.6 mm ± 0.3 mm | 4 mm ± 6 mm |
| Medial humeral head offset | 4.5 mm ± 0.3 mm | 9 mm ± 5 mm |
The reconstructions of these humerus fractures showed intraclass correlation coefficients ranging from 0.71 to 0.93 in 1 observer and interclass correlation coefficients from 0.82 to 0.98 between 2 different observers (Table).
DISCUSSION
This study demonstrates that it is feasible to reliably and accurately reconstruct the original anatomy of the proximal humerus by using 3-D computer modeling of proximal humerus fractures. Poor outcomes after hemiarthroplasty for proximal humerus fractures are mostly related to tuberosity malpositioning, resorption, or failure of fixation and resultant dysfunction of the rotator cuff.14,15,16 These studies highlight the importance of accurate tuberosity reduction during surgical care of these fractures.
Continue to: The 3-D computer model...
The 3-D computer model reconstruction of 3- and 4-part proximal humerus fractures were reliable and valid. The interclass correlation coefficients showed very good to excellent interobserver and intraobserver reliability for all measurements conducted. The averaged dimensions from all trials fell within the appropriate range of dimensions for a normal healthy humerus reported in the literature, as verified by the TOST method.11,12,13 The 3-D modeling capabilities demonstrated in this study allowed a greater understanding of the fracture patterns present in 3- and 4-part (AO classifications 11-B1, 11-B2, 11-C1, 11-C2) humerus fractures.
Overreduction of greater tuberosity to create cortical overlap with the lateral shaft may be used to promote bony union. As a result of this distalization, there may be extra strains placed on the rotator cuff, making the patient more prone to rotator cuff tear, as well as improperly balancing the dynamic stabilizers of the shoulder. Poor clinical outcomes in hemiarthroplasty for proximal humerus fractures have been correlated with a greater tuberosity placed distal relative to the humeral head by 1 cm in a study2 and by 2 cm in another.3
This study has several limitations. The first is the assumption that our injured patients had preinjury proximal humerus geometry within the range of normal dimensions of a healthy humerus. Unfortunately, because we were unable to obtain CT scans of the contralateral shoulder, we had to use standard proximal humerus geometry as the control. Another limitation, inherent in the technique, is that only cortical and dense trabecular bone was modeled, so that comminuted or osteoporotic bone was not well modeled. This study did not correlate the findings from these models with clinical outcomes. A prospective study is needed to evaluate the impact of this 3-D modeling on fracture reductions and clinical outcomes.
This study demonstrates that patient-specific modeling of proximal humerus fracture 3-D CT scans may help surgeons reliably and accurately reconstruct fractures. This technique may have utility in the preoperative planning of tuberosity fracture reduction and hemiarthroplasty. It gives surgeons the ability to visualize fracture fragments, and the process of reconstructing the fragments may help surgeons understand the required maneuvers for reduction at the time of surgery. This technique also provides dimensions of the patient’s native humerus, thus potentially improving the anatomic accuracy of the reduction or hemiarthroplasty reconstruction. With the new trend toward patient-specific instrumentation, this study also provides a means of planning the size of the humeral prostheses as well as the version relative to the biceps groove and intertubercular fracture line.
CONCLUSION
This study demonstrates the feasibility of using 3-D computer modeling of complex proximal humerus fractures in anatomic reconstruction. These techniques of computer-simulated 3-D models are valid and reliable. We believe that this technique of modeling and reconstructing proximal humerus fractures could be used to enhance the preoperative planning of hemiarthroplasty for 3- and 4-part proximal humerus fractures by providing improved understanding of the patient’s native humeral geometry and tuberosity reduction.
1. Boileau P, Krishnan SG, Tinsi L, Walch G, Coste JS, Mole D. Tuberosity malposition and migration: reasons for poor outcomes after hemiarthroplasty for displaced fractures of the proximal humerus. J Shoulder Elbow Surg. 2002;11(5):401-412. doi:10.1067/mse.2002.124527.
2. Mighell MA, Kolm GP, Collinge CA, Frankle MA. Outcomes of hemiarthroplasty for fractures of the proximal humerus. J Shoulder Elbow Surg. 2003;12(6):569-577. doi:10.1016/S1058274603002131.
3. Greiner SH, Kaab MJ, Kroning I, Scheibel M, Perka C. Reconstruction of humeral length and centering of the prosthetic head in hemiarthroplasty for proximal humeral fractures. J Shoulder Elbow Surg. 2008;17(5):709-714. doi:10.1016/j.jse.2008.03.004.
4. Smith AM, Mardones RM, Sperling JW, Cofield RH. Early complications of operatively treated proximal humeral fractures. J Shoulder Elbow Surg. 2007;16(1):14-24. doi:10.1016/j.jse.2006.05.008.
5. Scalise JJ, Codsi MJ, Bryan J, Iannotti JP. The three-dimensional glenoid vault model can estimate normal glenoid version in osteoarthritis. J Shoulder Elbow Surg. 2008;17(3):487-491. doi:10.1016/j.jse.2007.09.006.
6. Bryce CD, Pennypacker JL, Kulkarni N, et al. Validation of three-dimensional models of in situ scapulae. J Shoulder Elbow Surg. 2008;17(5):825-832. doi:10.1016/j.jse.2008.01.141.
7. Yongpravat C, Kim HM, Gardner TR, Bigliani LU, Levine WN, Ahmad CS. Glenoid implant orientation and cement failure in total shoulder arthroplasty: a finite element analysis. J Shoulder Elbow Surg. 2013;22(7):940-947. doi:10.1016/j.jse.2012.09.007.
8. Boileau P, Walch G. The three-dimensional geometry of the proximal humerus. Implications for surgical technique and prosthetic design. J Bone Joint Surg Br. 1997;79(5):857-865. doi:10.1302/0301-620X.79B5.0790857.
9. Wu G, van der Helm FC, Veeger HE, et al. ISB recommendation on definitions of joint coordinate systems of various joints for the reporting of human joint motion--Part II: shoulder, elbow, wrist and hand. J Biomech. 2005;38(5):981-992.
10. Kummer FJ, Perkins R, Zuckerman JD. The use of the bicipital groove for alignment of the humeral stem in shoulder arthroplasty. J Shoulder Elbow Surg. 1998;7(2):144-146. doi:10.1016/S1058-2746(98)90225-7.
11. Iannotti JP, Gabriel JP, Schneck SL, Evans BG, Misra S. The normal glenohumeral relationships. An anatomical study of one hundred and forty shoulders. J Bone Joint Surg Am. 1992;74(4):491-500.
12. Pearl ML, Volk AG. Coronal plane geometry of the proximal humerus relevant to prosthetic arthroplasty. J Shoulder Elbow Surg. 1996;5(4):320-326. doi:10.1016/S1058-2746(96)80060-7.
13. Pearl ML. Proximal humeral anatomy in shoulder arthroplasty: Implications for prosthetic design and surgical technique. J Shoulder Elbow Surg. 2005;14(1 Suppl S):99S-104S. doi:10.1016/j.jse.2004.09.025.
14. Prakash U, McGurty DW, Dent JA. Hemiarthroplasty for severe fractures of the proximal humerus. J Shoulder Elbow Surg. 2002;11(5):428-430. doi:10.1067/mse.2002.126615.
15. Robinson CM, Page RS, Hill RM, Sanders DL, Court-Brown CM, Wakefield AE. Primary hemiarthroplasty for treatment of proximal humeral fractures. J Bone Joint Surg Am. 2003;85-A(7):1215-1223.
16. Zyto K, Wallace WA, Frostick SP, Preston BJ. Outcome after hemiarthroplasty for three- and four-part fractures of the proximal humerus. J Shoulder Elbow Surg. 1998;7(2):85-89. doi:10.1016/S1058-2746(98)90215-4.
1. Boileau P, Krishnan SG, Tinsi L, Walch G, Coste JS, Mole D. Tuberosity malposition and migration: reasons for poor outcomes after hemiarthroplasty for displaced fractures of the proximal humerus. J Shoulder Elbow Surg. 2002;11(5):401-412. doi:10.1067/mse.2002.124527.
2. Mighell MA, Kolm GP, Collinge CA, Frankle MA. Outcomes of hemiarthroplasty for fractures of the proximal humerus. J Shoulder Elbow Surg. 2003;12(6):569-577. doi:10.1016/S1058274603002131.
3. Greiner SH, Kaab MJ, Kroning I, Scheibel M, Perka C. Reconstruction of humeral length and centering of the prosthetic head in hemiarthroplasty for proximal humeral fractures. J Shoulder Elbow Surg. 2008;17(5):709-714. doi:10.1016/j.jse.2008.03.004.
4. Smith AM, Mardones RM, Sperling JW, Cofield RH. Early complications of operatively treated proximal humeral fractures. J Shoulder Elbow Surg. 2007;16(1):14-24. doi:10.1016/j.jse.2006.05.008.
5. Scalise JJ, Codsi MJ, Bryan J, Iannotti JP. The three-dimensional glenoid vault model can estimate normal glenoid version in osteoarthritis. J Shoulder Elbow Surg. 2008;17(3):487-491. doi:10.1016/j.jse.2007.09.006.
6. Bryce CD, Pennypacker JL, Kulkarni N, et al. Validation of three-dimensional models of in situ scapulae. J Shoulder Elbow Surg. 2008;17(5):825-832. doi:10.1016/j.jse.2008.01.141.
7. Yongpravat C, Kim HM, Gardner TR, Bigliani LU, Levine WN, Ahmad CS. Glenoid implant orientation and cement failure in total shoulder arthroplasty: a finite element analysis. J Shoulder Elbow Surg. 2013;22(7):940-947. doi:10.1016/j.jse.2012.09.007.
8. Boileau P, Walch G. The three-dimensional geometry of the proximal humerus. Implications for surgical technique and prosthetic design. J Bone Joint Surg Br. 1997;79(5):857-865. doi:10.1302/0301-620X.79B5.0790857.
9. Wu G, van der Helm FC, Veeger HE, et al. ISB recommendation on definitions of joint coordinate systems of various joints for the reporting of human joint motion--Part II: shoulder, elbow, wrist and hand. J Biomech. 2005;38(5):981-992.
10. Kummer FJ, Perkins R, Zuckerman JD. The use of the bicipital groove for alignment of the humeral stem in shoulder arthroplasty. J Shoulder Elbow Surg. 1998;7(2):144-146. doi:10.1016/S1058-2746(98)90225-7.
11. Iannotti JP, Gabriel JP, Schneck SL, Evans BG, Misra S. The normal glenohumeral relationships. An anatomical study of one hundred and forty shoulders. J Bone Joint Surg Am. 1992;74(4):491-500.
12. Pearl ML, Volk AG. Coronal plane geometry of the proximal humerus relevant to prosthetic arthroplasty. J Shoulder Elbow Surg. 1996;5(4):320-326. doi:10.1016/S1058-2746(96)80060-7.
13. Pearl ML. Proximal humeral anatomy in shoulder arthroplasty: Implications for prosthetic design and surgical technique. J Shoulder Elbow Surg. 2005;14(1 Suppl S):99S-104S. doi:10.1016/j.jse.2004.09.025.
14. Prakash U, McGurty DW, Dent JA. Hemiarthroplasty for severe fractures of the proximal humerus. J Shoulder Elbow Surg. 2002;11(5):428-430. doi:10.1067/mse.2002.126615.
15. Robinson CM, Page RS, Hill RM, Sanders DL, Court-Brown CM, Wakefield AE. Primary hemiarthroplasty for treatment of proximal humeral fractures. J Bone Joint Surg Am. 2003;85-A(7):1215-1223.
16. Zyto K, Wallace WA, Frostick SP, Preston BJ. Outcome after hemiarthroplasty for three- and four-part fractures of the proximal humerus. J Shoulder Elbow Surg. 1998;7(2):85-89. doi:10.1016/S1058-2746(98)90215-4.
TAKE-HOME POINTS
- Proximal humerus fractures may be better understood with 3-D CT imaging.
- 3-D computer modeling of complex proximal humerus fractures allows an understanding of tuebroisty reduction durring ORIF or hemiarthroplasty.
- 3-D modeling enhances preoperative planning for hemiarthroplasty implant size and position relative to the repaired tuberosity fragments.
- 3-D modeling of fracture reduction can help surgeons understand the patient’s native humeral geometry and anatomy.
- Preoperative evaluation of fracture characteristics and fragment reduction help surgeons better understand surgical solutions.
Effects of Platelet-Rich Plasma and Indomethacin on Biomechanics of Rotator Cuff Repair
Take-Home Points
- The optimal centrifugation protocol for production of rat PRP is 1300 rpm for 5 minutes.
- PRP administration in RCR improves tendon biomechanics in a rat model.
- Administration of NSAIDs following RCR has no significant effect on tendon biomechanical properties.
- NSAIDs may be co-administered with PRP without reducing efficacy of PRP.
- The role of PRP and NSAIDs in human RCR remains unclear.
Rotator cuff tears are a common source of shoulder pain and disability among older adults and athletes. Full-thickness tears alone occur in up to 30% of adults older than 60 years.1 Surgical repair is plagued by an unpredictable rate of recurrence (range, 11%-94%).1-10 As a result of improved suture materials, knotting patterns, and anchor designs, hardware issues are no longer the primary cause of rotator cuff repair (RCR) failures; now the principal mode of failure is biologic.2 Animal model studies have found that, after injury and subsequent healing, the tendon–bone interface remains abnormal.11 Rotator cuff research therefore has focused largely on biological enhancement of tendon-to-bone healing.
One means of biological augmentation is autologous platelet-rich plasma (PRP), which has supraphysiologic concentrations of platelets and their secreted growth factors. Although there is no consensus on the long-term efficacy of PRP, some studies suggest PRP accelerates healing over short and intermediate terms, which may contribute to a more rapid decrease in pain and more rapid return to normal activities.12-18 Similarly, systemic nonsteroidal anti-inflammatory drugs (NSAIDs) have long been used to treat musculoskeletal injuries, including rotator cuff pathology. However, NSAIDs inhibit cyclooxygenase activity, and clinical and experimental data have shown that cyclooxygenase 2 function is crucial in normal tendon-to-bone healing.19-21
Comprehensive studies have been conducted on the efficacy of both PRP and NSAIDs, but the interaction of concurrently used PRP and NSAIDs has not been determined. As many physicians use both modalities in the treatment of soft-tissue injuries, it is important to study the potential interactions when coadministered. Prior studies in small animal models suggest NSAIDs may impair tendon-to-bone healing in RCR, but there is no evidence regarding the effect of NSAIDs on the efficacy of PRP treatment.21
We conducted a study to determine the interaction of PRP and NSAIDs when used as adjuncts to RCR in a rat model. We hypothesized that PRP would increase the strength of RCR and that NSAIDs would interfere with the effects of PRP. A preliminary study objective was to determine an appropriate centrifugation protocol for producing PRP from rat blood, for use in this study and in future rat-based studies of PRP.
Materials and Methods
Part A: Pretesting Determination of PRP Centrifugation Protocol
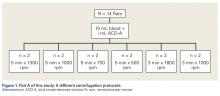
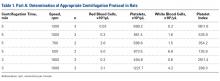
Fourteen adult male Fischer rats were used in part A of this study, which was conducted to determine an appropriate PRP centrifugation protocol. Traditional PRP centrifugation protocols are established for human blood, but rat red blood cells (RBCs) and human RBCs differ in size.22 In our preliminary study, we wanted to determine the adjusted centrifuge speed and duration for producing clinically optimal PRP from rats. Clinically optimal PRP has reduced levels of RBCs, which decrease platelet affinity. Although the role of leukocytes in PRP preparations is debated, reducing the number of white blood cells (WBCs) decreases the number of matrix metalloproteinases and reactive oxygen species that may lead to inflammation. We used the platelet index (ratio of platelets to WBCs) and the RBC count to quantify the quality of our PRP sample.
Each rat in part A was anesthetized while supine. We used the Autologous Conditioned Plasma (ACP) system (Arthrex), which requires only 1 centrifugation cycle to create PRP. About 9 mL or 10 mL of blood was obtained by cardiac aspiration using an ACP Double Syringe (Arthrex). After blood retrieval, a thoracotomy was performed to confirm each rat’s death.
Part B: Determining the Effects of PRP and NSAIDs on RCR in a Rat Model
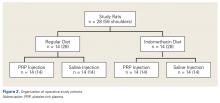
Operative Cohort. Of the 34 Fischer rats used in part B of this study, 6 were used as blood donors for PRP production, and the other 28 underwent bilateral rotator cuff surgeries. We used donor rats to maximize the amount of PRP retrieval, allocating about 1 donor rat per 5 operative rats. Fischer rats are an inbred strain, so the PRP from a donor Fischer rat simulates autologous blood in other Fischer rats. Use of allogenic blood is consistent with prior rat PRP studies.23,24
Operative Technique. Each bilateral surgery was performed by a single board-certified shoulder surgeon, and the anesthetic and surgical protocols were followed as approved by the home institution’s Institutional Animal Care and Use Committee. Before surgery, blood was harvested for PRP production from donor rats, as described earlier, and centrifuged for 5 minutes × 1300 rpm. After anesthetic induction and skin incision, the deltoid muscle was cut to expose the acromion and underlying rotator cuff. The distal supraspinatus tendon was sharply detached from the greater tuberosity. A bone-tunnel RCR was performed by drilling a transverse tunnel across the greater tuberosity and affixing the tendon to its footprint with a 5-0 polypropylene suture (Prolene; Ethicon). Each rat was then randomly assigned to receive 50 µL of donor PRP injected in 1 operative shoulder and saline in the contralateral shoulder. Injections were made in the supraspinatus tendon at its attachment to the humerus. Deltoid and skin were closed with 4-0 polyglactin (Vicryl) suture (Ethicon) and staples, respectively.
Tendon Preparation. Immediately post mortem, each shoulder was grossly dissected to isolate the supraspinatus muscle attached to the humerus. Shoulders were then frozen in 0.15-M saline solution until specified biomechanical testing dates.
On day of dimensional/biomechanical testing, each specimen was thawed at room temperature and finely dissected under a microscope (Stemi 200-C; Car Zeiss). After dissection, the humeral shaft was embedded in polymethylmethacrylate within a test tube. The free end of the supraspinatus tendon was glued within a “tab” of waterproofed emery cloth, leaving about 2 mm of tendon between the tab and the greater tuberosity.
Biomechanical Analysis. A 5848 MicroTester (Instron) was used for biomechanical testing. Each tabbed tendon, held by a pneumatic clamp attached to the MicroTester, was tested in a preconditioning phase and then a ramp-to-failure phase. A constant drip of 0.15-M saline was run through the apparatus to simulate physiologic hydration of tissue. After the embedded specimen was secure within the loading apparatus, an initial tensile preload of 0.2 N was applied. After preloading, the tendon was run through a preconditioning phase to account for viscoelastic relaxation. Immediately after preconditioning, each tendon was subjected to failure testing at a ramp rate of 0.1 mm/s. Force data were collected as a function of displacement, allowing for the calculation of 4 biomechanical parameters: failure force, tendon stiffness and normalized stiffness, energy to failure, and total energy. Tendon stiffness is the slope of a curve-fit line of the initial peak; failure force is the force of the highest peak; energy to failure is the area under the curve (AUC) to the highest peak; and total energy is the AUC from the start of failure ramping to the point at which the tendon is torn off completely. Two-way ANOVA was used to assess the differences between treatment groups and diet groups for all parameters. Statistical significance was set at P < .05.
A power analysis was performed to determine ability to detect differences between cohorts. For power of 80% and P = .05, a difference of 16% of the mean could be detected for failure force, 30% for energy to failure, 14% for total energy to failure, and 24% for stiffness. In addition, a difference of 4% of the mean could be detected for tendon length, 6% for width, and 10% for thickness.
Results
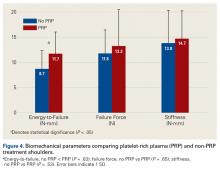
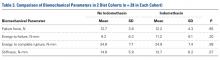
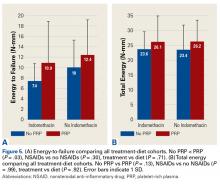
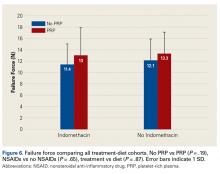
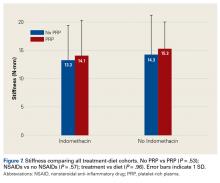
Across all collective treatment-diet groups and biomechanical parameters, there was only 1 statistically significant difference. Mean (SD) energy to failure was significantly higher (P = .03) in shoulders treated with PRP, 11.7 (7.3) N-mm, than in those treated without PRP, 8.7 (4.6) N-mm (Figure 4). There were no statistically significant differences between shoulders treated with indomethacin and those treated without indomethacin (Table 3), and no statistically significant relationships between treatment and drug for any other biomechanical parameter (Figures 5-7).
Discussion
Our preliminary objective in this study was to determine the optimal centrifugation protocol for producing rat-based PRP. Optimal PRP requires a dense concentration of platelets as well as reduced levels of RBCs and WBCs.25 We used the platelet index to quantify the quality of our PRP samples, and we obtained the highest platelet index for the protocol of 5 minutes × 1300 rpm. This finding may be useful in later rat studies involving PRP.
The primary objective of this study was to assess the effect of the interaction of PRP and NSAIDs on RCR. PRP has been found to augment RCR,12,26,27 but indomethacin may impair healing.21,25 We hypothesized that shoulders treated with PRP would have more biomechanical strength than control shoulders and that indomethacin would decrease biomechanical strength.
Our data showed increased energy to failure of the rotator cuff with PRP injections (P = .03). All other biomechanical parameters showed no significant differences with PRP treatment, though there were statistically insignificant trends of increased total energy, failure force, and stiffness in the PRP cohorts. There were no statistically significant differences between the indomethacin and no-indomethacin groups, and indomethacin had no effect on the efficacy of PRP treatment. It should be noted that the measurements of total energy, energy to failure, and failure force best reflect the strength of the tendon–bone interface. Other biomechanical measures, such as stiffness and normalized stiffness, are physical properties of the tendon itself and apply less to enthesis strength, which was the primary focus of this study.
Beck and colleagues23 studied the effect of allogeneic PRP on RCR in a rat model. They tested biomechanical and histologic outcomes 7, 14, and 21 days after surgery. There was no significant difference in failure load between the 2 groups at any time point. Compared with failure strain in the control group, failure strain in the PRP group was decreased at 7 days, normalized at 14 days, and increased at 21 days. The authors hypothesized that increased tendon failure strain at 21 days may have reduced forces being transmitted to the suture fixation site, which may be clinically significant and warrants further investigation. In a similar study, by Dolkart and colleagues,28 intraoperative PRP administration enhanced the maximal load-to-failure and stiffness of rats’ repaired rotator cuffs. On histologic examination, tendons treated with PRP (vs control tendons) had more organized collagen. Although these studies have limitations similar to our study, these results further support improved tendon-to-bone healing with PRP.
In clinical application, Barber and colleagues26 found that, compared with controls, suturing PRP fibrin matrix into the rotator cuff during repair decreased the incidence of magnetic resonance imaging–detected retears. However, in 2 prospective, randomized trials, Castricini and colleagues29 and Weber and colleagues30 found that use of PRP in RCR did not improve outcomes. All 3 studies differ from ours in that they used fibrin matrix. However, Ersen and colleagues31 found no difference in the effects of PRP on rotator cuff healing between injection and fibrin matrix; PRP improved biomechanical properties of repaired rotator cuff independent of administration method. In a meta-analysis of PRP supplementation in RCR, Warth and colleagues32 found a statistically significant improvement in retear rates for tears >3 cm repaired with a double-row technique, but otherwise no overall improvement in retear rates or outcome scores with PRP. The authors acknowledged that the significant heterogeneity of the studies in their meta-analysis may have affected the quality of their data.
Although our study provides some insight into the effectiveness of PRP in tendon repair, the lack of standardization in PRP preparation and time points tested makes comparisons with similar studies difficult.33 Recent reports have emphasized that not all PRP separation systems yield similar products.33 Platelet concentrations, and therefore platelet-derived growth factor concentrations, differ between systems and may yield different clinical outcomes. Our decision to use leukocyte-reduced PRP is supported by a meta-analysis by Riboh and colleagues,34 who reviewed the literature on the effect of leukocyte concentration on the efficacy of PRP products. They found that, in the treatment of knee osteoarthritis, use of leukocyte-poor PRP resulted in improved functional outcomes scores in comparison with placebo, but this improvement did not occur with leukocyte-rich PRP. However, there is still no consensus on optimal preparation, dosing, and route of administration of PRP, and preparations described in the literature vary.
This study also assessed the interaction of PRP and NSAIDs. Although there were no statistically significant differences between treatment and diet, shoulders treated with indomethacin alone showed a trend toward weaker biomechanical parameters in comparison with shoulders treated with saline alone, with PRP alone, or with both PRP and indomethacin. A larger sample would be needed to establish statistical significance. These trends are not surprising, as Cohen and colleagues21 found that NSAIDs, specifically indomethacin and celecoxib, significantly inhibited rotator cuff tendon-to-bone healing. The authors also found that a 2-week course of indomethacin was sufficient to significantly inhibit tendon-to-bone healing. In fact, although the drugs were discontinued after 14 days, biomechanical properties were negatively affected up to 8 weeks after repair. Our results differ from theirs even though the 2 studies used similar doses and administration protocols.
One strength of this study was that all surgeries were performed by a single board-certified surgeon using a standardized technique. In addition, a control group was established, and personnel and techniques for all fine dissections and biomechanical tests were consistent throughout. Blinded randomization and diet normalization, as well as adequate power for detecting significant effects, strengthened the study as well.
The study had several limitations. First, whereas most human rotator cuff tears are chronic, we used a model of acute injury and repair. As acute tears that are immediately repaired are more likely to heal, detection of differences between cohorts is less likely. However, using an acute model is still the most reliable strategy for inducing a controlled injury with reproducible severity. Second, we analyzed data at only 1 time point, which may not provide an accurate representation of long-term effects. Third, systemic administration of indomethacin did not allow for intra-rat shoulder comparisons of the different drug groups. Fourth, although it is possible that the dosage of NSAID was insufficient to produce significant differences in biomechanics, our dosage was consistent with that used in a study that found a significant effect on tendon healing.21
Conclusion
Our study found that the strength of the supraspinatus tendon enthesis as defined by energy to failure was increased with intratendinous PRP injection. Indomethacin showed no statistical effect, but there was a trend toward reduced strength after repair. However, the extent to which coadministration of indomethacin affects PRP remains unclear, and these data cannot necessarily be extrapolated to the typical human rotator cuff tear caused by chronic repetitive stress.
1. Kinsella KG, Velkoff VA. An Aging World: 2001. Washington, DC: US Government Printing Office; 2001. https://www.census.gov/prod/2001pubs/p95-01-1.pdf. Published November 2001. Accessed September 24, 2017.
2. Gamradt SC, Rodeo SA, Warren RF. Platelet rich plasma in rotator cuff repair. Tech Orthop. 2007;22(1):26-33.
3. Galatz LM, Ball CM, Teefey SA, Middleton WD, Yamaguchi K. The outcome and repair integrity of completely arthroscopically repaired large and massive rotator cuff tears. J Bone Joint Surg Am. 2004;86(2):219-224.
4. Harryman DT, Mack LA, Wang KY. Repairs of the rotator cuff. Correlation of functional results with integrity of the cuff. J Bone Joint Surg Am. 1991;73(7):982-989.
5. Bishop J, Klepps S, Lo IK, Bird J, Gladstone JN, Flatow EL. Cuff integrity after arthroscopic versus open rotator cuff repair: a prospective study. J Shoulder Elbow Surg. 2006;15(3):290-299.
6. Boileau P, Brassart N, Watkinson DJ, Carles M. Arthroscopic repair of full-thickness tears of the supraspinatus: does the tendon really heal? J Bone Joint Surg Am. 2005;87(6):1229-1240.
7. Gerber C, Fuchs B, Hodler J. The results of repair of massive tears of the rotator cuff. J Bone Joint Surg Am. 2000;82(4):505-515.
8. Lafosse L, Brozska R, Toussaint B, Gobezie R. The outcome and structural integrity of arthroscopic rotator cuff repair with use of the double-row suture anchor technique. J Bone Joint Surg Am. 2007;89(7):1533-1541.
9. Levy O, Venkateswaran B, Even T, Ravenscroft M, Copeland S. Mid-term clinical and sonographic outcome of arthroscopic repair of the rotator cuff. J Bone Joint Surg Br. 2008;90(10):1341-1347.
10. Zumstein MA, Jost B, Hempel J, Hodler J, Gerber C. The clinical and structural long-term results of open repair of massive tears of the rotator cuff. J Bone Joint Surg Am. 2008;90(11):2423-2431.
11. Gerber C, Schneeberger AG, Perren SM, Nyffeler RW. Experimental rotator cuff repair. A preliminary study. J Bone Joint Surg Am. 1999;81(9):1281-1290.
12. Randelli P, Arrigoni P, Ragone V, Aliprandi A, Cabitza P. Platelet rich plasma in arthroscopic rotator cuff repair: a prospective RCT study, 2-year follow-up. J Shoulder Elbow Surg. 2011;20(4):518-528.
13. Akeda K, An HS, Okuma M, et al. Platelet-rich plasma stimulates porcine articular chondrocyte proliferation and matrix biosynthesis. Osteoarthritis Cartilage. 2006;14(12):1272-1280.
14. de Mos M, van der Windt AE, Jahr H, et al. Can platelet-rich plasma enhance tendon repair? A cell culture study. Am J Sports Med. 2008;36(6):1171-1178.
15. Harmon KG. Muscle injuries and PRP: what does the science say? Br J Sports Med. 2010;44(9):616-617.
16. Kasten P, Vogel J, Geiger F, Niemeyer P, Luginbühl R, Szalay K. The effect of platelet-rich plasma on healing in critical-size long-bone defects. Biomaterials. 2008;29(29):3983-3992.
17. Mei-Dan O, Mann G, Maffulli N. Platelet-rich plasma: any substance into it? Br J Sports Med. 2010;44(9):618-619.
18. Murray MM, Spindler KP, Ballard P, Welch TP, Zurakowski D, Nanney LB. Enhanced histologic repair in a central wound in the anterior cruciate ligament with a collagen-platelet-rich plasma scaffold. J Orthop Res. 2007;25(8):1007-1017.
19. Virchenko O, Skoglund B, Aspenberg P. Parecoxib impairs early tendon repair but improves later remodeling. Am J Sports Med. 2004;32(7):1743-1747.
20. Aspenberg P. Differential inhibition of fracture healing by non-selective and cyclooxygenase-2 selective non-steroidal anti-inflammatory drugs. J Orthop Res. 2004;22(3):684.
21. Cohen DB, Kawamura S, Ehteshami JR, Rodeo SA. Indomethacin and celecoxib impair rotator cuff tendon-to-bone healing. Am J Sports Med. 2006;34(3):362-369.
22. Balazs T, Grice HC, Airth JM. On counting the blood cells of the rat with an electronic counter. Can J Comp Med Vet Sci. 1960;24(9):273-275.
23. Beck J, Evans D, Tonino PM, Yong S, Callaci JJ. The biomechanical and histologic effects of platelet-rich plasma on rat rotator cuff repairs. Am J Sports Med. 2012;40(9):2037-2044.
24. Aspenberg P, Virchenko O. Platelet concentrate injection improves Achilles tendon repair in rats. Acta Orthop Scand. 2004;75(1):93-99.
25. Chechik O, Dolkart O, Mozes G, Rak O, Alhajajra F, Maman E. Timing matters: NSAIDs interfere with the late proliferation stage of a repaired rotator cuff tendon healing in rats. Arch Orthop Trauma Surg. 2014;134(4):515-520.
26. Barber FA, Hrnack SA, Snyder SJ, Hapa O. Rotator cuff repair healing influenced by platelet-rich plasma construct augmentation. Arthroscopy. 2011;27(8):1029-1035.
27. Randelli PS, Arrigoni P, Cabitza P, Volpi P, Maffulli N. Autologous platelet rich plasma for arthroscopic rotator cuff repair. A pilot study. Disabil Rehabil. 2008;30(20-22):1584-1589.
28. Dolkart O, Chechik O, Zarfati Y, Brosh T, Alhajajra F, Maman E. A single dose of platelet-rich plasma improves the organization and strength of a surgically repaired rotator cuff tendon in rats. Arch Orthop Trauma Surg. 2014;134(9):1271-1277.
29. Castricini R, Longo UG, De Benedetto M, et al. Platelet-rich plasma augmentation for arthroscopic rotator cuff repair: a randomized controlled trial. Am J Sports Med. 2011;39(2):258-265.
30. Weber SC, Kauffman JI, Parise C, Weber SJ, Katz SD. Platelet-rich fibrin matrix in the management of arthroscopic repair of the rotator cuff: a prospective, randomized, double-blinded study. Am J Sports Med. 2013;41(2):263-270.
31. Ersen A, Demirhan M, Atalar AC, Kapicioğlu M, Baysal G. Platelet-rich plasma for enhancing surgical rotator cuff repair: evaluation and comparison of two application methods in a rat model. Arch Orthop Trauma Surg. 2014;134(3):405-411.
32. Warth RJ, Dornan GJ, James EW, Horan MP, Millett PJ. Clinical and structural outcomes after arthroscopic repair of full-thickness rotator cuff tears with and without platelet-rich product supplementation: a meta-analysis and meta-regression. Arthroscopy. 2015;31(2):306-320.
33. Bergeson AG, Tashjian RZ, Greis PE, Crim J, Stoddard GJ, Burks RT. Effects of platelet-rich fibrin matrix on repair integrity of at-risk rotator cuff tears. Am J Sports Med. 2012;40(2):286-293.
34. Riboh JC, Saltzman BM, Yanke AB, Fortier L, Cole BJ. Effect of leukocyte concentration on the efficacy of platelet-rich plasma in the treatment of knee osteoarthritis. Am J Sports Med. 2016;44(3):792-800.
Take-Home Points
- The optimal centrifugation protocol for production of rat PRP is 1300 rpm for 5 minutes.
- PRP administration in RCR improves tendon biomechanics in a rat model.
- Administration of NSAIDs following RCR has no significant effect on tendon biomechanical properties.
- NSAIDs may be co-administered with PRP without reducing efficacy of PRP.
- The role of PRP and NSAIDs in human RCR remains unclear.
Rotator cuff tears are a common source of shoulder pain and disability among older adults and athletes. Full-thickness tears alone occur in up to 30% of adults older than 60 years.1 Surgical repair is plagued by an unpredictable rate of recurrence (range, 11%-94%).1-10 As a result of improved suture materials, knotting patterns, and anchor designs, hardware issues are no longer the primary cause of rotator cuff repair (RCR) failures; now the principal mode of failure is biologic.2 Animal model studies have found that, after injury and subsequent healing, the tendon–bone interface remains abnormal.11 Rotator cuff research therefore has focused largely on biological enhancement of tendon-to-bone healing.
One means of biological augmentation is autologous platelet-rich plasma (PRP), which has supraphysiologic concentrations of platelets and their secreted growth factors. Although there is no consensus on the long-term efficacy of PRP, some studies suggest PRP accelerates healing over short and intermediate terms, which may contribute to a more rapid decrease in pain and more rapid return to normal activities.12-18 Similarly, systemic nonsteroidal anti-inflammatory drugs (NSAIDs) have long been used to treat musculoskeletal injuries, including rotator cuff pathology. However, NSAIDs inhibit cyclooxygenase activity, and clinical and experimental data have shown that cyclooxygenase 2 function is crucial in normal tendon-to-bone healing.19-21
Comprehensive studies have been conducted on the efficacy of both PRP and NSAIDs, but the interaction of concurrently used PRP and NSAIDs has not been determined. As many physicians use both modalities in the treatment of soft-tissue injuries, it is important to study the potential interactions when coadministered. Prior studies in small animal models suggest NSAIDs may impair tendon-to-bone healing in RCR, but there is no evidence regarding the effect of NSAIDs on the efficacy of PRP treatment.21
We conducted a study to determine the interaction of PRP and NSAIDs when used as adjuncts to RCR in a rat model. We hypothesized that PRP would increase the strength of RCR and that NSAIDs would interfere with the effects of PRP. A preliminary study objective was to determine an appropriate centrifugation protocol for producing PRP from rat blood, for use in this study and in future rat-based studies of PRP.
Materials and Methods
Part A: Pretesting Determination of PRP Centrifugation Protocol
Fourteen adult male Fischer rats were used in part A of this study, which was conducted to determine an appropriate PRP centrifugation protocol. Traditional PRP centrifugation protocols are established for human blood, but rat red blood cells (RBCs) and human RBCs differ in size.22 In our preliminary study, we wanted to determine the adjusted centrifuge speed and duration for producing clinically optimal PRP from rats. Clinically optimal PRP has reduced levels of RBCs, which decrease platelet affinity. Although the role of leukocytes in PRP preparations is debated, reducing the number of white blood cells (WBCs) decreases the number of matrix metalloproteinases and reactive oxygen species that may lead to inflammation. We used the platelet index (ratio of platelets to WBCs) and the RBC count to quantify the quality of our PRP sample.
Each rat in part A was anesthetized while supine. We used the Autologous Conditioned Plasma (ACP) system (Arthrex), which requires only 1 centrifugation cycle to create PRP. About 9 mL or 10 mL of blood was obtained by cardiac aspiration using an ACP Double Syringe (Arthrex). After blood retrieval, a thoracotomy was performed to confirm each rat’s death.
Part B: Determining the Effects of PRP and NSAIDs on RCR in a Rat Model
Operative Cohort. Of the 34 Fischer rats used in part B of this study, 6 were used as blood donors for PRP production, and the other 28 underwent bilateral rotator cuff surgeries. We used donor rats to maximize the amount of PRP retrieval, allocating about 1 donor rat per 5 operative rats. Fischer rats are an inbred strain, so the PRP from a donor Fischer rat simulates autologous blood in other Fischer rats. Use of allogenic blood is consistent with prior rat PRP studies.23,24
Operative Technique. Each bilateral surgery was performed by a single board-certified shoulder surgeon, and the anesthetic and surgical protocols were followed as approved by the home institution’s Institutional Animal Care and Use Committee. Before surgery, blood was harvested for PRP production from donor rats, as described earlier, and centrifuged for 5 minutes × 1300 rpm. After anesthetic induction and skin incision, the deltoid muscle was cut to expose the acromion and underlying rotator cuff. The distal supraspinatus tendon was sharply detached from the greater tuberosity. A bone-tunnel RCR was performed by drilling a transverse tunnel across the greater tuberosity and affixing the tendon to its footprint with a 5-0 polypropylene suture (Prolene; Ethicon). Each rat was then randomly assigned to receive 50 µL of donor PRP injected in 1 operative shoulder and saline in the contralateral shoulder. Injections were made in the supraspinatus tendon at its attachment to the humerus. Deltoid and skin were closed with 4-0 polyglactin (Vicryl) suture (Ethicon) and staples, respectively.
Tendon Preparation. Immediately post mortem, each shoulder was grossly dissected to isolate the supraspinatus muscle attached to the humerus. Shoulders were then frozen in 0.15-M saline solution until specified biomechanical testing dates.
On day of dimensional/biomechanical testing, each specimen was thawed at room temperature and finely dissected under a microscope (Stemi 200-C; Car Zeiss). After dissection, the humeral shaft was embedded in polymethylmethacrylate within a test tube. The free end of the supraspinatus tendon was glued within a “tab” of waterproofed emery cloth, leaving about 2 mm of tendon between the tab and the greater tuberosity.
Biomechanical Analysis. A 5848 MicroTester (Instron) was used for biomechanical testing. Each tabbed tendon, held by a pneumatic clamp attached to the MicroTester, was tested in a preconditioning phase and then a ramp-to-failure phase. A constant drip of 0.15-M saline was run through the apparatus to simulate physiologic hydration of tissue. After the embedded specimen was secure within the loading apparatus, an initial tensile preload of 0.2 N was applied. After preloading, the tendon was run through a preconditioning phase to account for viscoelastic relaxation. Immediately after preconditioning, each tendon was subjected to failure testing at a ramp rate of 0.1 mm/s. Force data were collected as a function of displacement, allowing for the calculation of 4 biomechanical parameters: failure force, tendon stiffness and normalized stiffness, energy to failure, and total energy. Tendon stiffness is the slope of a curve-fit line of the initial peak; failure force is the force of the highest peak; energy to failure is the area under the curve (AUC) to the highest peak; and total energy is the AUC from the start of failure ramping to the point at which the tendon is torn off completely. Two-way ANOVA was used to assess the differences between treatment groups and diet groups for all parameters. Statistical significance was set at P < .05.
A power analysis was performed to determine ability to detect differences between cohorts. For power of 80% and P = .05, a difference of 16% of the mean could be detected for failure force, 30% for energy to failure, 14% for total energy to failure, and 24% for stiffness. In addition, a difference of 4% of the mean could be detected for tendon length, 6% for width, and 10% for thickness.
Results
Across all collective treatment-diet groups and biomechanical parameters, there was only 1 statistically significant difference. Mean (SD) energy to failure was significantly higher (P = .03) in shoulders treated with PRP, 11.7 (7.3) N-mm, than in those treated without PRP, 8.7 (4.6) N-mm (Figure 4). There were no statistically significant differences between shoulders treated with indomethacin and those treated without indomethacin (Table 3), and no statistically significant relationships between treatment and drug for any other biomechanical parameter (Figures 5-7).
Discussion
Our preliminary objective in this study was to determine the optimal centrifugation protocol for producing rat-based PRP. Optimal PRP requires a dense concentration of platelets as well as reduced levels of RBCs and WBCs.25 We used the platelet index to quantify the quality of our PRP samples, and we obtained the highest platelet index for the protocol of 5 minutes × 1300 rpm. This finding may be useful in later rat studies involving PRP.
The primary objective of this study was to assess the effect of the interaction of PRP and NSAIDs on RCR. PRP has been found to augment RCR,12,26,27 but indomethacin may impair healing.21,25 We hypothesized that shoulders treated with PRP would have more biomechanical strength than control shoulders and that indomethacin would decrease biomechanical strength.
Our data showed increased energy to failure of the rotator cuff with PRP injections (P = .03). All other biomechanical parameters showed no significant differences with PRP treatment, though there were statistically insignificant trends of increased total energy, failure force, and stiffness in the PRP cohorts. There were no statistically significant differences between the indomethacin and no-indomethacin groups, and indomethacin had no effect on the efficacy of PRP treatment. It should be noted that the measurements of total energy, energy to failure, and failure force best reflect the strength of the tendon–bone interface. Other biomechanical measures, such as stiffness and normalized stiffness, are physical properties of the tendon itself and apply less to enthesis strength, which was the primary focus of this study.
Beck and colleagues23 studied the effect of allogeneic PRP on RCR in a rat model. They tested biomechanical and histologic outcomes 7, 14, and 21 days after surgery. There was no significant difference in failure load between the 2 groups at any time point. Compared with failure strain in the control group, failure strain in the PRP group was decreased at 7 days, normalized at 14 days, and increased at 21 days. The authors hypothesized that increased tendon failure strain at 21 days may have reduced forces being transmitted to the suture fixation site, which may be clinically significant and warrants further investigation. In a similar study, by Dolkart and colleagues,28 intraoperative PRP administration enhanced the maximal load-to-failure and stiffness of rats’ repaired rotator cuffs. On histologic examination, tendons treated with PRP (vs control tendons) had more organized collagen. Although these studies have limitations similar to our study, these results further support improved tendon-to-bone healing with PRP.
In clinical application, Barber and colleagues26 found that, compared with controls, suturing PRP fibrin matrix into the rotator cuff during repair decreased the incidence of magnetic resonance imaging–detected retears. However, in 2 prospective, randomized trials, Castricini and colleagues29 and Weber and colleagues30 found that use of PRP in RCR did not improve outcomes. All 3 studies differ from ours in that they used fibrin matrix. However, Ersen and colleagues31 found no difference in the effects of PRP on rotator cuff healing between injection and fibrin matrix; PRP improved biomechanical properties of repaired rotator cuff independent of administration method. In a meta-analysis of PRP supplementation in RCR, Warth and colleagues32 found a statistically significant improvement in retear rates for tears >3 cm repaired with a double-row technique, but otherwise no overall improvement in retear rates or outcome scores with PRP. The authors acknowledged that the significant heterogeneity of the studies in their meta-analysis may have affected the quality of their data.
Although our study provides some insight into the effectiveness of PRP in tendon repair, the lack of standardization in PRP preparation and time points tested makes comparisons with similar studies difficult.33 Recent reports have emphasized that not all PRP separation systems yield similar products.33 Platelet concentrations, and therefore platelet-derived growth factor concentrations, differ between systems and may yield different clinical outcomes. Our decision to use leukocyte-reduced PRP is supported by a meta-analysis by Riboh and colleagues,34 who reviewed the literature on the effect of leukocyte concentration on the efficacy of PRP products. They found that, in the treatment of knee osteoarthritis, use of leukocyte-poor PRP resulted in improved functional outcomes scores in comparison with placebo, but this improvement did not occur with leukocyte-rich PRP. However, there is still no consensus on optimal preparation, dosing, and route of administration of PRP, and preparations described in the literature vary.
This study also assessed the interaction of PRP and NSAIDs. Although there were no statistically significant differences between treatment and diet, shoulders treated with indomethacin alone showed a trend toward weaker biomechanical parameters in comparison with shoulders treated with saline alone, with PRP alone, or with both PRP and indomethacin. A larger sample would be needed to establish statistical significance. These trends are not surprising, as Cohen and colleagues21 found that NSAIDs, specifically indomethacin and celecoxib, significantly inhibited rotator cuff tendon-to-bone healing. The authors also found that a 2-week course of indomethacin was sufficient to significantly inhibit tendon-to-bone healing. In fact, although the drugs were discontinued after 14 days, biomechanical properties were negatively affected up to 8 weeks after repair. Our results differ from theirs even though the 2 studies used similar doses and administration protocols.
One strength of this study was that all surgeries were performed by a single board-certified surgeon using a standardized technique. In addition, a control group was established, and personnel and techniques for all fine dissections and biomechanical tests were consistent throughout. Blinded randomization and diet normalization, as well as adequate power for detecting significant effects, strengthened the study as well.
The study had several limitations. First, whereas most human rotator cuff tears are chronic, we used a model of acute injury and repair. As acute tears that are immediately repaired are more likely to heal, detection of differences between cohorts is less likely. However, using an acute model is still the most reliable strategy for inducing a controlled injury with reproducible severity. Second, we analyzed data at only 1 time point, which may not provide an accurate representation of long-term effects. Third, systemic administration of indomethacin did not allow for intra-rat shoulder comparisons of the different drug groups. Fourth, although it is possible that the dosage of NSAID was insufficient to produce significant differences in biomechanics, our dosage was consistent with that used in a study that found a significant effect on tendon healing.21
Conclusion
Our study found that the strength of the supraspinatus tendon enthesis as defined by energy to failure was increased with intratendinous PRP injection. Indomethacin showed no statistical effect, but there was a trend toward reduced strength after repair. However, the extent to which coadministration of indomethacin affects PRP remains unclear, and these data cannot necessarily be extrapolated to the typical human rotator cuff tear caused by chronic repetitive stress.
Take-Home Points
- The optimal centrifugation protocol for production of rat PRP is 1300 rpm for 5 minutes.
- PRP administration in RCR improves tendon biomechanics in a rat model.
- Administration of NSAIDs following RCR has no significant effect on tendon biomechanical properties.
- NSAIDs may be co-administered with PRP without reducing efficacy of PRP.
- The role of PRP and NSAIDs in human RCR remains unclear.
Rotator cuff tears are a common source of shoulder pain and disability among older adults and athletes. Full-thickness tears alone occur in up to 30% of adults older than 60 years.1 Surgical repair is plagued by an unpredictable rate of recurrence (range, 11%-94%).1-10 As a result of improved suture materials, knotting patterns, and anchor designs, hardware issues are no longer the primary cause of rotator cuff repair (RCR) failures; now the principal mode of failure is biologic.2 Animal model studies have found that, after injury and subsequent healing, the tendon–bone interface remains abnormal.11 Rotator cuff research therefore has focused largely on biological enhancement of tendon-to-bone healing.
One means of biological augmentation is autologous platelet-rich plasma (PRP), which has supraphysiologic concentrations of platelets and their secreted growth factors. Although there is no consensus on the long-term efficacy of PRP, some studies suggest PRP accelerates healing over short and intermediate terms, which may contribute to a more rapid decrease in pain and more rapid return to normal activities.12-18 Similarly, systemic nonsteroidal anti-inflammatory drugs (NSAIDs) have long been used to treat musculoskeletal injuries, including rotator cuff pathology. However, NSAIDs inhibit cyclooxygenase activity, and clinical and experimental data have shown that cyclooxygenase 2 function is crucial in normal tendon-to-bone healing.19-21
Comprehensive studies have been conducted on the efficacy of both PRP and NSAIDs, but the interaction of concurrently used PRP and NSAIDs has not been determined. As many physicians use both modalities in the treatment of soft-tissue injuries, it is important to study the potential interactions when coadministered. Prior studies in small animal models suggest NSAIDs may impair tendon-to-bone healing in RCR, but there is no evidence regarding the effect of NSAIDs on the efficacy of PRP treatment.21
We conducted a study to determine the interaction of PRP and NSAIDs when used as adjuncts to RCR in a rat model. We hypothesized that PRP would increase the strength of RCR and that NSAIDs would interfere with the effects of PRP. A preliminary study objective was to determine an appropriate centrifugation protocol for producing PRP from rat blood, for use in this study and in future rat-based studies of PRP.
Materials and Methods
Part A: Pretesting Determination of PRP Centrifugation Protocol
Fourteen adult male Fischer rats were used in part A of this study, which was conducted to determine an appropriate PRP centrifugation protocol. Traditional PRP centrifugation protocols are established for human blood, but rat red blood cells (RBCs) and human RBCs differ in size.22 In our preliminary study, we wanted to determine the adjusted centrifuge speed and duration for producing clinically optimal PRP from rats. Clinically optimal PRP has reduced levels of RBCs, which decrease platelet affinity. Although the role of leukocytes in PRP preparations is debated, reducing the number of white blood cells (WBCs) decreases the number of matrix metalloproteinases and reactive oxygen species that may lead to inflammation. We used the platelet index (ratio of platelets to WBCs) and the RBC count to quantify the quality of our PRP sample.
Each rat in part A was anesthetized while supine. We used the Autologous Conditioned Plasma (ACP) system (Arthrex), which requires only 1 centrifugation cycle to create PRP. About 9 mL or 10 mL of blood was obtained by cardiac aspiration using an ACP Double Syringe (Arthrex). After blood retrieval, a thoracotomy was performed to confirm each rat’s death.
Part B: Determining the Effects of PRP and NSAIDs on RCR in a Rat Model
Operative Cohort. Of the 34 Fischer rats used in part B of this study, 6 were used as blood donors for PRP production, and the other 28 underwent bilateral rotator cuff surgeries. We used donor rats to maximize the amount of PRP retrieval, allocating about 1 donor rat per 5 operative rats. Fischer rats are an inbred strain, so the PRP from a donor Fischer rat simulates autologous blood in other Fischer rats. Use of allogenic blood is consistent with prior rat PRP studies.23,24
Operative Technique. Each bilateral surgery was performed by a single board-certified shoulder surgeon, and the anesthetic and surgical protocols were followed as approved by the home institution’s Institutional Animal Care and Use Committee. Before surgery, blood was harvested for PRP production from donor rats, as described earlier, and centrifuged for 5 minutes × 1300 rpm. After anesthetic induction and skin incision, the deltoid muscle was cut to expose the acromion and underlying rotator cuff. The distal supraspinatus tendon was sharply detached from the greater tuberosity. A bone-tunnel RCR was performed by drilling a transverse tunnel across the greater tuberosity and affixing the tendon to its footprint with a 5-0 polypropylene suture (Prolene; Ethicon). Each rat was then randomly assigned to receive 50 µL of donor PRP injected in 1 operative shoulder and saline in the contralateral shoulder. Injections were made in the supraspinatus tendon at its attachment to the humerus. Deltoid and skin were closed with 4-0 polyglactin (Vicryl) suture (Ethicon) and staples, respectively.
Tendon Preparation. Immediately post mortem, each shoulder was grossly dissected to isolate the supraspinatus muscle attached to the humerus. Shoulders were then frozen in 0.15-M saline solution until specified biomechanical testing dates.
On day of dimensional/biomechanical testing, each specimen was thawed at room temperature and finely dissected under a microscope (Stemi 200-C; Car Zeiss). After dissection, the humeral shaft was embedded in polymethylmethacrylate within a test tube. The free end of the supraspinatus tendon was glued within a “tab” of waterproofed emery cloth, leaving about 2 mm of tendon between the tab and the greater tuberosity.
Biomechanical Analysis. A 5848 MicroTester (Instron) was used for biomechanical testing. Each tabbed tendon, held by a pneumatic clamp attached to the MicroTester, was tested in a preconditioning phase and then a ramp-to-failure phase. A constant drip of 0.15-M saline was run through the apparatus to simulate physiologic hydration of tissue. After the embedded specimen was secure within the loading apparatus, an initial tensile preload of 0.2 N was applied. After preloading, the tendon was run through a preconditioning phase to account for viscoelastic relaxation. Immediately after preconditioning, each tendon was subjected to failure testing at a ramp rate of 0.1 mm/s. Force data were collected as a function of displacement, allowing for the calculation of 4 biomechanical parameters: failure force, tendon stiffness and normalized stiffness, energy to failure, and total energy. Tendon stiffness is the slope of a curve-fit line of the initial peak; failure force is the force of the highest peak; energy to failure is the area under the curve (AUC) to the highest peak; and total energy is the AUC from the start of failure ramping to the point at which the tendon is torn off completely. Two-way ANOVA was used to assess the differences between treatment groups and diet groups for all parameters. Statistical significance was set at P < .05.
A power analysis was performed to determine ability to detect differences between cohorts. For power of 80% and P = .05, a difference of 16% of the mean could be detected for failure force, 30% for energy to failure, 14% for total energy to failure, and 24% for stiffness. In addition, a difference of 4% of the mean could be detected for tendon length, 6% for width, and 10% for thickness.
Results
Across all collective treatment-diet groups and biomechanical parameters, there was only 1 statistically significant difference. Mean (SD) energy to failure was significantly higher (P = .03) in shoulders treated with PRP, 11.7 (7.3) N-mm, than in those treated without PRP, 8.7 (4.6) N-mm (Figure 4). There were no statistically significant differences between shoulders treated with indomethacin and those treated without indomethacin (Table 3), and no statistically significant relationships between treatment and drug for any other biomechanical parameter (Figures 5-7).
Discussion
Our preliminary objective in this study was to determine the optimal centrifugation protocol for producing rat-based PRP. Optimal PRP requires a dense concentration of platelets as well as reduced levels of RBCs and WBCs.25 We used the platelet index to quantify the quality of our PRP samples, and we obtained the highest platelet index for the protocol of 5 minutes × 1300 rpm. This finding may be useful in later rat studies involving PRP.
The primary objective of this study was to assess the effect of the interaction of PRP and NSAIDs on RCR. PRP has been found to augment RCR,12,26,27 but indomethacin may impair healing.21,25 We hypothesized that shoulders treated with PRP would have more biomechanical strength than control shoulders and that indomethacin would decrease biomechanical strength.
Our data showed increased energy to failure of the rotator cuff with PRP injections (P = .03). All other biomechanical parameters showed no significant differences with PRP treatment, though there were statistically insignificant trends of increased total energy, failure force, and stiffness in the PRP cohorts. There were no statistically significant differences between the indomethacin and no-indomethacin groups, and indomethacin had no effect on the efficacy of PRP treatment. It should be noted that the measurements of total energy, energy to failure, and failure force best reflect the strength of the tendon–bone interface. Other biomechanical measures, such as stiffness and normalized stiffness, are physical properties of the tendon itself and apply less to enthesis strength, which was the primary focus of this study.
Beck and colleagues23 studied the effect of allogeneic PRP on RCR in a rat model. They tested biomechanical and histologic outcomes 7, 14, and 21 days after surgery. There was no significant difference in failure load between the 2 groups at any time point. Compared with failure strain in the control group, failure strain in the PRP group was decreased at 7 days, normalized at 14 days, and increased at 21 days. The authors hypothesized that increased tendon failure strain at 21 days may have reduced forces being transmitted to the suture fixation site, which may be clinically significant and warrants further investigation. In a similar study, by Dolkart and colleagues,28 intraoperative PRP administration enhanced the maximal load-to-failure and stiffness of rats’ repaired rotator cuffs. On histologic examination, tendons treated with PRP (vs control tendons) had more organized collagen. Although these studies have limitations similar to our study, these results further support improved tendon-to-bone healing with PRP.
In clinical application, Barber and colleagues26 found that, compared with controls, suturing PRP fibrin matrix into the rotator cuff during repair decreased the incidence of magnetic resonance imaging–detected retears. However, in 2 prospective, randomized trials, Castricini and colleagues29 and Weber and colleagues30 found that use of PRP in RCR did not improve outcomes. All 3 studies differ from ours in that they used fibrin matrix. However, Ersen and colleagues31 found no difference in the effects of PRP on rotator cuff healing between injection and fibrin matrix; PRP improved biomechanical properties of repaired rotator cuff independent of administration method. In a meta-analysis of PRP supplementation in RCR, Warth and colleagues32 found a statistically significant improvement in retear rates for tears >3 cm repaired with a double-row technique, but otherwise no overall improvement in retear rates or outcome scores with PRP. The authors acknowledged that the significant heterogeneity of the studies in their meta-analysis may have affected the quality of their data.
Although our study provides some insight into the effectiveness of PRP in tendon repair, the lack of standardization in PRP preparation and time points tested makes comparisons with similar studies difficult.33 Recent reports have emphasized that not all PRP separation systems yield similar products.33 Platelet concentrations, and therefore platelet-derived growth factor concentrations, differ between systems and may yield different clinical outcomes. Our decision to use leukocyte-reduced PRP is supported by a meta-analysis by Riboh and colleagues,34 who reviewed the literature on the effect of leukocyte concentration on the efficacy of PRP products. They found that, in the treatment of knee osteoarthritis, use of leukocyte-poor PRP resulted in improved functional outcomes scores in comparison with placebo, but this improvement did not occur with leukocyte-rich PRP. However, there is still no consensus on optimal preparation, dosing, and route of administration of PRP, and preparations described in the literature vary.
This study also assessed the interaction of PRP and NSAIDs. Although there were no statistically significant differences between treatment and diet, shoulders treated with indomethacin alone showed a trend toward weaker biomechanical parameters in comparison with shoulders treated with saline alone, with PRP alone, or with both PRP and indomethacin. A larger sample would be needed to establish statistical significance. These trends are not surprising, as Cohen and colleagues21 found that NSAIDs, specifically indomethacin and celecoxib, significantly inhibited rotator cuff tendon-to-bone healing. The authors also found that a 2-week course of indomethacin was sufficient to significantly inhibit tendon-to-bone healing. In fact, although the drugs were discontinued after 14 days, biomechanical properties were negatively affected up to 8 weeks after repair. Our results differ from theirs even though the 2 studies used similar doses and administration protocols.
One strength of this study was that all surgeries were performed by a single board-certified surgeon using a standardized technique. In addition, a control group was established, and personnel and techniques for all fine dissections and biomechanical tests were consistent throughout. Blinded randomization and diet normalization, as well as adequate power for detecting significant effects, strengthened the study as well.
The study had several limitations. First, whereas most human rotator cuff tears are chronic, we used a model of acute injury and repair. As acute tears that are immediately repaired are more likely to heal, detection of differences between cohorts is less likely. However, using an acute model is still the most reliable strategy for inducing a controlled injury with reproducible severity. Second, we analyzed data at only 1 time point, which may not provide an accurate representation of long-term effects. Third, systemic administration of indomethacin did not allow for intra-rat shoulder comparisons of the different drug groups. Fourth, although it is possible that the dosage of NSAID was insufficient to produce significant differences in biomechanics, our dosage was consistent with that used in a study that found a significant effect on tendon healing.21
Conclusion
Our study found that the strength of the supraspinatus tendon enthesis as defined by energy to failure was increased with intratendinous PRP injection. Indomethacin showed no statistical effect, but there was a trend toward reduced strength after repair. However, the extent to which coadministration of indomethacin affects PRP remains unclear, and these data cannot necessarily be extrapolated to the typical human rotator cuff tear caused by chronic repetitive stress.
1. Kinsella KG, Velkoff VA. An Aging World: 2001. Washington, DC: US Government Printing Office; 2001. https://www.census.gov/prod/2001pubs/p95-01-1.pdf. Published November 2001. Accessed September 24, 2017.
2. Gamradt SC, Rodeo SA, Warren RF. Platelet rich plasma in rotator cuff repair. Tech Orthop. 2007;22(1):26-33.
3. Galatz LM, Ball CM, Teefey SA, Middleton WD, Yamaguchi K. The outcome and repair integrity of completely arthroscopically repaired large and massive rotator cuff tears. J Bone Joint Surg Am. 2004;86(2):219-224.
4. Harryman DT, Mack LA, Wang KY. Repairs of the rotator cuff. Correlation of functional results with integrity of the cuff. J Bone Joint Surg Am. 1991;73(7):982-989.
5. Bishop J, Klepps S, Lo IK, Bird J, Gladstone JN, Flatow EL. Cuff integrity after arthroscopic versus open rotator cuff repair: a prospective study. J Shoulder Elbow Surg. 2006;15(3):290-299.
6. Boileau P, Brassart N, Watkinson DJ, Carles M. Arthroscopic repair of full-thickness tears of the supraspinatus: does the tendon really heal? J Bone Joint Surg Am. 2005;87(6):1229-1240.
7. Gerber C, Fuchs B, Hodler J. The results of repair of massive tears of the rotator cuff. J Bone Joint Surg Am. 2000;82(4):505-515.
8. Lafosse L, Brozska R, Toussaint B, Gobezie R. The outcome and structural integrity of arthroscopic rotator cuff repair with use of the double-row suture anchor technique. J Bone Joint Surg Am. 2007;89(7):1533-1541.
9. Levy O, Venkateswaran B, Even T, Ravenscroft M, Copeland S. Mid-term clinical and sonographic outcome of arthroscopic repair of the rotator cuff. J Bone Joint Surg Br. 2008;90(10):1341-1347.
10. Zumstein MA, Jost B, Hempel J, Hodler J, Gerber C. The clinical and structural long-term results of open repair of massive tears of the rotator cuff. J Bone Joint Surg Am. 2008;90(11):2423-2431.
11. Gerber C, Schneeberger AG, Perren SM, Nyffeler RW. Experimental rotator cuff repair. A preliminary study. J Bone Joint Surg Am. 1999;81(9):1281-1290.
12. Randelli P, Arrigoni P, Ragone V, Aliprandi A, Cabitza P. Platelet rich plasma in arthroscopic rotator cuff repair: a prospective RCT study, 2-year follow-up. J Shoulder Elbow Surg. 2011;20(4):518-528.
13. Akeda K, An HS, Okuma M, et al. Platelet-rich plasma stimulates porcine articular chondrocyte proliferation and matrix biosynthesis. Osteoarthritis Cartilage. 2006;14(12):1272-1280.
14. de Mos M, van der Windt AE, Jahr H, et al. Can platelet-rich plasma enhance tendon repair? A cell culture study. Am J Sports Med. 2008;36(6):1171-1178.
15. Harmon KG. Muscle injuries and PRP: what does the science say? Br J Sports Med. 2010;44(9):616-617.
16. Kasten P, Vogel J, Geiger F, Niemeyer P, Luginbühl R, Szalay K. The effect of platelet-rich plasma on healing in critical-size long-bone defects. Biomaterials. 2008;29(29):3983-3992.
17. Mei-Dan O, Mann G, Maffulli N. Platelet-rich plasma: any substance into it? Br J Sports Med. 2010;44(9):618-619.
18. Murray MM, Spindler KP, Ballard P, Welch TP, Zurakowski D, Nanney LB. Enhanced histologic repair in a central wound in the anterior cruciate ligament with a collagen-platelet-rich plasma scaffold. J Orthop Res. 2007;25(8):1007-1017.
19. Virchenko O, Skoglund B, Aspenberg P. Parecoxib impairs early tendon repair but improves later remodeling. Am J Sports Med. 2004;32(7):1743-1747.
20. Aspenberg P. Differential inhibition of fracture healing by non-selective and cyclooxygenase-2 selective non-steroidal anti-inflammatory drugs. J Orthop Res. 2004;22(3):684.
21. Cohen DB, Kawamura S, Ehteshami JR, Rodeo SA. Indomethacin and celecoxib impair rotator cuff tendon-to-bone healing. Am J Sports Med. 2006;34(3):362-369.
22. Balazs T, Grice HC, Airth JM. On counting the blood cells of the rat with an electronic counter. Can J Comp Med Vet Sci. 1960;24(9):273-275.
23. Beck J, Evans D, Tonino PM, Yong S, Callaci JJ. The biomechanical and histologic effects of platelet-rich plasma on rat rotator cuff repairs. Am J Sports Med. 2012;40(9):2037-2044.
24. Aspenberg P, Virchenko O. Platelet concentrate injection improves Achilles tendon repair in rats. Acta Orthop Scand. 2004;75(1):93-99.
25. Chechik O, Dolkart O, Mozes G, Rak O, Alhajajra F, Maman E. Timing matters: NSAIDs interfere with the late proliferation stage of a repaired rotator cuff tendon healing in rats. Arch Orthop Trauma Surg. 2014;134(4):515-520.
26. Barber FA, Hrnack SA, Snyder SJ, Hapa O. Rotator cuff repair healing influenced by platelet-rich plasma construct augmentation. Arthroscopy. 2011;27(8):1029-1035.
27. Randelli PS, Arrigoni P, Cabitza P, Volpi P, Maffulli N. Autologous platelet rich plasma for arthroscopic rotator cuff repair. A pilot study. Disabil Rehabil. 2008;30(20-22):1584-1589.
28. Dolkart O, Chechik O, Zarfati Y, Brosh T, Alhajajra F, Maman E. A single dose of platelet-rich plasma improves the organization and strength of a surgically repaired rotator cuff tendon in rats. Arch Orthop Trauma Surg. 2014;134(9):1271-1277.
29. Castricini R, Longo UG, De Benedetto M, et al. Platelet-rich plasma augmentation for arthroscopic rotator cuff repair: a randomized controlled trial. Am J Sports Med. 2011;39(2):258-265.
30. Weber SC, Kauffman JI, Parise C, Weber SJ, Katz SD. Platelet-rich fibrin matrix in the management of arthroscopic repair of the rotator cuff: a prospective, randomized, double-blinded study. Am J Sports Med. 2013;41(2):263-270.
31. Ersen A, Demirhan M, Atalar AC, Kapicioğlu M, Baysal G. Platelet-rich plasma for enhancing surgical rotator cuff repair: evaluation and comparison of two application methods in a rat model. Arch Orthop Trauma Surg. 2014;134(3):405-411.
32. Warth RJ, Dornan GJ, James EW, Horan MP, Millett PJ. Clinical and structural outcomes after arthroscopic repair of full-thickness rotator cuff tears with and without platelet-rich product supplementation: a meta-analysis and meta-regression. Arthroscopy. 2015;31(2):306-320.
33. Bergeson AG, Tashjian RZ, Greis PE, Crim J, Stoddard GJ, Burks RT. Effects of platelet-rich fibrin matrix on repair integrity of at-risk rotator cuff tears. Am J Sports Med. 2012;40(2):286-293.
34. Riboh JC, Saltzman BM, Yanke AB, Fortier L, Cole BJ. Effect of leukocyte concentration on the efficacy of platelet-rich plasma in the treatment of knee osteoarthritis. Am J Sports Med. 2016;44(3):792-800.
1. Kinsella KG, Velkoff VA. An Aging World: 2001. Washington, DC: US Government Printing Office; 2001. https://www.census.gov/prod/2001pubs/p95-01-1.pdf. Published November 2001. Accessed September 24, 2017.
2. Gamradt SC, Rodeo SA, Warren RF. Platelet rich plasma in rotator cuff repair. Tech Orthop. 2007;22(1):26-33.
3. Galatz LM, Ball CM, Teefey SA, Middleton WD, Yamaguchi K. The outcome and repair integrity of completely arthroscopically repaired large and massive rotator cuff tears. J Bone Joint Surg Am. 2004;86(2):219-224.
4. Harryman DT, Mack LA, Wang KY. Repairs of the rotator cuff. Correlation of functional results with integrity of the cuff. J Bone Joint Surg Am. 1991;73(7):982-989.
5. Bishop J, Klepps S, Lo IK, Bird J, Gladstone JN, Flatow EL. Cuff integrity after arthroscopic versus open rotator cuff repair: a prospective study. J Shoulder Elbow Surg. 2006;15(3):290-299.
6. Boileau P, Brassart N, Watkinson DJ, Carles M. Arthroscopic repair of full-thickness tears of the supraspinatus: does the tendon really heal? J Bone Joint Surg Am. 2005;87(6):1229-1240.
7. Gerber C, Fuchs B, Hodler J. The results of repair of massive tears of the rotator cuff. J Bone Joint Surg Am. 2000;82(4):505-515.
8. Lafosse L, Brozska R, Toussaint B, Gobezie R. The outcome and structural integrity of arthroscopic rotator cuff repair with use of the double-row suture anchor technique. J Bone Joint Surg Am. 2007;89(7):1533-1541.
9. Levy O, Venkateswaran B, Even T, Ravenscroft M, Copeland S. Mid-term clinical and sonographic outcome of arthroscopic repair of the rotator cuff. J Bone Joint Surg Br. 2008;90(10):1341-1347.
10. Zumstein MA, Jost B, Hempel J, Hodler J, Gerber C. The clinical and structural long-term results of open repair of massive tears of the rotator cuff. J Bone Joint Surg Am. 2008;90(11):2423-2431.
11. Gerber C, Schneeberger AG, Perren SM, Nyffeler RW. Experimental rotator cuff repair. A preliminary study. J Bone Joint Surg Am. 1999;81(9):1281-1290.
12. Randelli P, Arrigoni P, Ragone V, Aliprandi A, Cabitza P. Platelet rich plasma in arthroscopic rotator cuff repair: a prospective RCT study, 2-year follow-up. J Shoulder Elbow Surg. 2011;20(4):518-528.
13. Akeda K, An HS, Okuma M, et al. Platelet-rich plasma stimulates porcine articular chondrocyte proliferation and matrix biosynthesis. Osteoarthritis Cartilage. 2006;14(12):1272-1280.
14. de Mos M, van der Windt AE, Jahr H, et al. Can platelet-rich plasma enhance tendon repair? A cell culture study. Am J Sports Med. 2008;36(6):1171-1178.
15. Harmon KG. Muscle injuries and PRP: what does the science say? Br J Sports Med. 2010;44(9):616-617.
16. Kasten P, Vogel J, Geiger F, Niemeyer P, Luginbühl R, Szalay K. The effect of platelet-rich plasma on healing in critical-size long-bone defects. Biomaterials. 2008;29(29):3983-3992.
17. Mei-Dan O, Mann G, Maffulli N. Platelet-rich plasma: any substance into it? Br J Sports Med. 2010;44(9):618-619.
18. Murray MM, Spindler KP, Ballard P, Welch TP, Zurakowski D, Nanney LB. Enhanced histologic repair in a central wound in the anterior cruciate ligament with a collagen-platelet-rich plasma scaffold. J Orthop Res. 2007;25(8):1007-1017.
19. Virchenko O, Skoglund B, Aspenberg P. Parecoxib impairs early tendon repair but improves later remodeling. Am J Sports Med. 2004;32(7):1743-1747.
20. Aspenberg P. Differential inhibition of fracture healing by non-selective and cyclooxygenase-2 selective non-steroidal anti-inflammatory drugs. J Orthop Res. 2004;22(3):684.
21. Cohen DB, Kawamura S, Ehteshami JR, Rodeo SA. Indomethacin and celecoxib impair rotator cuff tendon-to-bone healing. Am J Sports Med. 2006;34(3):362-369.
22. Balazs T, Grice HC, Airth JM. On counting the blood cells of the rat with an electronic counter. Can J Comp Med Vet Sci. 1960;24(9):273-275.
23. Beck J, Evans D, Tonino PM, Yong S, Callaci JJ. The biomechanical and histologic effects of platelet-rich plasma on rat rotator cuff repairs. Am J Sports Med. 2012;40(9):2037-2044.
24. Aspenberg P, Virchenko O. Platelet concentrate injection improves Achilles tendon repair in rats. Acta Orthop Scand. 2004;75(1):93-99.
25. Chechik O, Dolkart O, Mozes G, Rak O, Alhajajra F, Maman E. Timing matters: NSAIDs interfere with the late proliferation stage of a repaired rotator cuff tendon healing in rats. Arch Orthop Trauma Surg. 2014;134(4):515-520.
26. Barber FA, Hrnack SA, Snyder SJ, Hapa O. Rotator cuff repair healing influenced by platelet-rich plasma construct augmentation. Arthroscopy. 2011;27(8):1029-1035.
27. Randelli PS, Arrigoni P, Cabitza P, Volpi P, Maffulli N. Autologous platelet rich plasma for arthroscopic rotator cuff repair. A pilot study. Disabil Rehabil. 2008;30(20-22):1584-1589.
28. Dolkart O, Chechik O, Zarfati Y, Brosh T, Alhajajra F, Maman E. A single dose of platelet-rich plasma improves the organization and strength of a surgically repaired rotator cuff tendon in rats. Arch Orthop Trauma Surg. 2014;134(9):1271-1277.
29. Castricini R, Longo UG, De Benedetto M, et al. Platelet-rich plasma augmentation for arthroscopic rotator cuff repair: a randomized controlled trial. Am J Sports Med. 2011;39(2):258-265.
30. Weber SC, Kauffman JI, Parise C, Weber SJ, Katz SD. Platelet-rich fibrin matrix in the management of arthroscopic repair of the rotator cuff: a prospective, randomized, double-blinded study. Am J Sports Med. 2013;41(2):263-270.
31. Ersen A, Demirhan M, Atalar AC, Kapicioğlu M, Baysal G. Platelet-rich plasma for enhancing surgical rotator cuff repair: evaluation and comparison of two application methods in a rat model. Arch Orthop Trauma Surg. 2014;134(3):405-411.
32. Warth RJ, Dornan GJ, James EW, Horan MP, Millett PJ. Clinical and structural outcomes after arthroscopic repair of full-thickness rotator cuff tears with and without platelet-rich product supplementation: a meta-analysis and meta-regression. Arthroscopy. 2015;31(2):306-320.
33. Bergeson AG, Tashjian RZ, Greis PE, Crim J, Stoddard GJ, Burks RT. Effects of platelet-rich fibrin matrix on repair integrity of at-risk rotator cuff tears. Am J Sports Med. 2012;40(2):286-293.
34. Riboh JC, Saltzman BM, Yanke AB, Fortier L, Cole BJ. Effect of leukocyte concentration on the efficacy of platelet-rich plasma in the treatment of knee osteoarthritis. Am J Sports Med. 2016;44(3):792-800.
Reliability of 3-Dimensional Glenoid Component Templating and Correlation to Intraoperative Component Selection
Take-Home Points
- Guidelines regarding glenoid component size selection for primary TSA are lacking.
- Intraoperative in situ glenoid sizing may not be ideal.
- 3-D digital models may be utilized for preoperative templating of glenoid component size in primary TSA.
- 3-D templating that allows for superior-inferior, anterior-posterior, and rotational translation can lead to consistent and reproducible templating of glenoid component size.
- 3-D templating may reduce the risks of implant overhang, peg penetration, and decreased stability ratio.
In 1974, Neer1 introduced the shoulder prosthesis. In 1982, Neer and colleagues2 found significant improvement in shoulder pain and function in patients with glenohumeral osteoarthritis treated with the Neer prosthesis. Since then, use of total shoulder arthroplasty (TSA) has increased. Between 1993 and 2007, TSA use increased 319% in the United States.3 Long-term outcomes studies have found implant survivorship ranging from 87% to 93% at 10 to 15 years.4
Although TSA is a successful procedure, glenoid component failure is the most common complication.5-10 Outcomes of revision surgery for glenoid instability are inferior to those of primary TSA.11 Recent research findings highlight the effect of glenoid size on TSA complications.12 A larger glenoid component increases the stability ratio (peak subluxation force divided by compression load).12 However, insufficient glenoid bone stock, small glenoid diameter, and inability to fit a properly sized reamer owing to soft-tissue constraints may lead surgeons to choose a smaller glenoid component in order to avoid peg penetration, overhang, and soft-tissue damage, respectively. Therefore, preoperative templating of glenoid size is a potential strategy for minimizing complications.
Templating is performed for proximal humeral components, but glenoid sizing typically is deferred to intraoperative in situ sizing with implant-specific targeting guides. This glenoid sizing practice arose out of a lack of standard digital glenoid templates and difficulty in selecting glenoid size based on plain radiographs and/or 2-dimensional (2-D) computed tomography (CT) scans. However, targeting devices are sporadically used during surgery, and intraoperative glenoid vault dimension estimates derived from visualization and palpation are often inaccurate. Often, rather than directly assess glenoid morphology, surgeons infer glenoid size from the size and sex of patients.13
Three-dimensional (3-D) CT can be used to accurately assess glenoid version, bone loss, and implant fit.14-19 We conducted a study to determine if 3-D digital imaging can be consistently and reproducibly used for preoperative templating of glenoid component size and to determine if glenoid sizes derived from templating correlate with the sizes of subsequently implanted glenoids.
Materials and Methods
This retrospective study was conducted at the Center for Shoulder, Elbow, and Sports Medicine at Columbia University Medical Center in New York City and was approved by our Institutional Review Board. Included in the study were all patients who underwent primary TSA for primary glenohumeral osteoarthritis over a 12-month period. Patients were required to have preoperative CT performed according to our study protocol. The CT protocol consisted of 0.5-mm axial cuts of the entire scapula and 3-D reconstruction of the scapula, glenoid, glenohumeral articulation, and proximal humerus. Patients were excluded from the study for primary TSA for a secondary cause of glenohumeral osteoarthritis, inflammatory arthritis, connective tissue disease, prior contralateral TSA, and prior ipsilateral scapula, glenoid, and proximal humerus surgery. Ultimately, 24 patients were included in the study.
CT data were formatted for preoperative templating. The CT images of each patient’s scapula were uploaded into Materialise Interactive Medical Image Control System (Mimics) software. Mimics allows 3-D image rendering and editing from various imaging modalities and formats. The software was used to create the 3-D scapula models for templating. Prior studies have validated the anatomical precision of 3-D models created with Mimics.20
Mimics was also used to digitize in 3-D the glenoid components from the Bigliani-Flatow Shoulder System (Zimmer Biomet). Glenoid components of 3 different sizes (40 mm, 46 mm, 52 mm) were used. (The Bigliani glenoid component was digitized, as this implant system was used for primary TSA in all 24 patients.) Each glenoid component was traced in 3-D with a Gage 2000 coordinate-measuring machine (Brown & Sharpe) and was processed with custom software. The custom software, cited in previous work by our group,17 created the same coordinate system for each scapula based on anatomical reference points. These digitized 3-D images of glenoid components were uploaded with the digitized 3-D scapulae derived from patients’ CT scans to the Magics software. Magics allows for manipulation and interaction of multiple 3-D models by creating electronic stereolithography files that provide 3-D surface geometry.
Three fellowship-trained shoulder surgeons and 4 shoulder fellows templated the most appropriately sized glenoid component for each of the 24 patients. At the time of templating, the surgeon was blinded to the size of the glenoid implant used in the surgery. In Magics, each scapula was positioned in 3-D similar to how it would appear with the patient in the beach-chair position during surgery. In both study arms, surgeons selected the largest component that maximized the area of contact while avoiding peg penetration of the glenoid vault or component overhang. In addition, surgeons were instructed to correct glenoid version to as near neutral as possible with component positioning but were not permitted to remove glenoid bone stock to correct deformity. All surgeons based placement of the glenoid component on the patient’s actual bone stock and not on osteophytes, which are readily appreciable on 3-D CT.
In study arm 1, the 3-D view of the glenoid was restricted to the initial view in the beach-chair position. The surgeon then manipulated the 3-D glenoid component template across a single 2-D plane, either the superior-inferior plane or the anterior-posterior plane, over the surface of the 3-D glenoid (Figure 1).
In study arm 2, surgeons were permitted to rotate the 3-D glenoid template and scapula in any manner (Figure 2).
Interobserver agreement was determined by comparing prosthetic glenoid component size selection among all study surgeons, and intraobserver agreement was determined by comparing glenoid size selection during 2 sessions separated by at least 3 weeks.
After each trial, the order of patients’ scapula images was randomly rearranged to reduce recall bias. Kappa (κ) coefficients were calculated for interobserver and intraobserver agreement. Kappas ranged from −1.0 (least agreement) to +1.0 (complete agreement). A κ of 0 indicated an observer selection was equivalent to random chance. The level of agreement was categorized according to κ using a system described by Landis and Koch21 (Table 1).
Results
The group of 24 patients consisted of 15 men and 9 women. Mean age was 70.3 years (range, 56-88 years). Primary TSA was performed in 14 right shoulders and 10 left shoulders. Of the 24 patients, 20 (83%) had a 46-mm glenoid component implanted, 3 male patients had a 52-mm glenoid component implanted, and 1 female patient had a 40-mm glenoid component implanted.
Study Arm 1: Glenoid Templating Based on 2 df
In study arm 1, overall intraobserver agreement was substantial, as defined in the statistical literature.21 Among all surgeons who participated, intraobserver agreeement was 0.76 (substantial), 0.60 (substantial), and 0.58 (moderate) for the 40-mm, 46-mm, and 52-mm glenoid components, respectively (overall κ = 0.67, substantial agreement). Trial 1 interobserver agreement was 0.56 (moderate) (P < .001), 0.25 (fair) (P < .001), and 0.21 (fair) (P < .001) for the 40-mm, 46-mm, and 52-mm glenoid components, respectively (overall κ = 0.36, fair agreement) (P < .001), and trial 2 interobserver agreement was 0.58 (moderate) (P < .001), 0.18 (poor) (P = .003), and 0.24 (fair) (P <.001) for the 40-mm, 46-mm, and 52-mm glenoid components, respectively (overall κ = 0.32, fair agreement) (P < .001). In study arm 1, therefore, trials 1 and 2 both showed fair interobserver agreement.
Study Arm 2: Glenoid Templating Based on 6 df
In study arm 2, a mean correlation of 0.42 (moderate agreement) was found between glenoid component size in 3-D templating and the glenoid component size ultimately selected during surgery (Table 3).
In study arm 2, overall intraobserver agreement was moderate. Among all surgeons who participated, intraobserver agreement was 0.80 (excellent), 0.43 (moderate), and 0.47 (moderate) for the 40-mm, 46-mm, and 52-mm glenoid components, respectively (overall κ = 0.58, moderate agreement). Trial 1 interobserver agreement was 0.75 (substantial) (P < .001), 0.39 (fair) (P < .001), and 0.50 (moderate) (P < .001) for the 40-mm, 46-mm, and 52-mm glenoid components, respectively (overall κ = 0.54, moderate agreement) (P < .001), and trial 2 interobserver agreement was 0.66 (substantial) (P < .001), 0.28 (fair) (P = .003), and 0.40 (moderate) (P < .001) for the 40-mm, 46-mm, and 52-mm glenoid components, respectively (overall κ = 0.43, moderate agreement) (P < .001).
Discussion
Our results showed that 3-D glenoid templating had reproducible intraobserver and interobserver agreement. Overall intraobserver agreement was substantial (κ = 0.67) for study arm 1 and moderate (κ = 0.58) for study arm 2. Interobserver agreement was fair for trials 1 and 2 (κ = 0.36 and 0.32) in arm 1 and moderate for trials 1 and 2 (κ = 0.54 and 0.43) in arm 2.
Intraobserver and interobserver agreement values, particularly in study arm 2, which incorporated rotation (6 df), are consistent with values in commonly used classification systems, such as the Neer system for proximal humerus fractures, the Frykman system for distal radius fractures, and the King system for adolescent idiopathic scoliosis.22-30 Sidor and colleagues27 found overall interobserver agreement of 0.50 and overall intraobserver agreement of 0.66 for the Neer system, and Illarramendi and colleagues24 found overall interobserver agreement of 0.43 and overall intraobserver agreement of 0.61 for the Frykman system.
In study arm 2, overall interobserver and intraobserver agreement was moderate. A higher level of surgeon agreement is unlikely given the lack of well-defined parameters for determining glenoid component size. Therefore, glenoid size selection is largely a matter of surgeon preference. More research is needed to establish concrete guidelines for glenoid component size selection. Once guidelines are adopted, interobserver agreement in templating may increase.
In both study arms, the component that surgeons selected during templating tended to be smaller than the component they selected during surgery. In study arm 1, 32% of patients had a smaller component selected based on computer modeling, and 7% had a larger component selected. In study arm 2, the difference was narrower: 27% of patients had a smaller component selected during templating, and 16% had a larger component selected. A statistically significant difference (P < .001) in templated and implanted component sizes was found between men and women: Templated glenoid components were smaller than implanted components in 53% of women and larger than implanted components in 33% of men. Differences between templated and implanted components may be attributable to visualization differences. During templating, the entire glenoid can be visualized and the slightest peg penetration or component overhang detected; in contrast, during surgery, anatomical constraints preclude such a comprehensive assessment.
Differences in agreement between templated and implanted glenoid components suggest that the size of implanted components may not be ideal. In this study, the distribution of the templated glenoid sizes was much wider than that of the implanted glenoid sizes. During templating, each glenoid component can be definitively visualized and assessed for possible peg penetration and overhang. Visualization allows surgeons to base glenoid size selection solely on glenoid morphology, as opposed to factors such as patient sex and height. In addition, interobserver and intraobserver agreement values for the 40-mm glenoid component were considerably higher than those for components of other sizes, indicating that the 40-mm component was consistently and reproducibly selected for the same patients. Hence, templating may particularly help prevent peg penetration and component overhang for patients with a smaller diameter glenoid.
More research on 3-D templating is warranted given the results of this study and other studies.12,17,31 Scalise and colleagues31 found that, in TSA planning, surgeons’ use of 2-D (vs 3-D) imaging led them to overestimate glenoid component sizes (P = .006). In our study, the glenoid size selected during 3-D templating was, in many cases, smaller than the size selected during surgery. In order to avoid peg penetration and glenoid overhang, anecdotal guidelines commonly used in glenoid size selection, likely was the driving force in selecting smaller glenoid components during templating. Although anterior, superior, and inferior glenoid overhang typically can be assessed during surgery, posterior overhang is more difficult to evaluate. Three-dimensional modeling allows surgeons to determine optimal glenoid component size and position. In addition, intraoperative evaluation of glenoid component peg penetration is challenging, and peg penetration becomes evident only after it has occurred. During templating, however, surgeons were able to easily assess for peg penetration, and smaller glenoid components were selected.
A limitation of this study is that intraoperative glenoid version correction or peg containment was not quantified. More research is needed on the relationship between glenoid size selection and component overhang and peg penetration. Another limitation was use of only 1 TSA system (with 3 glenoid sizes, all with inline pegs); reliability of 3-D templating was not evaluated across different component designs. Last, given the absence of guidelines for glenoid component size selection, there was surgeon bias in preoperative templating and in intraoperative selection of glenoid size. Surgeons had differing opinions on the importance of maximizing the contact area of the component and correcting glenoid deformity and version.
Our study results showed that preoperative 3-D templating that allows for superior-inferior, anterior-posterior, and rotational translation was consistent and reproducible in determining glenoid component size, and use of this templating may reduce the risks of implant overhang, peg penetration, and decreased stability ratio. These results highlight the possibility that glenoid component sizes selected during surgery may not be ideal. More research is needed to determine if intraoperative glenoid size selection leads to adequate version correction and peg containment. The present study supports use of 3-D templating in primary TSA planning.
1. Neer CS 2nd. Replacement arthroplasty for glenohumeral osteoarthritis. J Bone Joint Surg Am. 1974;56(1):1-13.
2. Neer CS 2nd, Watson KC, Stanton FJ. Recent experience in total shoulder replacement. J Bone Joint Surg Am. 1982;64(3):319-337.
3. Day JS, Lau E, Ong KL, Williams GR, Ramsey ML, Kurtz SM. Prevalence and projections of total shoulder and elbow arthroplasty in the United States to 2015. J Shoulder Elbow Surg. 2010;19(8):1115-1120.
4. Torchia ME, Cofield RH, Settergren CR. Total shoulder arthroplasty with the Neer prosthesis: long-term results. J Shoulder Elbow Surg. 1997;6(6):495-505.
5. Barrett WP, Franklin JL, Jackins SE, Wyss CR, Matsen FA 3rd. Total shoulder arthroplasty. J Bone Joint Surg Am. 1987;69(6):865-872.
6. Bohsali KI, Wirth MA, Rockwood CA Jr. Complications of total shoulder arthroplasty. J Bone Joint Surg Am. 2006;88(10):2279-2292.
7. Matsen FA 3rd, Bicknell RT, Lippitt SB. Shoulder arthroplasty: the socket perspective. J Shoulder Elbow Surg. 2007;16(5 suppl):S241-S247.
8. Matsen FA 3rd, Clinton J, Lynch J, Bertelsen A, Richardson ML. Glenoid component failure in total shoulder arthroplasty. J Bone Joint Surg Am. 2008;90(4):885-896.
9. Pearl ML, Romeo AA, Wirth MA, Yamaguchi K, Nicholson GP, Creighton RA. Decision making in contemporary shoulder arthroplasty. Instr Course Lect. 2005;54:69-85.
10. Wirth MA, Rockwood CA Jr. Complications of total shoulder-replacement arthroplasty. J Bone Joint Surg Am. 1996;78(4):603-616.
11. Sanchez-Sotelo J, Sperling JW, Rowland CM, Cofield RH. Instability after shoulder arthroplasty: results of surgical treatment. J Bone Joint Surg Am. 2003;85(4):622-631.
12. Tammachote N, Sperling JW, Berglund LJ, Steinmann SP, Cofield RH, An KN. The effect of glenoid component size on the stability of total shoulder arthroplasty. J Shoulder Elbow Surg. 2007;16(3 suppl):S102-S106.
13. Iannotti JP, Greeson C, Downing D, Sabesan V, Bryan JA. Effect of glenoid deformity on glenoid component placement in primary shoulder arthroplasty. J Shoulder Elbow Surg. 2012;21(1):48-55.
14. Briem D, Ruecker AH, Neumann J, et al. 3D fluoroscopic navigated reaming of the glenoid for total shoulder arthroplasty (TSA). Comput Aided Surg. 2011;16(2):93-99.
15. Budge MD, Lewis GS, Schaefer E, Coquia S, Flemming DJ, Armstrong AD. Comparison of standard two-dimensional and three-dimensional corrected glenoid version measurements. J Shoulder Elbow Surg. 2011;20(4):577-583.
16. Chuang TY, Adams CR, Burkhart SS. Use of preoperative three-dimensional computed tomography to quantify glenoid bone loss in shoulder instability. Arthroscopy. 2008;24(4):376-382.
17. Nowak DD, Bahu MJ, Gardner TR, et al. Simulation of surgical glenoid resurfacing using three-dimensional computed tomography of the arthritic glenohumeral joint: the amount of glenoid retroversion that can be corrected. J Shoulder Elbow Surg. 2009;18(5):680-688.
18. Scalise JJ, Bryan J, Polster J, Brems JJ, Iannotti JP. Quantitative analysis of glenoid bone loss in osteoarthritis using three-dimensional computed tomography scans. J Shoulder Elbow Surg. 2008;17(2):328-335.
19. Scalise JJ, Codsi MJ, Bryan J, Iannotti JP. The three-dimensional glenoid vault model can estimate normal glenoid version in osteoarthritis. J Shoulder Elbow Surg. 2008;17(3):487-491.
20. Bryce CD, Pennypacker JL, Kulkarni N, et al. Validation of three-dimensional models of in situ scapulae. J Shoulder Elbow Surg. 2008;17(5):825-832.
21. Landis JR, Koch GG. The measurement of observer agreement for categorical data. Biometrics. 1977;33(1):159-174.
22. Cummings RJ, Loveless EA, Campbell J, Samelson S, Mazur JM. Interobserver reliability and intraobserver reproducibility of the system of King et al. for the classification of adolescent idiopathic scoliosis. J Bone Joint Surg Am. 1998;80(8):1107-1111.
23. Humphrey CA, Dirschl DR, Ellis TJ. Interobserver reliability of a CT-based fracture classification system. J Orthop Trauma. 2005;19(9):616-622.
24. Illarramendi A, González Della Valle A, Segal E, De Carli P, Maignon G, Gallucci G. Evaluation of simplified Frykman and AO classifications of fractures of the distal radius. Assessment of interobserver and intraobserver agreement. Int Orthop. 1998;22(2):111-115.
25. Lenke LG, Betz RR, Bridwell KH, et al. Intraobserver and interobserver reliability of the classification of thoracic adolescent idiopathic scoliosis. J Bone Joint Surg Am. 1998;80(8):1097-1106.
26. Ploegmakers JJ, Mader K, Pennig D, Verheyen CC. Four distal radial fracture classification systems tested amongst a large panel of Dutch trauma surgeons. Injury. 2007;38(11):1268-1272.
27. Sidor ML, Zuckerman JD, Lyon T, Koval K, Cuomo F, Schoenberg N. The Neer classification system for proximal humeral fractures. An assessment of interobserver reliability and intraobserver reproducibility. J Bone Joint Surg Am. 1993;75(12):1745-1750.
28. Siebenrock KA, Gerber C. The reproducibility of classification of fractures of the proximal end of the humerus. J Bone Joint Surg Am. 1993;75(12):1751-1755.
29. Thomsen NO, Overgaard S, Olsen LH, Hansen H, Nielsen ST. Observer variation in the radiographic classification of ankle fractures. J Bone Joint Surg Br. 1991;73(4):676-678.
30. Ward WT, Vogt M, Grudziak JS, Tümer Y, Cook PC, Fitch RD. Severin classification system for evaluation of the results of operative treatment of congenital dislocation of the hip. A study of intraobserver and interobserver reliability. J Bone Joint Surg Am. 1997;79(5):656-663.
31. Scalise JJ, Codsi MJ, Bryan J, Brems JJ, Iannotti JP. The influence of three-dimensional computed tomography images of the shoulder in preoperative planning for total shoulder arthroplasty. J Bone Joint Surg Am. 2008;90(11):2438-2445.
Take-Home Points
- Guidelines regarding glenoid component size selection for primary TSA are lacking.
- Intraoperative in situ glenoid sizing may not be ideal.
- 3-D digital models may be utilized for preoperative templating of glenoid component size in primary TSA.
- 3-D templating that allows for superior-inferior, anterior-posterior, and rotational translation can lead to consistent and reproducible templating of glenoid component size.
- 3-D templating may reduce the risks of implant overhang, peg penetration, and decreased stability ratio.
In 1974, Neer1 introduced the shoulder prosthesis. In 1982, Neer and colleagues2 found significant improvement in shoulder pain and function in patients with glenohumeral osteoarthritis treated with the Neer prosthesis. Since then, use of total shoulder arthroplasty (TSA) has increased. Between 1993 and 2007, TSA use increased 319% in the United States.3 Long-term outcomes studies have found implant survivorship ranging from 87% to 93% at 10 to 15 years.4
Although TSA is a successful procedure, glenoid component failure is the most common complication.5-10 Outcomes of revision surgery for glenoid instability are inferior to those of primary TSA.11 Recent research findings highlight the effect of glenoid size on TSA complications.12 A larger glenoid component increases the stability ratio (peak subluxation force divided by compression load).12 However, insufficient glenoid bone stock, small glenoid diameter, and inability to fit a properly sized reamer owing to soft-tissue constraints may lead surgeons to choose a smaller glenoid component in order to avoid peg penetration, overhang, and soft-tissue damage, respectively. Therefore, preoperative templating of glenoid size is a potential strategy for minimizing complications.
Templating is performed for proximal humeral components, but glenoid sizing typically is deferred to intraoperative in situ sizing with implant-specific targeting guides. This glenoid sizing practice arose out of a lack of standard digital glenoid templates and difficulty in selecting glenoid size based on plain radiographs and/or 2-dimensional (2-D) computed tomography (CT) scans. However, targeting devices are sporadically used during surgery, and intraoperative glenoid vault dimension estimates derived from visualization and palpation are often inaccurate. Often, rather than directly assess glenoid morphology, surgeons infer glenoid size from the size and sex of patients.13
Three-dimensional (3-D) CT can be used to accurately assess glenoid version, bone loss, and implant fit.14-19 We conducted a study to determine if 3-D digital imaging can be consistently and reproducibly used for preoperative templating of glenoid component size and to determine if glenoid sizes derived from templating correlate with the sizes of subsequently implanted glenoids.
Materials and Methods
This retrospective study was conducted at the Center for Shoulder, Elbow, and Sports Medicine at Columbia University Medical Center in New York City and was approved by our Institutional Review Board. Included in the study were all patients who underwent primary TSA for primary glenohumeral osteoarthritis over a 12-month period. Patients were required to have preoperative CT performed according to our study protocol. The CT protocol consisted of 0.5-mm axial cuts of the entire scapula and 3-D reconstruction of the scapula, glenoid, glenohumeral articulation, and proximal humerus. Patients were excluded from the study for primary TSA for a secondary cause of glenohumeral osteoarthritis, inflammatory arthritis, connective tissue disease, prior contralateral TSA, and prior ipsilateral scapula, glenoid, and proximal humerus surgery. Ultimately, 24 patients were included in the study.
CT data were formatted for preoperative templating. The CT images of each patient’s scapula were uploaded into Materialise Interactive Medical Image Control System (Mimics) software. Mimics allows 3-D image rendering and editing from various imaging modalities and formats. The software was used to create the 3-D scapula models for templating. Prior studies have validated the anatomical precision of 3-D models created with Mimics.20
Mimics was also used to digitize in 3-D the glenoid components from the Bigliani-Flatow Shoulder System (Zimmer Biomet). Glenoid components of 3 different sizes (40 mm, 46 mm, 52 mm) were used. (The Bigliani glenoid component was digitized, as this implant system was used for primary TSA in all 24 patients.) Each glenoid component was traced in 3-D with a Gage 2000 coordinate-measuring machine (Brown & Sharpe) and was processed with custom software. The custom software, cited in previous work by our group,17 created the same coordinate system for each scapula based on anatomical reference points. These digitized 3-D images of glenoid components were uploaded with the digitized 3-D scapulae derived from patients’ CT scans to the Magics software. Magics allows for manipulation and interaction of multiple 3-D models by creating electronic stereolithography files that provide 3-D surface geometry.
Three fellowship-trained shoulder surgeons and 4 shoulder fellows templated the most appropriately sized glenoid component for each of the 24 patients. At the time of templating, the surgeon was blinded to the size of the glenoid implant used in the surgery. In Magics, each scapula was positioned in 3-D similar to how it would appear with the patient in the beach-chair position during surgery. In both study arms, surgeons selected the largest component that maximized the area of contact while avoiding peg penetration of the glenoid vault or component overhang. In addition, surgeons were instructed to correct glenoid version to as near neutral as possible with component positioning but were not permitted to remove glenoid bone stock to correct deformity. All surgeons based placement of the glenoid component on the patient’s actual bone stock and not on osteophytes, which are readily appreciable on 3-D CT.
In study arm 1, the 3-D view of the glenoid was restricted to the initial view in the beach-chair position. The surgeon then manipulated the 3-D glenoid component template across a single 2-D plane, either the superior-inferior plane or the anterior-posterior plane, over the surface of the 3-D glenoid (Figure 1).
In study arm 2, surgeons were permitted to rotate the 3-D glenoid template and scapula in any manner (Figure 2).
Interobserver agreement was determined by comparing prosthetic glenoid component size selection among all study surgeons, and intraobserver agreement was determined by comparing glenoid size selection during 2 sessions separated by at least 3 weeks.
After each trial, the order of patients’ scapula images was randomly rearranged to reduce recall bias. Kappa (κ) coefficients were calculated for interobserver and intraobserver agreement. Kappas ranged from −1.0 (least agreement) to +1.0 (complete agreement). A κ of 0 indicated an observer selection was equivalent to random chance. The level of agreement was categorized according to κ using a system described by Landis and Koch21 (Table 1).
Results
The group of 24 patients consisted of 15 men and 9 women. Mean age was 70.3 years (range, 56-88 years). Primary TSA was performed in 14 right shoulders and 10 left shoulders. Of the 24 patients, 20 (83%) had a 46-mm glenoid component implanted, 3 male patients had a 52-mm glenoid component implanted, and 1 female patient had a 40-mm glenoid component implanted.
Study Arm 1: Glenoid Templating Based on 2 df
In study arm 1, overall intraobserver agreement was substantial, as defined in the statistical literature.21 Among all surgeons who participated, intraobserver agreeement was 0.76 (substantial), 0.60 (substantial), and 0.58 (moderate) for the 40-mm, 46-mm, and 52-mm glenoid components, respectively (overall κ = 0.67, substantial agreement). Trial 1 interobserver agreement was 0.56 (moderate) (P < .001), 0.25 (fair) (P < .001), and 0.21 (fair) (P < .001) for the 40-mm, 46-mm, and 52-mm glenoid components, respectively (overall κ = 0.36, fair agreement) (P < .001), and trial 2 interobserver agreement was 0.58 (moderate) (P < .001), 0.18 (poor) (P = .003), and 0.24 (fair) (P <.001) for the 40-mm, 46-mm, and 52-mm glenoid components, respectively (overall κ = 0.32, fair agreement) (P < .001). In study arm 1, therefore, trials 1 and 2 both showed fair interobserver agreement.
Study Arm 2: Glenoid Templating Based on 6 df
In study arm 2, a mean correlation of 0.42 (moderate agreement) was found between glenoid component size in 3-D templating and the glenoid component size ultimately selected during surgery (Table 3).
In study arm 2, overall intraobserver agreement was moderate. Among all surgeons who participated, intraobserver agreement was 0.80 (excellent), 0.43 (moderate), and 0.47 (moderate) for the 40-mm, 46-mm, and 52-mm glenoid components, respectively (overall κ = 0.58, moderate agreement). Trial 1 interobserver agreement was 0.75 (substantial) (P < .001), 0.39 (fair) (P < .001), and 0.50 (moderate) (P < .001) for the 40-mm, 46-mm, and 52-mm glenoid components, respectively (overall κ = 0.54, moderate agreement) (P < .001), and trial 2 interobserver agreement was 0.66 (substantial) (P < .001), 0.28 (fair) (P = .003), and 0.40 (moderate) (P < .001) for the 40-mm, 46-mm, and 52-mm glenoid components, respectively (overall κ = 0.43, moderate agreement) (P < .001).
Discussion
Our results showed that 3-D glenoid templating had reproducible intraobserver and interobserver agreement. Overall intraobserver agreement was substantial (κ = 0.67) for study arm 1 and moderate (κ = 0.58) for study arm 2. Interobserver agreement was fair for trials 1 and 2 (κ = 0.36 and 0.32) in arm 1 and moderate for trials 1 and 2 (κ = 0.54 and 0.43) in arm 2.
Intraobserver and interobserver agreement values, particularly in study arm 2, which incorporated rotation (6 df), are consistent with values in commonly used classification systems, such as the Neer system for proximal humerus fractures, the Frykman system for distal radius fractures, and the King system for adolescent idiopathic scoliosis.22-30 Sidor and colleagues27 found overall interobserver agreement of 0.50 and overall intraobserver agreement of 0.66 for the Neer system, and Illarramendi and colleagues24 found overall interobserver agreement of 0.43 and overall intraobserver agreement of 0.61 for the Frykman system.
In study arm 2, overall interobserver and intraobserver agreement was moderate. A higher level of surgeon agreement is unlikely given the lack of well-defined parameters for determining glenoid component size. Therefore, glenoid size selection is largely a matter of surgeon preference. More research is needed to establish concrete guidelines for glenoid component size selection. Once guidelines are adopted, interobserver agreement in templating may increase.
In both study arms, the component that surgeons selected during templating tended to be smaller than the component they selected during surgery. In study arm 1, 32% of patients had a smaller component selected based on computer modeling, and 7% had a larger component selected. In study arm 2, the difference was narrower: 27% of patients had a smaller component selected during templating, and 16% had a larger component selected. A statistically significant difference (P < .001) in templated and implanted component sizes was found between men and women: Templated glenoid components were smaller than implanted components in 53% of women and larger than implanted components in 33% of men. Differences between templated and implanted components may be attributable to visualization differences. During templating, the entire glenoid can be visualized and the slightest peg penetration or component overhang detected; in contrast, during surgery, anatomical constraints preclude such a comprehensive assessment.
Differences in agreement between templated and implanted glenoid components suggest that the size of implanted components may not be ideal. In this study, the distribution of the templated glenoid sizes was much wider than that of the implanted glenoid sizes. During templating, each glenoid component can be definitively visualized and assessed for possible peg penetration and overhang. Visualization allows surgeons to base glenoid size selection solely on glenoid morphology, as opposed to factors such as patient sex and height. In addition, interobserver and intraobserver agreement values for the 40-mm glenoid component were considerably higher than those for components of other sizes, indicating that the 40-mm component was consistently and reproducibly selected for the same patients. Hence, templating may particularly help prevent peg penetration and component overhang for patients with a smaller diameter glenoid.
More research on 3-D templating is warranted given the results of this study and other studies.12,17,31 Scalise and colleagues31 found that, in TSA planning, surgeons’ use of 2-D (vs 3-D) imaging led them to overestimate glenoid component sizes (P = .006). In our study, the glenoid size selected during 3-D templating was, in many cases, smaller than the size selected during surgery. In order to avoid peg penetration and glenoid overhang, anecdotal guidelines commonly used in glenoid size selection, likely was the driving force in selecting smaller glenoid components during templating. Although anterior, superior, and inferior glenoid overhang typically can be assessed during surgery, posterior overhang is more difficult to evaluate. Three-dimensional modeling allows surgeons to determine optimal glenoid component size and position. In addition, intraoperative evaluation of glenoid component peg penetration is challenging, and peg penetration becomes evident only after it has occurred. During templating, however, surgeons were able to easily assess for peg penetration, and smaller glenoid components were selected.
A limitation of this study is that intraoperative glenoid version correction or peg containment was not quantified. More research is needed on the relationship between glenoid size selection and component overhang and peg penetration. Another limitation was use of only 1 TSA system (with 3 glenoid sizes, all with inline pegs); reliability of 3-D templating was not evaluated across different component designs. Last, given the absence of guidelines for glenoid component size selection, there was surgeon bias in preoperative templating and in intraoperative selection of glenoid size. Surgeons had differing opinions on the importance of maximizing the contact area of the component and correcting glenoid deformity and version.
Our study results showed that preoperative 3-D templating that allows for superior-inferior, anterior-posterior, and rotational translation was consistent and reproducible in determining glenoid component size, and use of this templating may reduce the risks of implant overhang, peg penetration, and decreased stability ratio. These results highlight the possibility that glenoid component sizes selected during surgery may not be ideal. More research is needed to determine if intraoperative glenoid size selection leads to adequate version correction and peg containment. The present study supports use of 3-D templating in primary TSA planning.
Take-Home Points
- Guidelines regarding glenoid component size selection for primary TSA are lacking.
- Intraoperative in situ glenoid sizing may not be ideal.
- 3-D digital models may be utilized for preoperative templating of glenoid component size in primary TSA.
- 3-D templating that allows for superior-inferior, anterior-posterior, and rotational translation can lead to consistent and reproducible templating of glenoid component size.
- 3-D templating may reduce the risks of implant overhang, peg penetration, and decreased stability ratio.
In 1974, Neer1 introduced the shoulder prosthesis. In 1982, Neer and colleagues2 found significant improvement in shoulder pain and function in patients with glenohumeral osteoarthritis treated with the Neer prosthesis. Since then, use of total shoulder arthroplasty (TSA) has increased. Between 1993 and 2007, TSA use increased 319% in the United States.3 Long-term outcomes studies have found implant survivorship ranging from 87% to 93% at 10 to 15 years.4
Although TSA is a successful procedure, glenoid component failure is the most common complication.5-10 Outcomes of revision surgery for glenoid instability are inferior to those of primary TSA.11 Recent research findings highlight the effect of glenoid size on TSA complications.12 A larger glenoid component increases the stability ratio (peak subluxation force divided by compression load).12 However, insufficient glenoid bone stock, small glenoid diameter, and inability to fit a properly sized reamer owing to soft-tissue constraints may lead surgeons to choose a smaller glenoid component in order to avoid peg penetration, overhang, and soft-tissue damage, respectively. Therefore, preoperative templating of glenoid size is a potential strategy for minimizing complications.
Templating is performed for proximal humeral components, but glenoid sizing typically is deferred to intraoperative in situ sizing with implant-specific targeting guides. This glenoid sizing practice arose out of a lack of standard digital glenoid templates and difficulty in selecting glenoid size based on plain radiographs and/or 2-dimensional (2-D) computed tomography (CT) scans. However, targeting devices are sporadically used during surgery, and intraoperative glenoid vault dimension estimates derived from visualization and palpation are often inaccurate. Often, rather than directly assess glenoid morphology, surgeons infer glenoid size from the size and sex of patients.13
Three-dimensional (3-D) CT can be used to accurately assess glenoid version, bone loss, and implant fit.14-19 We conducted a study to determine if 3-D digital imaging can be consistently and reproducibly used for preoperative templating of glenoid component size and to determine if glenoid sizes derived from templating correlate with the sizes of subsequently implanted glenoids.
Materials and Methods
This retrospective study was conducted at the Center for Shoulder, Elbow, and Sports Medicine at Columbia University Medical Center in New York City and was approved by our Institutional Review Board. Included in the study were all patients who underwent primary TSA for primary glenohumeral osteoarthritis over a 12-month period. Patients were required to have preoperative CT performed according to our study protocol. The CT protocol consisted of 0.5-mm axial cuts of the entire scapula and 3-D reconstruction of the scapula, glenoid, glenohumeral articulation, and proximal humerus. Patients were excluded from the study for primary TSA for a secondary cause of glenohumeral osteoarthritis, inflammatory arthritis, connective tissue disease, prior contralateral TSA, and prior ipsilateral scapula, glenoid, and proximal humerus surgery. Ultimately, 24 patients were included in the study.
CT data were formatted for preoperative templating. The CT images of each patient’s scapula were uploaded into Materialise Interactive Medical Image Control System (Mimics) software. Mimics allows 3-D image rendering and editing from various imaging modalities and formats. The software was used to create the 3-D scapula models for templating. Prior studies have validated the anatomical precision of 3-D models created with Mimics.20
Mimics was also used to digitize in 3-D the glenoid components from the Bigliani-Flatow Shoulder System (Zimmer Biomet). Glenoid components of 3 different sizes (40 mm, 46 mm, 52 mm) were used. (The Bigliani glenoid component was digitized, as this implant system was used for primary TSA in all 24 patients.) Each glenoid component was traced in 3-D with a Gage 2000 coordinate-measuring machine (Brown & Sharpe) and was processed with custom software. The custom software, cited in previous work by our group,17 created the same coordinate system for each scapula based on anatomical reference points. These digitized 3-D images of glenoid components were uploaded with the digitized 3-D scapulae derived from patients’ CT scans to the Magics software. Magics allows for manipulation and interaction of multiple 3-D models by creating electronic stereolithography files that provide 3-D surface geometry.
Three fellowship-trained shoulder surgeons and 4 shoulder fellows templated the most appropriately sized glenoid component for each of the 24 patients. At the time of templating, the surgeon was blinded to the size of the glenoid implant used in the surgery. In Magics, each scapula was positioned in 3-D similar to how it would appear with the patient in the beach-chair position during surgery. In both study arms, surgeons selected the largest component that maximized the area of contact while avoiding peg penetration of the glenoid vault or component overhang. In addition, surgeons were instructed to correct glenoid version to as near neutral as possible with component positioning but were not permitted to remove glenoid bone stock to correct deformity. All surgeons based placement of the glenoid component on the patient’s actual bone stock and not on osteophytes, which are readily appreciable on 3-D CT.
In study arm 1, the 3-D view of the glenoid was restricted to the initial view in the beach-chair position. The surgeon then manipulated the 3-D glenoid component template across a single 2-D plane, either the superior-inferior plane or the anterior-posterior plane, over the surface of the 3-D glenoid (Figure 1).
In study arm 2, surgeons were permitted to rotate the 3-D glenoid template and scapula in any manner (Figure 2).
Interobserver agreement was determined by comparing prosthetic glenoid component size selection among all study surgeons, and intraobserver agreement was determined by comparing glenoid size selection during 2 sessions separated by at least 3 weeks.
After each trial, the order of patients’ scapula images was randomly rearranged to reduce recall bias. Kappa (κ) coefficients were calculated for interobserver and intraobserver agreement. Kappas ranged from −1.0 (least agreement) to +1.0 (complete agreement). A κ of 0 indicated an observer selection was equivalent to random chance. The level of agreement was categorized according to κ using a system described by Landis and Koch21 (Table 1).
Results
The group of 24 patients consisted of 15 men and 9 women. Mean age was 70.3 years (range, 56-88 years). Primary TSA was performed in 14 right shoulders and 10 left shoulders. Of the 24 patients, 20 (83%) had a 46-mm glenoid component implanted, 3 male patients had a 52-mm glenoid component implanted, and 1 female patient had a 40-mm glenoid component implanted.
Study Arm 1: Glenoid Templating Based on 2 df
In study arm 1, overall intraobserver agreement was substantial, as defined in the statistical literature.21 Among all surgeons who participated, intraobserver agreeement was 0.76 (substantial), 0.60 (substantial), and 0.58 (moderate) for the 40-mm, 46-mm, and 52-mm glenoid components, respectively (overall κ = 0.67, substantial agreement). Trial 1 interobserver agreement was 0.56 (moderate) (P < .001), 0.25 (fair) (P < .001), and 0.21 (fair) (P < .001) for the 40-mm, 46-mm, and 52-mm glenoid components, respectively (overall κ = 0.36, fair agreement) (P < .001), and trial 2 interobserver agreement was 0.58 (moderate) (P < .001), 0.18 (poor) (P = .003), and 0.24 (fair) (P <.001) for the 40-mm, 46-mm, and 52-mm glenoid components, respectively (overall κ = 0.32, fair agreement) (P < .001). In study arm 1, therefore, trials 1 and 2 both showed fair interobserver agreement.
Study Arm 2: Glenoid Templating Based on 6 df
In study arm 2, a mean correlation of 0.42 (moderate agreement) was found between glenoid component size in 3-D templating and the glenoid component size ultimately selected during surgery (Table 3).
In study arm 2, overall intraobserver agreement was moderate. Among all surgeons who participated, intraobserver agreement was 0.80 (excellent), 0.43 (moderate), and 0.47 (moderate) for the 40-mm, 46-mm, and 52-mm glenoid components, respectively (overall κ = 0.58, moderate agreement). Trial 1 interobserver agreement was 0.75 (substantial) (P < .001), 0.39 (fair) (P < .001), and 0.50 (moderate) (P < .001) for the 40-mm, 46-mm, and 52-mm glenoid components, respectively (overall κ = 0.54, moderate agreement) (P < .001), and trial 2 interobserver agreement was 0.66 (substantial) (P < .001), 0.28 (fair) (P = .003), and 0.40 (moderate) (P < .001) for the 40-mm, 46-mm, and 52-mm glenoid components, respectively (overall κ = 0.43, moderate agreement) (P < .001).
Discussion
Our results showed that 3-D glenoid templating had reproducible intraobserver and interobserver agreement. Overall intraobserver agreement was substantial (κ = 0.67) for study arm 1 and moderate (κ = 0.58) for study arm 2. Interobserver agreement was fair for trials 1 and 2 (κ = 0.36 and 0.32) in arm 1 and moderate for trials 1 and 2 (κ = 0.54 and 0.43) in arm 2.
Intraobserver and interobserver agreement values, particularly in study arm 2, which incorporated rotation (6 df), are consistent with values in commonly used classification systems, such as the Neer system for proximal humerus fractures, the Frykman system for distal radius fractures, and the King system for adolescent idiopathic scoliosis.22-30 Sidor and colleagues27 found overall interobserver agreement of 0.50 and overall intraobserver agreement of 0.66 for the Neer system, and Illarramendi and colleagues24 found overall interobserver agreement of 0.43 and overall intraobserver agreement of 0.61 for the Frykman system.
In study arm 2, overall interobserver and intraobserver agreement was moderate. A higher level of surgeon agreement is unlikely given the lack of well-defined parameters for determining glenoid component size. Therefore, glenoid size selection is largely a matter of surgeon preference. More research is needed to establish concrete guidelines for glenoid component size selection. Once guidelines are adopted, interobserver agreement in templating may increase.
In both study arms, the component that surgeons selected during templating tended to be smaller than the component they selected during surgery. In study arm 1, 32% of patients had a smaller component selected based on computer modeling, and 7% had a larger component selected. In study arm 2, the difference was narrower: 27% of patients had a smaller component selected during templating, and 16% had a larger component selected. A statistically significant difference (P < .001) in templated and implanted component sizes was found between men and women: Templated glenoid components were smaller than implanted components in 53% of women and larger than implanted components in 33% of men. Differences between templated and implanted components may be attributable to visualization differences. During templating, the entire glenoid can be visualized and the slightest peg penetration or component overhang detected; in contrast, during surgery, anatomical constraints preclude such a comprehensive assessment.
Differences in agreement between templated and implanted glenoid components suggest that the size of implanted components may not be ideal. In this study, the distribution of the templated glenoid sizes was much wider than that of the implanted glenoid sizes. During templating, each glenoid component can be definitively visualized and assessed for possible peg penetration and overhang. Visualization allows surgeons to base glenoid size selection solely on glenoid morphology, as opposed to factors such as patient sex and height. In addition, interobserver and intraobserver agreement values for the 40-mm glenoid component were considerably higher than those for components of other sizes, indicating that the 40-mm component was consistently and reproducibly selected for the same patients. Hence, templating may particularly help prevent peg penetration and component overhang for patients with a smaller diameter glenoid.
More research on 3-D templating is warranted given the results of this study and other studies.12,17,31 Scalise and colleagues31 found that, in TSA planning, surgeons’ use of 2-D (vs 3-D) imaging led them to overestimate glenoid component sizes (P = .006). In our study, the glenoid size selected during 3-D templating was, in many cases, smaller than the size selected during surgery. In order to avoid peg penetration and glenoid overhang, anecdotal guidelines commonly used in glenoid size selection, likely was the driving force in selecting smaller glenoid components during templating. Although anterior, superior, and inferior glenoid overhang typically can be assessed during surgery, posterior overhang is more difficult to evaluate. Three-dimensional modeling allows surgeons to determine optimal glenoid component size and position. In addition, intraoperative evaluation of glenoid component peg penetration is challenging, and peg penetration becomes evident only after it has occurred. During templating, however, surgeons were able to easily assess for peg penetration, and smaller glenoid components were selected.
A limitation of this study is that intraoperative glenoid version correction or peg containment was not quantified. More research is needed on the relationship between glenoid size selection and component overhang and peg penetration. Another limitation was use of only 1 TSA system (with 3 glenoid sizes, all with inline pegs); reliability of 3-D templating was not evaluated across different component designs. Last, given the absence of guidelines for glenoid component size selection, there was surgeon bias in preoperative templating and in intraoperative selection of glenoid size. Surgeons had differing opinions on the importance of maximizing the contact area of the component and correcting glenoid deformity and version.
Our study results showed that preoperative 3-D templating that allows for superior-inferior, anterior-posterior, and rotational translation was consistent and reproducible in determining glenoid component size, and use of this templating may reduce the risks of implant overhang, peg penetration, and decreased stability ratio. These results highlight the possibility that glenoid component sizes selected during surgery may not be ideal. More research is needed to determine if intraoperative glenoid size selection leads to adequate version correction and peg containment. The present study supports use of 3-D templating in primary TSA planning.
1. Neer CS 2nd. Replacement arthroplasty for glenohumeral osteoarthritis. J Bone Joint Surg Am. 1974;56(1):1-13.
2. Neer CS 2nd, Watson KC, Stanton FJ. Recent experience in total shoulder replacement. J Bone Joint Surg Am. 1982;64(3):319-337.
3. Day JS, Lau E, Ong KL, Williams GR, Ramsey ML, Kurtz SM. Prevalence and projections of total shoulder and elbow arthroplasty in the United States to 2015. J Shoulder Elbow Surg. 2010;19(8):1115-1120.
4. Torchia ME, Cofield RH, Settergren CR. Total shoulder arthroplasty with the Neer prosthesis: long-term results. J Shoulder Elbow Surg. 1997;6(6):495-505.
5. Barrett WP, Franklin JL, Jackins SE, Wyss CR, Matsen FA 3rd. Total shoulder arthroplasty. J Bone Joint Surg Am. 1987;69(6):865-872.
6. Bohsali KI, Wirth MA, Rockwood CA Jr. Complications of total shoulder arthroplasty. J Bone Joint Surg Am. 2006;88(10):2279-2292.
7. Matsen FA 3rd, Bicknell RT, Lippitt SB. Shoulder arthroplasty: the socket perspective. J Shoulder Elbow Surg. 2007;16(5 suppl):S241-S247.
8. Matsen FA 3rd, Clinton J, Lynch J, Bertelsen A, Richardson ML. Glenoid component failure in total shoulder arthroplasty. J Bone Joint Surg Am. 2008;90(4):885-896.
9. Pearl ML, Romeo AA, Wirth MA, Yamaguchi K, Nicholson GP, Creighton RA. Decision making in contemporary shoulder arthroplasty. Instr Course Lect. 2005;54:69-85.
10. Wirth MA, Rockwood CA Jr. Complications of total shoulder-replacement arthroplasty. J Bone Joint Surg Am. 1996;78(4):603-616.
11. Sanchez-Sotelo J, Sperling JW, Rowland CM, Cofield RH. Instability after shoulder arthroplasty: results of surgical treatment. J Bone Joint Surg Am. 2003;85(4):622-631.
12. Tammachote N, Sperling JW, Berglund LJ, Steinmann SP, Cofield RH, An KN. The effect of glenoid component size on the stability of total shoulder arthroplasty. J Shoulder Elbow Surg. 2007;16(3 suppl):S102-S106.
13. Iannotti JP, Greeson C, Downing D, Sabesan V, Bryan JA. Effect of glenoid deformity on glenoid component placement in primary shoulder arthroplasty. J Shoulder Elbow Surg. 2012;21(1):48-55.
14. Briem D, Ruecker AH, Neumann J, et al. 3D fluoroscopic navigated reaming of the glenoid for total shoulder arthroplasty (TSA). Comput Aided Surg. 2011;16(2):93-99.
15. Budge MD, Lewis GS, Schaefer E, Coquia S, Flemming DJ, Armstrong AD. Comparison of standard two-dimensional and three-dimensional corrected glenoid version measurements. J Shoulder Elbow Surg. 2011;20(4):577-583.
16. Chuang TY, Adams CR, Burkhart SS. Use of preoperative three-dimensional computed tomography to quantify glenoid bone loss in shoulder instability. Arthroscopy. 2008;24(4):376-382.
17. Nowak DD, Bahu MJ, Gardner TR, et al. Simulation of surgical glenoid resurfacing using three-dimensional computed tomography of the arthritic glenohumeral joint: the amount of glenoid retroversion that can be corrected. J Shoulder Elbow Surg. 2009;18(5):680-688.
18. Scalise JJ, Bryan J, Polster J, Brems JJ, Iannotti JP. Quantitative analysis of glenoid bone loss in osteoarthritis using three-dimensional computed tomography scans. J Shoulder Elbow Surg. 2008;17(2):328-335.
19. Scalise JJ, Codsi MJ, Bryan J, Iannotti JP. The three-dimensional glenoid vault model can estimate normal glenoid version in osteoarthritis. J Shoulder Elbow Surg. 2008;17(3):487-491.
20. Bryce CD, Pennypacker JL, Kulkarni N, et al. Validation of three-dimensional models of in situ scapulae. J Shoulder Elbow Surg. 2008;17(5):825-832.
21. Landis JR, Koch GG. The measurement of observer agreement for categorical data. Biometrics. 1977;33(1):159-174.
22. Cummings RJ, Loveless EA, Campbell J, Samelson S, Mazur JM. Interobserver reliability and intraobserver reproducibility of the system of King et al. for the classification of adolescent idiopathic scoliosis. J Bone Joint Surg Am. 1998;80(8):1107-1111.
23. Humphrey CA, Dirschl DR, Ellis TJ. Interobserver reliability of a CT-based fracture classification system. J Orthop Trauma. 2005;19(9):616-622.
24. Illarramendi A, González Della Valle A, Segal E, De Carli P, Maignon G, Gallucci G. Evaluation of simplified Frykman and AO classifications of fractures of the distal radius. Assessment of interobserver and intraobserver agreement. Int Orthop. 1998;22(2):111-115.
25. Lenke LG, Betz RR, Bridwell KH, et al. Intraobserver and interobserver reliability of the classification of thoracic adolescent idiopathic scoliosis. J Bone Joint Surg Am. 1998;80(8):1097-1106.
26. Ploegmakers JJ, Mader K, Pennig D, Verheyen CC. Four distal radial fracture classification systems tested amongst a large panel of Dutch trauma surgeons. Injury. 2007;38(11):1268-1272.
27. Sidor ML, Zuckerman JD, Lyon T, Koval K, Cuomo F, Schoenberg N. The Neer classification system for proximal humeral fractures. An assessment of interobserver reliability and intraobserver reproducibility. J Bone Joint Surg Am. 1993;75(12):1745-1750.
28. Siebenrock KA, Gerber C. The reproducibility of classification of fractures of the proximal end of the humerus. J Bone Joint Surg Am. 1993;75(12):1751-1755.
29. Thomsen NO, Overgaard S, Olsen LH, Hansen H, Nielsen ST. Observer variation in the radiographic classification of ankle fractures. J Bone Joint Surg Br. 1991;73(4):676-678.
30. Ward WT, Vogt M, Grudziak JS, Tümer Y, Cook PC, Fitch RD. Severin classification system for evaluation of the results of operative treatment of congenital dislocation of the hip. A study of intraobserver and interobserver reliability. J Bone Joint Surg Am. 1997;79(5):656-663.
31. Scalise JJ, Codsi MJ, Bryan J, Brems JJ, Iannotti JP. The influence of three-dimensional computed tomography images of the shoulder in preoperative planning for total shoulder arthroplasty. J Bone Joint Surg Am. 2008;90(11):2438-2445.
1. Neer CS 2nd. Replacement arthroplasty for glenohumeral osteoarthritis. J Bone Joint Surg Am. 1974;56(1):1-13.
2. Neer CS 2nd, Watson KC, Stanton FJ. Recent experience in total shoulder replacement. J Bone Joint Surg Am. 1982;64(3):319-337.
3. Day JS, Lau E, Ong KL, Williams GR, Ramsey ML, Kurtz SM. Prevalence and projections of total shoulder and elbow arthroplasty in the United States to 2015. J Shoulder Elbow Surg. 2010;19(8):1115-1120.
4. Torchia ME, Cofield RH, Settergren CR. Total shoulder arthroplasty with the Neer prosthesis: long-term results. J Shoulder Elbow Surg. 1997;6(6):495-505.
5. Barrett WP, Franklin JL, Jackins SE, Wyss CR, Matsen FA 3rd. Total shoulder arthroplasty. J Bone Joint Surg Am. 1987;69(6):865-872.
6. Bohsali KI, Wirth MA, Rockwood CA Jr. Complications of total shoulder arthroplasty. J Bone Joint Surg Am. 2006;88(10):2279-2292.
7. Matsen FA 3rd, Bicknell RT, Lippitt SB. Shoulder arthroplasty: the socket perspective. J Shoulder Elbow Surg. 2007;16(5 suppl):S241-S247.
8. Matsen FA 3rd, Clinton J, Lynch J, Bertelsen A, Richardson ML. Glenoid component failure in total shoulder arthroplasty. J Bone Joint Surg Am. 2008;90(4):885-896.
9. Pearl ML, Romeo AA, Wirth MA, Yamaguchi K, Nicholson GP, Creighton RA. Decision making in contemporary shoulder arthroplasty. Instr Course Lect. 2005;54:69-85.
10. Wirth MA, Rockwood CA Jr. Complications of total shoulder-replacement arthroplasty. J Bone Joint Surg Am. 1996;78(4):603-616.
11. Sanchez-Sotelo J, Sperling JW, Rowland CM, Cofield RH. Instability after shoulder arthroplasty: results of surgical treatment. J Bone Joint Surg Am. 2003;85(4):622-631.
12. Tammachote N, Sperling JW, Berglund LJ, Steinmann SP, Cofield RH, An KN. The effect of glenoid component size on the stability of total shoulder arthroplasty. J Shoulder Elbow Surg. 2007;16(3 suppl):S102-S106.
13. Iannotti JP, Greeson C, Downing D, Sabesan V, Bryan JA. Effect of glenoid deformity on glenoid component placement in primary shoulder arthroplasty. J Shoulder Elbow Surg. 2012;21(1):48-55.
14. Briem D, Ruecker AH, Neumann J, et al. 3D fluoroscopic navigated reaming of the glenoid for total shoulder arthroplasty (TSA). Comput Aided Surg. 2011;16(2):93-99.
15. Budge MD, Lewis GS, Schaefer E, Coquia S, Flemming DJ, Armstrong AD. Comparison of standard two-dimensional and three-dimensional corrected glenoid version measurements. J Shoulder Elbow Surg. 2011;20(4):577-583.
16. Chuang TY, Adams CR, Burkhart SS. Use of preoperative three-dimensional computed tomography to quantify glenoid bone loss in shoulder instability. Arthroscopy. 2008;24(4):376-382.
17. Nowak DD, Bahu MJ, Gardner TR, et al. Simulation of surgical glenoid resurfacing using three-dimensional computed tomography of the arthritic glenohumeral joint: the amount of glenoid retroversion that can be corrected. J Shoulder Elbow Surg. 2009;18(5):680-688.
18. Scalise JJ, Bryan J, Polster J, Brems JJ, Iannotti JP. Quantitative analysis of glenoid bone loss in osteoarthritis using three-dimensional computed tomography scans. J Shoulder Elbow Surg. 2008;17(2):328-335.
19. Scalise JJ, Codsi MJ, Bryan J, Iannotti JP. The three-dimensional glenoid vault model can estimate normal glenoid version in osteoarthritis. J Shoulder Elbow Surg. 2008;17(3):487-491.
20. Bryce CD, Pennypacker JL, Kulkarni N, et al. Validation of three-dimensional models of in situ scapulae. J Shoulder Elbow Surg. 2008;17(5):825-832.
21. Landis JR, Koch GG. The measurement of observer agreement for categorical data. Biometrics. 1977;33(1):159-174.
22. Cummings RJ, Loveless EA, Campbell J, Samelson S, Mazur JM. Interobserver reliability and intraobserver reproducibility of the system of King et al. for the classification of adolescent idiopathic scoliosis. J Bone Joint Surg Am. 1998;80(8):1107-1111.
23. Humphrey CA, Dirschl DR, Ellis TJ. Interobserver reliability of a CT-based fracture classification system. J Orthop Trauma. 2005;19(9):616-622.
24. Illarramendi A, González Della Valle A, Segal E, De Carli P, Maignon G, Gallucci G. Evaluation of simplified Frykman and AO classifications of fractures of the distal radius. Assessment of interobserver and intraobserver agreement. Int Orthop. 1998;22(2):111-115.
25. Lenke LG, Betz RR, Bridwell KH, et al. Intraobserver and interobserver reliability of the classification of thoracic adolescent idiopathic scoliosis. J Bone Joint Surg Am. 1998;80(8):1097-1106.
26. Ploegmakers JJ, Mader K, Pennig D, Verheyen CC. Four distal radial fracture classification systems tested amongst a large panel of Dutch trauma surgeons. Injury. 2007;38(11):1268-1272.
27. Sidor ML, Zuckerman JD, Lyon T, Koval K, Cuomo F, Schoenberg N. The Neer classification system for proximal humeral fractures. An assessment of interobserver reliability and intraobserver reproducibility. J Bone Joint Surg Am. 1993;75(12):1745-1750.
28. Siebenrock KA, Gerber C. The reproducibility of classification of fractures of the proximal end of the humerus. J Bone Joint Surg Am. 1993;75(12):1751-1755.
29. Thomsen NO, Overgaard S, Olsen LH, Hansen H, Nielsen ST. Observer variation in the radiographic classification of ankle fractures. J Bone Joint Surg Br. 1991;73(4):676-678.
30. Ward WT, Vogt M, Grudziak JS, Tümer Y, Cook PC, Fitch RD. Severin classification system for evaluation of the results of operative treatment of congenital dislocation of the hip. A study of intraobserver and interobserver reliability. J Bone Joint Surg Am. 1997;79(5):656-663.
31. Scalise JJ, Codsi MJ, Bryan J, Brems JJ, Iannotti JP. The influence of three-dimensional computed tomography images of the shoulder in preoperative planning for total shoulder arthroplasty. J Bone Joint Surg Am. 2008;90(11):2438-2445.